(Review cs231n)loss function and optimization
分类器需要在识别物体变化时候具有很好的鲁棒性(robus)
线性分类器(linear classifier)理解为模板的匹配,根据数量,表达能力不足,泛化性低;理解为将图片看做在高维度区域
线性分类器对这个区域进行染色。
loss function 衡量预测结果的不理性程度,并基于损失函数优化weight, 使损失函数最小,达到在训练集的理想结果。
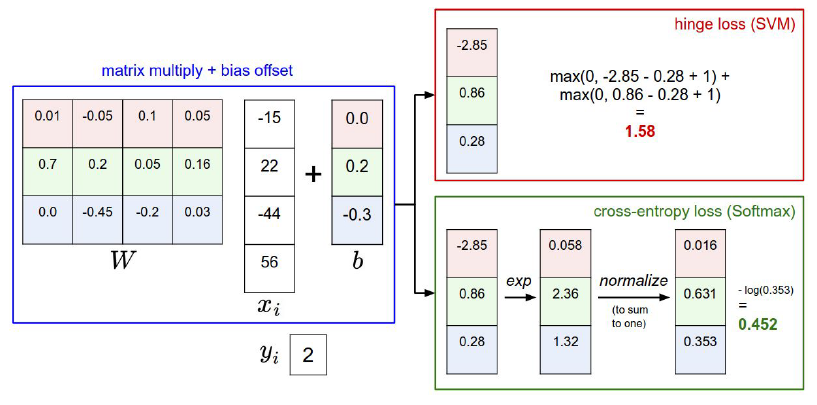
Multiclass SVM loss (两分类的SVM的泛化),使SVM损失计算了所有的不正确的例子,as follows:

where 将所有不正确类别的评分与正确类别的评分之差加1,并将得到的结果与0作比较,取两者中的最大值,然后将所有的数值进行求和。
目的是使得正确类别的评分要高于错误类别,还使用了一个安全系数,系数值为1(安全系数的选择是随意的),例子:

猫的得分为3.2, 理性情况下我们希望其他类别的得分最高为2.2(2.2-3.2+1=0), 但是car 得分高于2.2, 得到的2.9体现了这种不理想程度。
最后再进行一个相对转化,取训练集中所有损失结果的平均值,as follows:

为什么对损失取了平均? 因为这个类的数量是一个常数,意味着在损失函数前加了1/3这个系数,我们的最终结果是将W/loss最小化,所以
你无论将损失减小还是成比例的改变图像的大小,都不会改变结果, 得到最优的W,取平均的方法可以认为是参数变化,取平均和取和都不会影响最后的结果。
如果损失进行缩放(scaling)和平移,我们是在非线性的改变SVM,进行这个选择是比较困难得。

上面的公式成为square hinge loss,这个为hinge loss,不同的计算方法都可以使用,作为超参数的一种。
我们在优化W时,W的初始是非常小的,导致在开始时分数是很接近0的,如果所有的分数都接近0,损失函数是怎样的呢?
得到的结果是类的数量减去1,在开始时你可以检查你的损失函数得到的第一个值,你这个函数基本正确,是非为理论的第一个损失值。

margins[y]=0,因为如果照上式会计算为1,我们将它设置为0,本身正确的相减, 实施了矢量化,
在整个实例中,损失的完整形式。
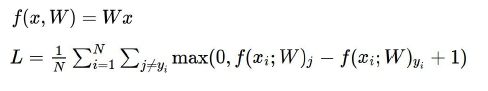
但这个公式,有一些缺点,要使得loss 为0, 那么这个W是否是唯一的呢?
如果改变权值使它越来越大,则分数间的差值就会越来越大,这是一个线性损失,拥有一个最佳的完整的W的子空间,
由损失可知,他们都是完全相同的,这不是一个好的性质,as follows:

W变为原来的两倍,他们得分之间的差值会变大,但是结果却没有变。
如果所有的差值都为负数,增大为两倍后会变得越来越负,所以你得到的值会很小,所以这个取最大值的结果会一直为0.
不管数据集,只考虑W最优的情况,并引入正则化的概念(weight regularization):
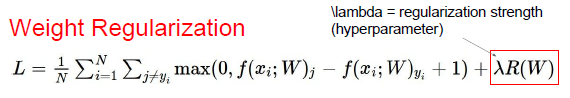
R(W)正则化函数,衡量了W的好坏, 我们不仅仅想要数据拟合得很好,也希望优化W。
正则化是衡量你的训练损失和你用于测试集的泛化损失,是一系列通过损失来使目标相加的技术,它将一直和这个东西形成竞争,
所以这个东西想要适应你的训练数据,而这个想要W呈现一种特殊的方式,所以在目标中他们会相互竞争。
加上正则化技术虽然有时会使你的训练错误变得更多,甚至造成错误的分类,但是,他会使测试结果表现得更好,
正则化函数的常见形式:

L2: 假设W是一个二维矩阵,所以我们将以行和列对每个元素的平方取和,然后将他们加入到损失函数中去,一个特殊的正则化,他希望W为0,如果正则化
函数全部为0 的话他的效果就会非常好,但他不可能全部为0,因为那样你就不能分类了,所以他们将会相互竞争。
L2正则化是最常见的形式
用一个例子说明L2正则化的motive:

分别两个权重,得到的结果都为1,但正则化项的存在使得其中一个W优于另一个,尽管在loss function 他们的表现是一直的。
第二组的权重会更好,因为第二组权重考虑了X输入的大部分东西,可以这么说L2正则化要做的就是尽可能的展开W权重,L1正则化可以实现稀疏(如果使用L1加入到损失函数,
你会发现很多W的值都为0了,)
in order to 考虑所有的输入特征或者所有像素,尽可能多的利用这些维度,如果得到相同的结果比只关注一个维度更好,在实际信息挖掘
和处理通常也是这样的。
在实际应用中SVM和softmanx分类是两种选择,他们普遍用于线性分类器中,通常softmax分类器(softmax classifier =》 )更受欢迎。
不把分数理解为某种边界,而是对应不同类未经标准化的对数概率:

如图得到了这张图像为标准化的对数概率,或者说,我们假设这些分数是未标准化的对数概率,那么得到不同类比如猫类概率的方法就是:
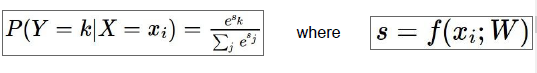
把这些分数作为e的指数从而得到未标准化的概率,然后通过标准化得到标准化的概率,所以除以
这些项的和,得到某张图对应一个类的概率表达式,这个函数就是我们成为的softmax函数,重点在于除以所有分数项的和,如果我们让这些分数表示属于不同类别的概率,就一定要清楚我们想要实现什么,不同类别的概率中有一个是正确的,所以我们想要使正确分类概率的的对数最大:
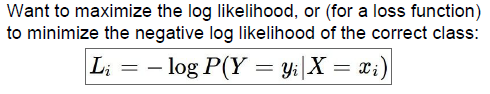
根据损失函数,我们使负的正确分类概率的对数最小,这就是想要的损失函数,
所以正确分类概率的对数要高,那么负的就要很低,所以说概率对数是分数的扩展,所以真正的表达式为:

这就是损失函数,负的那个表达式的对数,例子:

要让概率对数最大化,从mathematics来说最大化概率值并不好,所以通常最大化概率对数
,最小化负的概率对数,0.89就是得到的最终损失函数值,我们在这个softmax中损失就是0.89
损失函数的最大值和最小值是多少?
如果概率为1,则损失为0,概率为0,最大值为无穷,和svm一样
如果初始化W很小,score接近0,那么损失呢?
损失为类数分之一的对数去负数,通常会记录下分类数目,看期望的第一次损失值是多少。
希望正确类得到一个高过错误类的分数。 或者理解成未标准化的对数概率,通过下图所示的框架得到概率值,尽可能增加正确分类的概率。
当你使用逻辑回归时,如果想要最大化概率,那使用log无意义,因为log是单调函数
最大化概率和最大化对数概率等价,但从mathematic出发,将概率变为对数形式更加优美
Softmax和SVM就损失函数的比较

对于SVM来说,对错误分类进行了忽视,具有附加的稳定性,一旦满足边界条件即误分类小于正确分类评分减一,样例点不影响损失函数;而对于Softmax任何一个测试样例都会提升分类器的性能,softmax对于函数每一个样本点都有关注,考虑所有样。
SVM对于接近分类边界的样例较为敏感, 对远离边界的不敏感。
Softmax是一个基于所有数据的函数,对所有样例点都有考虑,对所有数据考虑。
整个损失的求解过程:
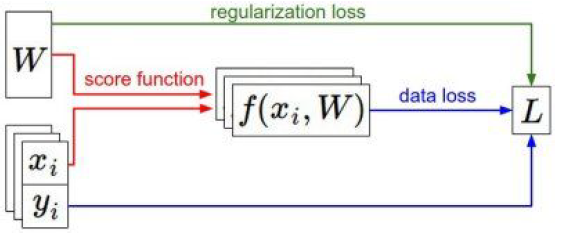
左下角的x和y,分别代表你的图片数据集和标签数据集,正则化只用于权重而不用于数据,只控制W,降低损失。
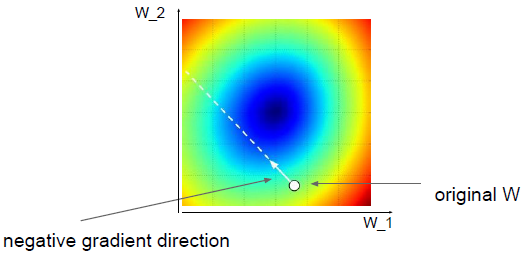
优化: 损失值处在一个高纬度的W空间里,如果的使用random search 你看不到山谷,但是你知道每一点(w)的高度(损失值),你试图到达山谷的最低端。
所以想要到山谷的最低端我们使用梯度(或者说计算每个方向上的斜率),计算斜率,试图向下走。
跟着斜率走:

如图的斜率公式,就是一个求导的过程,而对于多维空间,可以建立导数的向量,分别对应每个维度上的梯度,所以当处理多维空间时,我们有多维的W,所以对应使用多维的梯度,这就是梯度的一个公式。
下面给出一个梯度的求解例子,找出一个方法求解这些点的斜率,通俗点计算我在山谷里像某个方向迈出了一小步,观察我是向上走了还是向下走了,梯度可以告诉我是向上走了还是向下走了。
所以假设走了一小步,损失是1.25,根据公式,使用差值处以h得到梯度值-2.5,因为斜率是负的
向下走的,所以我走了一小步,损失值变小了,所以对应每个维度都可以使用这种方法求解。

对于第二个维度,加上一个小数值h给W,把损失的差值和h的值带入公式,梯度
结果为0.6.

第三个维度进行相同的操作,得到的梯度结果等于0
给出了求解梯度的数值方程:

求解梯度的python代码,遍历所有W:

但是我们需要对每一个维度求解梯度,但是当参数很大时,遍历很蠢,而且要求解到损失才能够得到得到梯度。
求解梯度的过程为:

不需要计算出每个维度的梯度,可以使用微积分,写出梯度的公式,就不用反复求解损失值来找到到底是向上走了还是向下走了,使用微积分求解整个过程。
总结一下,数值梯度计算缓慢数值不准确,但是写起来简单。但是需要不断的重复同样的步骤求解损失方程,再得到梯度。
使用微积分求解梯度,再最后使用数值梯度的方法来检验结果是否正确。
优化时。 整个循环是用来使用损失值求解梯度的,知道梯度后我们可以对参数进行升级。

一点一点的改变W的值,使用负的步长数乘以梯度。 因为要找出损失值的最小值,梯度值为负数
才会不断的向下找最小值,步长是一个较难的超参数(学习率),两个参数需要注意学习率和正则化参数lamda。
一般参数,就是不同方向上的斜率,我们一步一步的向最小值走去,再权重空间中。
权重的空间描述,一个W的初始值,得到一个梯度,然后这个梯度上你开始向前走。步长很大,W的值跳跃会很大,逻辑回归问题的凸函数问题,这就像一个碗,我们试图到达碗底,这个wan
在实际操作中,我们在整个训练过程中都不会去测试这个损失函数的实际值,只是从数据集里面取一个mini-batch,实际操作中只是取出一批进行计算,由于只取了训练集的一部分,所以得到的梯度很可能一个噪声, 这个就是缺点,但是速度快可迭代次数可以达到很大。
mini-batch的表现效率更高,使用所有的数据去算梯度不现实,选择合适的mini-batch匹配GPU
如果使用了非常不正确的初始值则开始的时候会有一个很明显的下降趋势。
不同的学习率在损失函数上影响的效果的图像,

有很多种方法完成参数的更新,SGD, momentum方法(你可以把这个优化过程想象成一个速度的轨迹,进行循环,就是在构建这个速度的轨迹,在我们找到正确的梯度方向后,我们提高在这个方向上的速度)。
计算机视觉图像特征分析方法:
1. 色彩直方图:色彩的统计特征

2. HOG/SIF:使用图片中不同物体之间边缘的方法来做分类,在图中这些边缘会有不同的方向,我们把不同方向上的边缘用直方图做一个总结,统计一下这张图片上不同方向的边缘都有多少,最后通过这个边缘数量的统计来得出图片是什么?

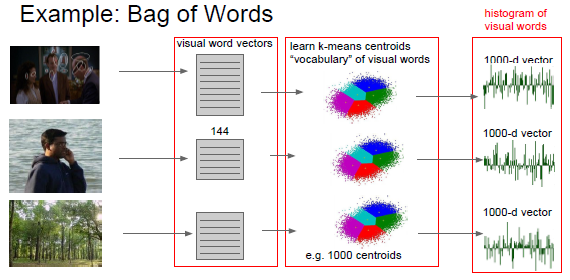
3. 词袋方法(Bag of Words)
首先我们的程序要看到图片上的不同点,然后描述一个个小快上我们看到了什么,比如某个元素的频率、颜色等特征,然后我们使用这些数据形成一个字典,所以我们在图片上看到的东西就是一些蓝色出现的频率有多少的数据,最终得到的结果是一个在图上各种东西出现次数的k均值,举例来说这第三者张图上有很多绿色的东西,所以你看到的是以一个在绿色频率上数值很高的特征向量,然后把计算结果放入线性分类器中:
总结: 在早期的计算机视觉,都是先进行大量的特征工程,再使用线性分类器进行训练:





