Gym 101775 2017-2018 ACM-ICPC Asia East Continent League Final (EC-Final 2017)
传送门
A.Chat Group
不难发现，题目中让我们求的式子为：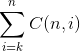
而很显然，因为n相当的大，因此直接做的话绝对会超时，因此考虑将式子转化。
根据组合数的公式，上述的式子可以转化为：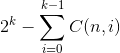
因为此时的k比较小，因此我们利用组合数公式递推求解。
#include <bits/stdc++.h> #define maxn 100005 using namespace std; typedef long long ll; ll inv[maxn+20]; const int mod=1e9+7; void init(){ inv[1]=inv[0]=1; for(int i=2;i<=maxn;i++){ inv[i]=(mod-mod/i)*inv[mod%i]%mod; } } ll powmod(ll a,ll b){ ll res=1; while(b){ if(b&1) res=res*a%mod; b>>=1; a=a*a%mod; } return res; } int main() { init(); int t,n,k,cnt=0; scanf("%d",&t); while (t--){ scanf("%d %d",&n,&k); ll res=1,y=n,sum=1; for (int i=1;i<k;i++){ res=res*y%mod*inv[i]%mod; y--; sum=(res+sum)%mod; } ll ans=(powmod(2,n)-sum+mod)%mod; printf("Case #%d: %lld\n",++cnt,ans); } return 0; }
B.Scapegoat
首先必定是每一口锅都让一个替罪羊去背，因为要使得最后的方差最小，因此我们考虑根据值离总平均值的距离做判断。
因此，我们必定是要让每一口锅平均分配出来的值尽可能的接近总的平均值。为此，我们需要对每一口锅分别记录，Var1=(严重值-平均值)^2 以及 Var2=（加了1个人分锅后的严重值-平均值）^2。而要使得在整体上答案更优，我们必定是首先选取 Var1-Var2比较大的（证明选取它能够使得该锅的值更接近总的平均值）。因此我们只需要用一个优先队列进行维护，每次不断取队顶的锅，将一个人分配到那口锅即可。
#include <bits/stdc++.h> #define maxn 200005 using namespace std; double ave; struct Node{ double all,var1,var2,cur;//Var1和Var2分别代表原来的值离平均值的距离以及(Var1-加上1个人分摊后的值离平均值的距离) int num; bool operator <(const Node &b)const{//在优先队列中维护Var2即可 return var2<b.var2; } Node(double _all,int _num,double _cur){ all=_all,num=_num,cur=_cur; var1=(cur-ave)*(cur-ave)*num; var2=var1-(all/(num+1)-ave)*(all/(num+1)-ave)*(num+1); } }; priority_queue<Node>que; int a[maxn]; int main() { int t; scanf("%d",&t); int Case=0; while(t--){ int n,m,M; scanf("%d%d",&n,&m); M=m; double sum=0; for(int i=0;i<n;i++){ scanf("%d",&a[i]); sum+=a[i]; } ave=sum/m;//计算平均值 for(int i=0;i<n;i++){ Node now=Node(a[i],1,a[i]); que.push(Node(a[i],1,a[i])); } m-=n; while(m--){ Node now=que.top(); que.pop(); que.push(Node(now.all,now.num+1,now.all/(now.num+1))); } double res=0; for(int i=0;i<n;i++){//计算方差 res+=(que.top().cur-ave)*(que.top().cur-ave)*que.top().num; que.pop(); } res/=M; printf("Case #%d: %.8f\n",++Case,res); } }
C.Traffic Light
所有红绿灯的周期都是相同的，而且我们可以调整它的开始状态，我们肯定是要它情况最优，最优的情况就是一直没遇到红灯，所以我们可以这样调整，走到第一个红绿灯时恰好变绿灯，然后接着走，下一个红绿灯调整成也是刚好是变绿灯，所有的灯都这样，这样的情况是最优的，它对应的最差情况就是走到第一个红绿灯的时候不是刚好变绿灯，我们模拟一下就可以知道等红灯的时间最多就是最长的红灯时间。
#include<bits/stdc++.h> using namespace std; const int maxn=1007; int main(){ int t,cnt=0,n; scanf("%d",&t); while (t--){ scanf("%d",&n); double x,y,sum=0,mx=0; for (int i=0;i<=n;i++) { scanf("%lf",&x); sum+=x; } for (int i=1;i<=n;i++){ scanf("%lf%lf",&x,&y); mx=max(y,mx); } sum+=mx; printf("Case #%d: %.8f\n",++cnt,sum); } return 0; }
D.Mr. Panda and Geometric Sequence
首先我们设公比为
，因为要满足一个数列为等比数列，则至少存在三个数，使得他们的公比相同，因此我们可以构造出这三个数分别为：
，
，
。
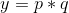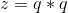因为总的区间的上限为1e15，要满足至少存在三个数，使得他们成等比数列，则x，y，z的值的上限必定为1e5。因此我们可以考虑分别枚举p和q。又因为对于任意的p和q，可能又多个结果符合条件，因此我们仍然需要再枚举一个k，继而分别得到三个数
，
，
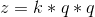。之后我们只需要将这三个数分别转化成原来的数，并将这个数存在一个桶中。
因为可能存在三个以上的数的等比数列，因此我们只需要对最后一个z不断乘上公比，并判断是否能够被p整除即可。
最后将桶里存的数进行排序并去重，对于每一个询问[l,r]只需要在桶里二分找到第一个大于r，以及第一个大于l-1的坐标，两式相减即为答案。
#include <bits/stdc++.h> using namespace std; typedef long long ll; vector<ll>vec; ll Pow[20]; int Count(ll n){//获取位数 int cnt=0; while(n){ n/=10; cnt++; } return cnt; } void init(){ int n=1e5; Pow[0]=1; for(int i=1;i<=16;i++) Pow[i]=Pow[i-1]*10; for(int p=1;p<=n;p++){ for(int q=p+1;q<=n/p;q++){//分别枚举p和q if(__gcd(p,q)>1) continue;//如果p和q不互质，则跳过判断 for(int k=1;k<=n/p/q;k++){ ll x=1ll*k*p*p,y=1ll*k*p*q,z=1ll*k*q*q;//构造三个数 ll numx=Count(x),numy=Count(y),numz=Count(z);//分别获取三个数的位数 ll numall=numx+numy+numz; if(numall>15) break;//如果总位数>15直接跳出 ll now=z,res=x*Pow[numy+numz]+y*Pow[numz]+z;//将原来的数还原，并存到桶里 vec.push_back(res); while(1){ if(now%p!=0) break;//如果之后的数不能被p整除，则跳出 //否则继续统计答案 now=now*q/p; if(numall+Count(now)>15) break; numall+=Count(now); res=res*Pow[Count(now)]+now; vec.push_back(res); } } } } //排序并去重 sort(vec.begin(),vec.end()); vec.resize(unique(vec.begin(),vec.end())-vec.begin()); } ll Sum(ll n){//二分求下标 return upper_bound(vec.begin(),vec.end(),n)-vec.begin(); } int main() { int t; init(); scanf("%d",&t); int Case=0; while(t--){ ll l,r; scanf("%lld%lld",&l,&r); printf("Case #%d: %lld\n",++Case,Sum(r)-Sum(l-1)); } return 0; }
E.Snakebird
F.Good Number
G.Image Recognition
H.Mr. Panda and Birthday Song
首先说一下题意：
给你一个长度不大于1e6的字符串（由，'a'-'z'或‘？’组成，且‘？’可转化为任意小写字母），以及两个数x，y。
现在有两个条件：
1）字符串中存在任意一个长度为x的子串均为元音，或存在任意一个长度为y的子串均为子串。
2）字符串中存在任意一个长度为x的子串不都是元音，且存在任意一个长度为y的子串不都是辅音。
如果同时满足条件（1）（2），则输出SURPRISE；如果只满足（1），则输出（DISLIKE）；如果只满足（2），则输出（LIKE）。
首先，对于方案（1），我们遍历一遍整个字符串，在‘？’的条件下，默认将元音和辅音的连续数都+1，并记录最大值判断即可。
因此，我们只需要考虑如何处理出第二种情况。首先我们可以判断，因为要求任意一个连续的元音/辅音小于x/y，因此我们考虑要使得他们连续的尽可能小。
因此我们考虑用dp对此进行维护。我们设dp[i][0/1]，（0代表元音，1代表辅音）为位于第i号的结点时最小的连续的元音/辅音的个数。
对于某个位置的字符倘若为元音，倘若之前的状态为连续元音，则此需要将连续元音的数量+1；而倘若之前的状态为连续辅音，则此时需要将连续元音的数量重新置为1。
对于某个位置的字符为辅音的情况同理。
而对于某个位置为‘？’的情况如果之前的状态为连续的元音，则此时可以将辅音清零；如果之前的状态为连续的辅音，则此时可以将元音清零。之后只需要不断维护他们的最小值即可。倘若发现在某一个状态下，连续元音数超过x，连续辅音数超过y，则证明不满足条件（2）。
#include <bits/stdc++.h> #define maxn 1000005 using namespace std; int dp[maxn][2]; char str[maxn]; int x,y; bool judge(char c){ if(c=='a'||c=='e'||c=='i'||c=='o'||c=='u') return 1; else return 0; } int main() { int t; int Case=0; scanf("%d",&t); while(t--){ scanf("%s",str); scanf("%d%d",&x,&y); int len=strlen(str); int vow=0,cons=0; int maxv=0,maxc=0; for(int i=0;i<len;i++){ if(str[i]=='?'){ vow++,cons++; maxv=max(maxv,vow); maxc=max(maxc,cons); continue; } if(judge(str[i])){ vow++; maxv=max(vow,maxv); cons=0; } else{ cons++; maxc=max(maxc,cons); vow=0; } } int flag1=0,flag2=1; if(maxv>=x||maxc>=y) flag1=1; memset(dp,0x3f3f3f3f,sizeof(dp)); dp[0][1]=dp[0][0]=0; for(int i=1;i<=len;i++){ if(str[i-1]=='?'){ if(dp[i-1][0]<x) { dp[i][0]=dp[i-1][0]+1; dp[i][1]=1; } if(dp[i-1][1]<y){ dp[i][1]=min(dp[i][1],dp[i-1][1]+1); dp[i][0]=1; } } else if(judge(str[i-1])){ if(dp[i-1][0]<x) dp[i][0]=dp[i-1][0]+1; if(dp[i-1][1]<y) dp[i][0]=1; } else{ if(dp[i-1][1]<y) dp[i][1]=dp[i-1][1]+1; if(dp[i-1][0]<x) dp[i][1]=1; } if(dp[i][0]>=x&&dp[i][1]>=y){ flag2=0; break; } } printf("Case #%d: ",++Case); if(flag1&&flag2) puts("SURPRISE"); else if(flag1) puts("DISLIKE"); else if(flag2) puts("LIKE"); } return 0; }
I.PLAYERUNKNOWN'S BATTLEGROUNDS
J.Straight Master
可以发现3，4，5可以凑出任意的3以上的数，还可以发现这个数列一直到第（n+1）位必然是升降相对应的，所以直接维护一个差分，相隔三以上的就可以正的负的相互怼掉，判断最后所剩的是否是0就可以了
#include<bits/stdc++.h> using namespace std; const int maxn=2e5+5; int T,n; int a[maxn],b[maxn]; void read(int &ret){ ret=0; char ch=getchar(); while(ch>'9'||ch<'0') ch=getchar(); while(ch>='0'&&ch<='9'){ ret=ret*10+ch-'0'; ch=getchar(); } } int cas; int main(){ read(T); while(T--){ read(n); for(int i=1;i<=n;i++) {read(a[i]);b[i]=a[i]-a[i-1];} b[n+1]=-a[n]; bool flag=0; if(b[2]<0||b[3]<0){printf("Case #%d: No\n",++cas);continue;} long long sum=0; for(int i=1;i<=n+1;i++){ if(b[i]>0) sum+=b[i]; int nxt=i+3; if(nxt>n+1) break; else if(b[nxt]<0) sum+=b[nxt]; if(sum<0){flag=1;break;} } if(flag||sum) printf("Case #%d: No\n",++cas); else printf("Case #%d: Yes\n",++cas); } return 0; }
K.Downgrade
温暖的签到题，根据题意模拟一下即可
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int maxn=100005; int val[maxn]; long long sum[maxn]; int main(){ int T,cas=0; scanf("%d",&T); while(T--){ ll A,B,n; scanf("%lld%lld%lld",&A,&B,&n); for(int i=1;i<=A;i++){scanf("%d",&val[i]);sum[i]=sum[i-1]+val[i];} int m=A; while((n--)){ int tmp1,tmp2; tmp1=lower_bound(sum+1,sum+m+1,A)-sum; tmp2=A-sum[tmp1-1]; if(tmp1==A) { B=tmp2; break; } A=tmp1,B=tmp2; } printf("Case #%d: %lld-%lld\n",++cas,A,B); } return 0; }
L.SOS
想要获胜，就要构造出S S这种情况
n为奇数时，后手构造出来是赢不了的
n为偶数时，先手构造出来是赢不了的
当n<=6时双方都无法构造出来
当n>=7时，先手可以构造出来，必胜
当n>=16时，后手可以构造出来，必胜
其他情况为平局，双方都无法必胜
#include <bits/stdc++.h> #define maxn 100005 using namespace std; int main() { int T,n; scanf("%d",&T); for(int cas=1;cas<=T;cas++){ scanf("%d",&n); if(n<=6)printf("Case #%d: Draw\n",cas); else if((n&1))printf("Case #%d: Panda\n",cas); else if (n>=16) printf("Case #%d: Sheep\n",cas); else printf("Case #%d: Draw\n",cas); } return 0; }
M.World Cup
温暖的签到题，只需要知道小组赛时有48场比赛，16强有8场比赛，8强有4场比赛，半决赛有2场比赛，决赛有1场比赛即可。
最后模拟一下就OK了。
#include<bits/stdc++.h> using namespace std; int di[5]={1,49,57,61,63}; int val[5]; int main(){ int T; long long ans; scanf("%d",&T); int cas=0; while(T--){ for(int i=0;i<5;i++) scanf("%d",&val[i]); ans=0; int n; scanf("%d",&n); for(int i=1;i<=n;i++){ int id; scanf("%d",&id); for(int j=4;j>=0;j--){ if(id>=di[j]){ ans+=val[j]; break; } } } ans*=10000; printf("Case #%d: %lld\n",++cas,ans); } return 0; }
