HDU 2256(矩阵快速幂)
题面:
Total Submission(s): 1681 Accepted Submission(s): 1036
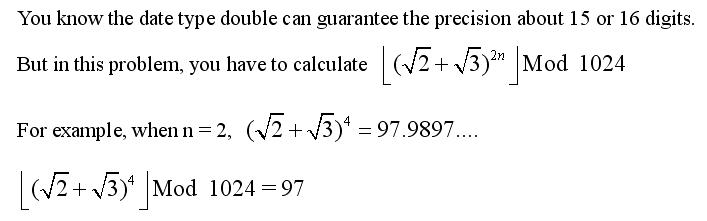
Problem of Precision
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 1681 Accepted Submission(s): 1036
Problem Description
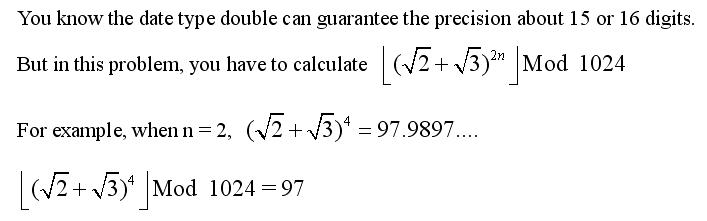
Input
The first line of input gives the number of cases, T. T test cases follow, each on a separate line. Each test case contains one positive integer n. (1 <= n <= 10^9)
Output
For each input case, you should output the answer in one line.
Sample Input
3
1
2
5
Sample Output
9
97
841
Source
题面分析:题面要我们求的就是一个多项式的值,看到n的数据范围1e9,因此直接递推过去求解肯定不可行,因此得考虑使用矩阵快速幂加速求解。但是这道题的难点就是当你化简出式子之后,还得考虑通过近似化使最后答案中的根号去除(反正我是先不到的了━┳━ ━┳━),附上推导式:

最后一步的近似化真的太骚了(不看题解真的想不出来/(ㄒoㄒ)/~~)受教受教!!
之后就是简单的矩阵快速幂的模板即可。
#include <bits/stdc++.h>
using namespace std;
const int mod=1024;
struct martix{
int mo[3][3];
martix(){
memset(mo,0,sizeof(mo));
}
};
martix q;
martix mul(martix a,martix b){
martix c;
for(int i=0;i<2;i++){
for(int j=0;j<2;j++){
for(int k=0;k<2;k++){
c.mo[i][j]=(c.mo[i][j]+a.mo[i][k]*b.mo[k][j])%mod;
}
}
}
return c;
}
martix powmo(martix a,int n){
martix T;
for(int i=0;i<2;i++){
T.mo[i][i]=1;
}
while(n){
if(n&1) T=mul(a,T);
n>>=1;
a=mul(a,a);
}
return T;
}
int main()
{
int t;
cin>>t;
q.mo[0][0]=5,q.mo[0][1]=12,q.mo[1][0]=2,q.mo[1][1]=5;
while(t--){
int n;
cin>>n;
martix res=powmo(q,n);
cout<<(2*res.mo[0][0]-1)%mod<<endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号