Codeforces 985D（二分答案）

传送门

题面：

 

D. Sand Fortress

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are going to the beach with the idea to build the greatest sand castle ever in your head! The beach is not as three-dimensional as you could have imagined, it can be decribed as a line of spots to pile up sand pillars. Spots are numbered 1 through infinity from left to right.

Obviously, there is not enough sand on the beach, so you brought n packs of sand with you. Let height hi of the sand pillar on some spot ibe the number of sand packs you spent on it. You can't split a sand pack to multiple pillars, all the sand from it should go to a single one. There is a fence of height equal to the height of pillar with H sand packs to the left of the first spot and you should prevent sand from going over it.

Finally you ended up with the following conditions to building the castle:

• h1 ≤ H: no sand from the leftmost spot should go over the fence;
• For any 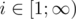 |hi - hi + 1| ≤ 1: large difference in heights of two neighboring pillars can lead sand to fall down from the higher one to the lower, you really don't want this to happen;
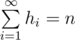• : you want to spend all the sand you brought with you.

As you have infinite spots to build, it is always possible to come up with some valid castle structure. Though you want the castle to be as compact as possible.

Your task is to calculate the minimum number of spots you can occupy so that all the aforementioned conditions hold.

Input

The only line contains two integer numbers n and H (1 ≤ n, H ≤ 1018) — the number of sand packs you have and the height of the fence, respectively.

Output

Print the minimum number of spots you can occupy so the all the castle building conditions hold.

Examples

input

Copy

5 2

output

Copy

3

input

Copy

6 8

output

Copy

3

Note

Here are the heights of some valid castles:

• n = 5, H = 2, [2, 2, 1, 0, ...], [2, 1, 1, 1, 0, ...], [1, 0, 1, 2, 1, 0, ...]
• n = 6, H = 8, [3, 2, 1, 0, ...], [2, 2, 1, 1, 0, ...], [0, 1, 0, 1, 2, 1, 1, 0...] (this one has 5 spots occupied)

The first list for both cases is the optimal answer, 3 spots are occupied in them.

And here are some invalid ones:

• n = 5, H = 2, [3, 2, 0, ...], [2, 3, 0, ...], [1, 0, 2, 2, ...]
• n = 6, H = 8, [2, 2, 2, 0, ...], [6, 0, ...], [1, 4, 1, 0...], [2, 2, 1, 0, ...]

 

题目描述：

    你有n堆沙子，最左边的沙子的最大高度不能超过H，让你在一个从1到正无穷的一维平面内放沙子，且要满足相邻两个坐标的沙子的高度不能超过1。问沙子能够占用的最少坐标点的个数。

题目分析:

    这个题实质上有一个隐藏条件，因为题目要求相邻两个坐标的沙子高度不能超过1，这代表最后一堆沙子的个数也必定为1。而题目要我们求占用坐标点的最少个数，根据贪心的思想，要使占用的点最少，则我们必须要贪心地令沙子的高度尽可能高。然而又因为最后一堆的沙子的个数为1，因此我们可以判断出，沙子的高度所形成的曲线必定是先增后减的或者一直减小的曲线。即——沙子的高度存在单调性！因此我们就可以通过二分答案的方法，不断二分占用坐标的个数即可。

    而二分的check函数，我们因为最优的情况下，两两沙堆相差均为1，因此我们可以运用等差数列求和公式求出总的沙子堆数，并用它与n进行对比今儿二分即可。

    值得一提的是，当枚举出n为奇数的时候，会出现有两个坐标的值均相当的情况，需要格外留意！

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,h;
const ll cnt=2000000000;
bool check(ll x){
    if(x<=h){
        if(x>=cnt) return true;
        return x*(x+1)/2>=n;
    }
    ll a=(x-h)/2+h;
    if(a>=cnt) return true;
    if((x-h)%2!=0)
    return a*(a+1)/2+(a+h)*(a+1-h)/2>=n;
    return a*(a+1)/2+(a-1+h)*(a-h)/2>=n;
}
int main()
{
    cin>>n>>h;
    ll ln=1,rn=n;
    while(ln<=rn){
        ll mid=(ln+rn)>>1ll;
        if(check(mid)) rn=mid-1;
        else ln=mid+1;
    }
    cout<<rn+1<<endl;
}