Codeforces 1041D（双指针）

传送门

题面：

D. Glider

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

A plane is flying at a constant height of hh meters above the ground surface. Let's consider that it is flying from the point (−109,h)(−109,h) to the point (109,h)(109,h) parallel with OxOx axis.

A glider is inside the plane, ready to start his flight at any moment (for the sake of simplicity let's consider that he may start only when the plane's coordinates are integers). After jumping from the plane, he will fly in the same direction as the plane, parallel to OxOx axis, covering a unit of distance every second. Naturally, he will also descend; thus his second coordinate will decrease by one unit every second.

There are ascending air flows on certain segments, each such segment is characterized by two numbers x1x1 and x2x2 (x1<x2x1<x2) representing its endpoints. No two segments share any common points. When the glider is inside one of such segments, he doesn't descend, so his second coordinate stays the same each second. The glider still flies along OxOx axis, covering one unit of distance every second.

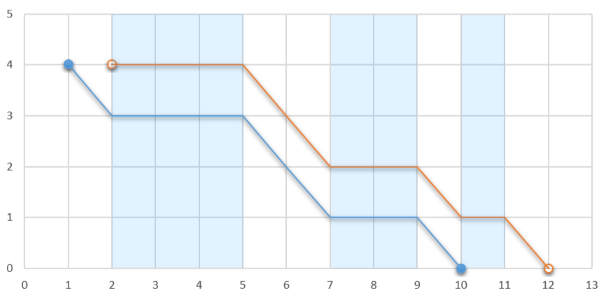If the glider jumps out at 11, he will stop at 1010. Otherwise, if he jumps out at 22, he will stop at 1212.

Determine the maximum distance along OxOx axis from the point where the glider's flight starts to the point where his flight ends if the glider can choose any integer coordinate to jump from the plane and start his flight. After touching the ground the glider stops altogether, so he cannot glide through an ascending airflow segment if his second coordinate is 00.

Input

The first line contains two integers nn and hh (1≤n≤2⋅105,1≤h≤109)(1≤n≤2⋅105,1≤h≤109) — the number of ascending air flow segments and the altitude at which the plane is flying, respectively.

Each of the next nn lines contains two integers xi1xi1 and xi2xi2 (1≤xi1<xi2≤109)(1≤xi1<xi2≤109) — the endpoints of the ii-th ascending air flow segment. No two segments intersect, and they are given in ascending order.

Output

Print one integer — the maximum distance along OxOx axis that the glider can fly from the point where he jumps off the plane to the point where he lands if he can start his flight at any integer coordinate.

Examples

input

Copy

3 4
2 5
7 9
10 11

output

Copy

10

input

Copy

5 10
5 7
11 12
16 20
25 26
30 33

output

Copy

18

input

Copy

1 1000000000
1 1000000000

output

Copy

1999999999

Note

In the first example if the glider can jump out at (2,4)(2,4), then the landing point is (12,0)(12,0), so the distance is 12−2=1012−2=10.

In the second example the glider can fly from (16,10)(16,10) to (34,0)(34,0), and the distance is 34−16=1834−16=18.

In the third example the glider can fly from (−100,1000000000)(−100,1000000000) to (1999999899,0)(1999999899,0), so the distance is 1999999899−(−100)=19999999991999999899−(−100)=1999999999.

题意：

    你现在处于高度为h的地方，每秒y坐标会减少1，x坐标会增加1，而现在会有n个气流区[l,r]，在每个气流区中，你的y坐标不会改变，你的x坐标每秒会增加1。（保证所给出的气流两两之间没有交集）现在你可以从x轴上的任意一点下落，现在问你最远的飞行路径。

题目分析：

    因为题目中保证了气流区两两不相交，因此我们就可以省下来很多讨论的功夫。

    因此，此时只会存在（1）冲过某个气流区后直接落地，（2）冲过某个气流区后，又经过另一个气流区，两种情况。

    因此我们可以采用双指针，分别记录终点和起点的位置，并不断的对上述两种情况讨论，最后枚举所有的气流，记录一下最大值即可。

代码：

#include <bits/stdc++.h>
#define maxn 200005
using namespace std;
struct Node{
    int l,r;
}q[maxn];
typedef long long ll;
int main()
{
    ll n,h;
    cin>>n>>h;
    for(int i=0;i<n;i++){
        scanf("%I64d%I64d",&q[i].l,&q[i].r);
    }
    ll l,r,tmp1,tmp2;
    l=q[0].l,r=q[0].r+h;//首先l指针先指向第一个气流的起点，r指针指向落点
    ll ans=h;
    tmp1=tmp2=0;
    while(tmp1<n){//枚举每一个气流
        while(tmp2+1<n&&q[tmp2+1].l<r){
        //如果下一个气流的左区间在终点前，则证明出现情况2，则将终点加上该气流的区间大小
            tmp2++;
            r+=q[tmp2].r-q[tmp2].l;
        }
        ans=max(ans,r-l);//记录r-l的最大值
        tmp1++;
        l=q[tmp1].l;//将起点置为下一个气流的起点
        r+=q[tmp1].l-q[tmp1-1].r;   //加上气流与气流之间的大小
    }
    cout<<ans<<endl;
}