Gym 101775 D （思维）

传送门：

题面：

D. Mr. Panda and Geometric Sequence

time limit per test

3.0 s

memory limit per test

256 MB

input

standard input

output

standard output

Mr. Panda likes playing with numbers. One day he picked up a number 3612 and found it's interesting. 3612 can be divided into 3numbers 3, 6 and 12 which forms an integer geometric sequence.

An integer geometric sequence is a sequence of at least 3 positive integer numbers a0, a1, ..., an - 1, also there is a positive number D(D > 1) that for each i(0 ≤ i < n - 1), ai × D = ai + 1.

Mr. Panda named this kind of numbers "Happy Number". He also announced that leading zeros are forbidden, which means there should be no extra zeros before the numbers. Now Mr. Panda would like to know how many Happy Numbers are between L and R inclusive.

Input

The first line of the input gives the number of test cases, T. T test cases follow. Each test case contains one line which consists of two numbers L and R.

• 1 ≤ T ≤ 2 × 105.
• 0 ≤ L ≤ R ≤ 1015.

Output

For each test case, output one line containing "Case #x: y", where x is the test case number (starting from 1) and y is the number of Happy Numbers between L and R inclusive.

Example

input

Copy

4
123 124
468 470
248 248
124816 124832

output

Copy

Case #1: 1
Case #2: 1
Case #3: 1
Case #4: 1

Note

In the first test case, the only Happy Number between 123 and 124 is 124, in which 1 × 2 = 2 and 2 × 2 = 4.

In the second test case, the only Happy Number is 248.

In the third test case, the only Happy Number is 469, the common radio is .

In the fourth test case, the only Happy number between 124816 and 124832 is 124816, in which 1 × 2 = 2, 2 × 2 = 4, 4 × 2 = 8 and 8 × 2 = 16.

题意：

    好数的定义为，你可以将这个数分为若干个部分，使得每一个部分可以构成一个等比数列。

    现在给你若干个询问，问你在区间[L,R]中，好数的数量

题目分析：

    首先我们设公比为，因为要满足一个数列为等比数列，则至少存在三个数，使得他们的公比相同，因此我们可以构造出这三个数分别为：，，。

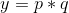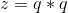    因为总的区间的上限为1e15，要满足至少存在三个数，使得他们成等比数列，则x，y，z的值的上限必定为1e5。因此我们可以考虑分别枚举p和q。又因为对于任意的p和q，可能又多个结果符合条件，因此我们仍然需要再枚举一个k，继而分别得到三个数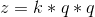，，。之后我们只需要将这三个数分别转化成原来的数，并将这个数存在一个桶中。

    因为可能存在三个以上的数的等比数列，因此我们只需要对最后一个z不断乘上公比，并判断是否能够被p整除即可。

    最后将桶里存的数进行排序并去重，对于每一个询问[l,r]只需要在桶里二分找到第一个大于r，以及第一个大于l-1的坐标，两式相减即为答案。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
vector<ll>vec;
ll Pow[20];
int Count(ll n){//获取位数
    int cnt=0;
    while(n){
        n/=10;
        cnt++;
    }
    return cnt;
}
void init(){
    int n=1e5;
    Pow[0]=1;
    for(int i=1;i<=16;i++) Pow[i]=Pow[i-1]*10;
    for(int p=1;p<=n;p++){
        for(int q=p+1;q<=n/p;q++){//分别枚举p和q
            if(__gcd(p,q)>1) continue;//如果p和q不互质，则跳过判断
            for(int k=1;k<=n/p/q;k++){
                ll x=1ll*k*p*p,y=1ll*k*p*q,z=1ll*k*q*q;//构造三个数
                ll numx=Count(x),numy=Count(y),numz=Count(z);//分别获取三个数的位数
                ll numall=numx+numy+numz;
                if(numall>15) break;//如果总位数>15直接跳出
                ll now=z,res=x*Pow[numy+numz]+y*Pow[numz]+z;//将原来的数还原，并存到桶里
                vec.push_back(res);
                while(1){
                    if(now%p!=0) break;//如果之后的数不能被p整除，则跳出
                    //否则继续统计答案
                    now=now*q/p;
                    if(numall+Count(now)>15) break;
                    numall+=Count(now);
                    res=res*Pow[Count(now)]+now;
                    vec.push_back(res);
                }
            }
        }
    }
    //排序并去重
    sort(vec.begin(),vec.end());
    vec.resize(unique(vec.begin(),vec.end())-vec.begin());
}
ll Sum(ll n){//二分求下标
    return upper_bound(vec.begin(),vec.end(),n)-vec.begin();
}
int main()
{
    int t;
    init();
    scanf("%d",&t);
    int Case=0;
    while(t--){
        ll l,r;
        scanf("%lld%lld",&l,&r);
        printf("Case #%d: %lld\n",++Case,Sum(r)-Sum(l-1));
    }
    return 0;
}