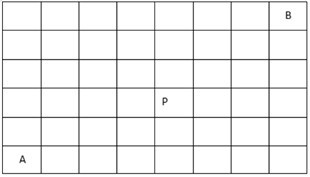
【组合数学+动态规划】在如下8*6的矩阵中，请计算从A移动到B一共有____种走法。要求每次只能向上或向右移动一格，并且不能经过P。

在如下8*6的矩阵中，请计算从A移动到B一共有__种走法。要求每次只能向上或向右移动一格，并且不能经过P。 

A:456 
B:492 
C:568 
D:626 
E:680 
F:702

解析: 
8*6的矩阵，从左下角A到右上角B，一共需要走12步，其中5步向上，7步向右，因此总的走法一共有C(12,5)=792种，但题目规定不能经过P，因此需要减去经过P点的走法。 
经过P的路径分为两部分，从A到P，从P到B。 
同理，从A到P的走法：C(6,2)=15； 
同理，从P到B的走法：C(6,3)=20； 
因此从A到B经过P点的走法有15*20=300种， 
所以从A到B不经过P点的走法有792-300=492种。

这题其实可以用程序算出来 
简单的动态规划 
dp[i][j] = dp[i][j-1] + dp[i-1][j];

代码如下:

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <algorithm>
 4 #include <string>
 5 
 6 using namespace std;
 7 int main()
 8 {
 9 
10   int dp[100][100] = {0};
11 
12   for(int i = 1; i <= 6; i++)
13     for(int j = 1; j <= 8; j++)      
14         dp[i][j] = dp[i-1][j] + dp[i][j-1];
15     
16     int dp2[100][100] = {0};
17     dp2[0][1] = 1;
18 
19     for(int i = 1; i <= 4; i++)
20         for(int j = 1; j <= 4; j++)
21             dp2[i][j] = dp2[i-1][j] + dp2[i][j-1];
22 
23     cout<<dp[6][8] - dp2[4][4] * dp[3][5]<<endl;
24 
25   return 0;
26 }

 或者如下图：

posted @ 2016-03-03 15:22  ZH奶酪  阅读(5290)  评论(0)  编辑  收藏  举报