【2020春】李宏毅机器学习（Classification/高斯分布/逻辑回归vs线性回归）

https://www.bilibili.com/video/av94519857?p=10
https://www.bilibili.com/video/av94519857?p=11

表格最左一列和最上一行

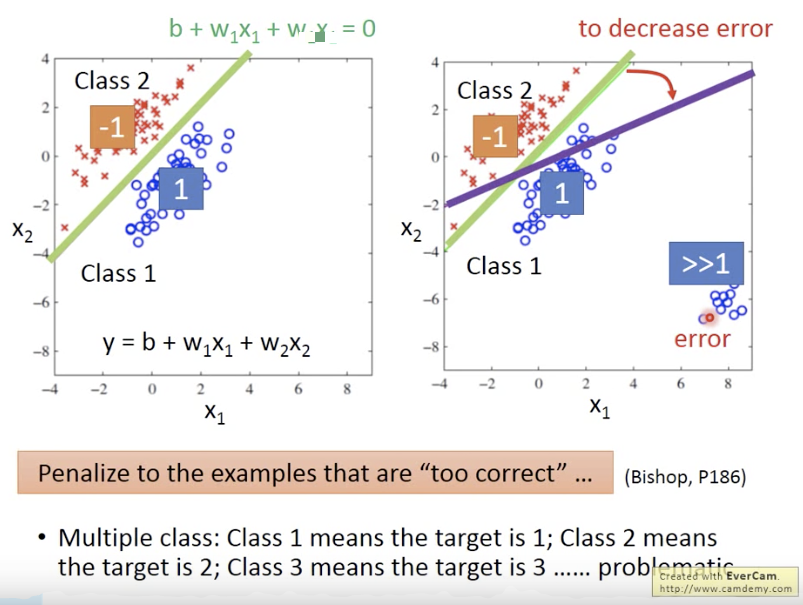
如果用regression的方法去做classification，就会发生右图的情况。

生成式模型

先验概率

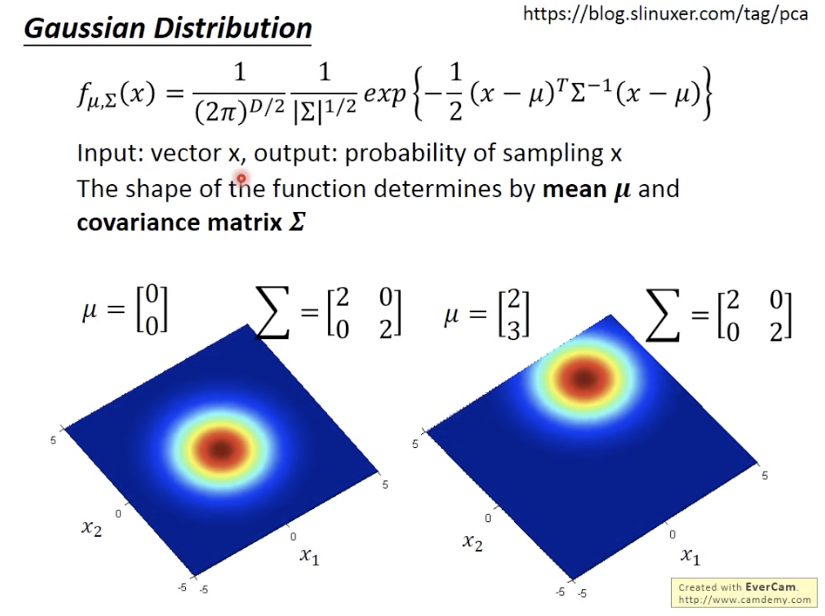
高斯分布

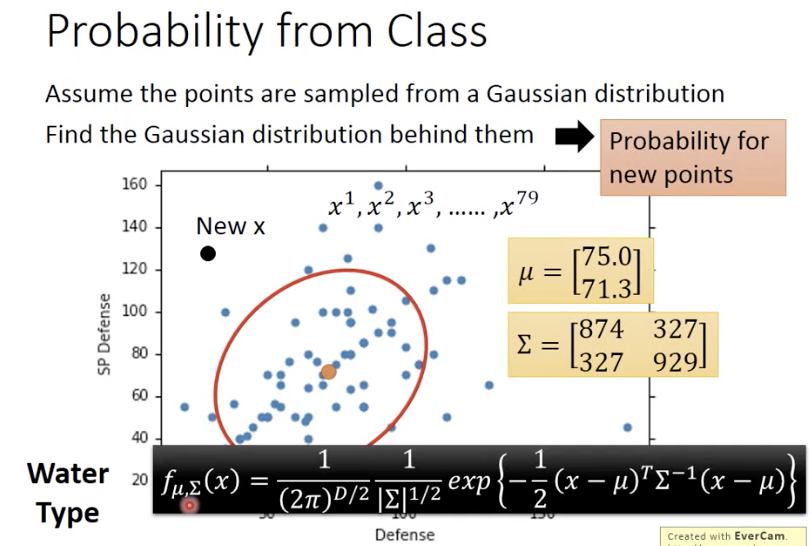
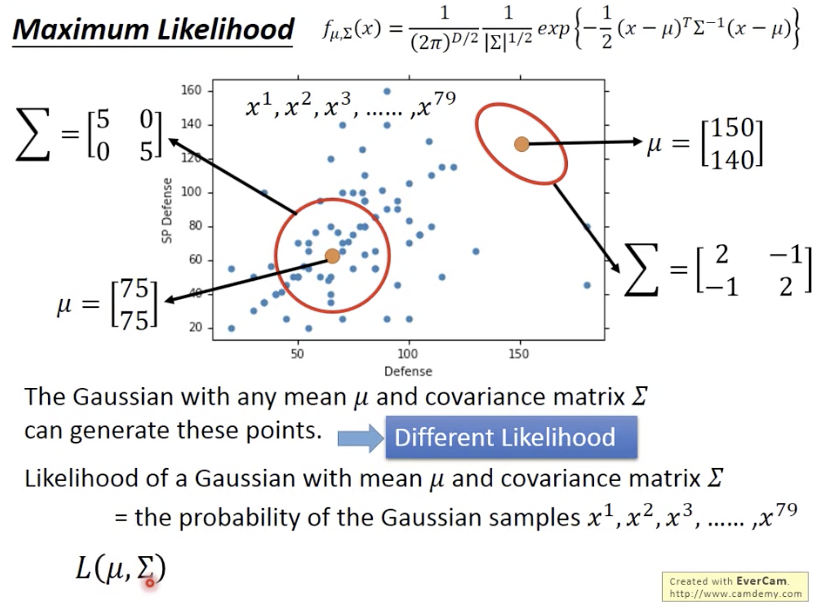
通过极大似然，找到高斯分布

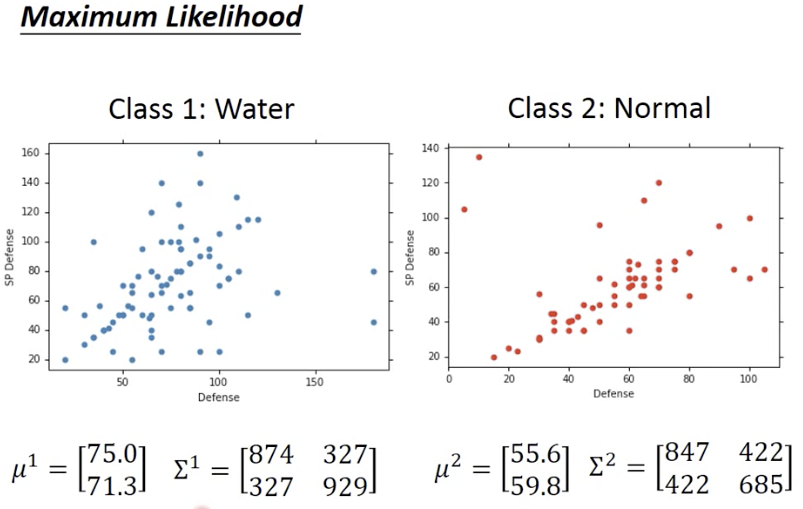
然后通过高斯分布，计算类别：

2个特征得到47% acc，7个特征得到54% acc

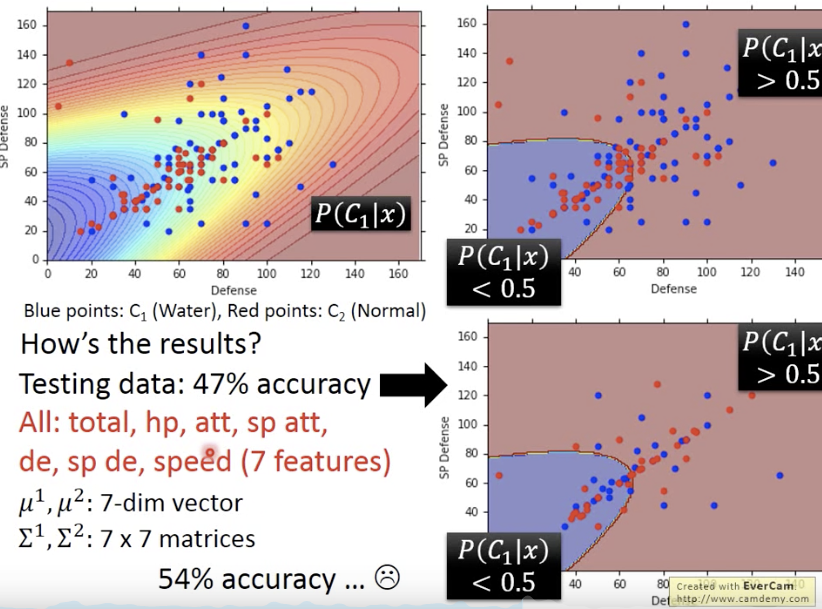
减少模型复杂度，降低过拟合

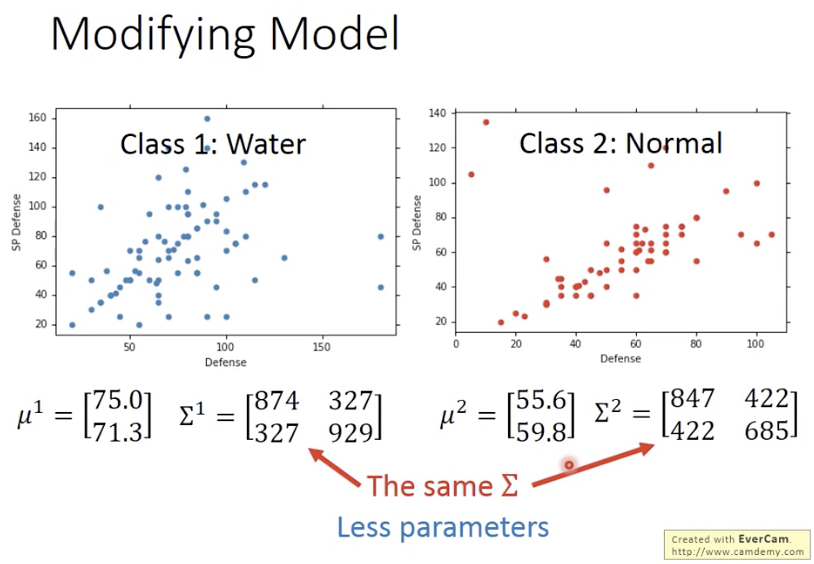
共用同个covariance matrix，线性边界

可以选任何概率分布 / 特征独立就是朴素贝叶斯分类

后验概率

sigmoid等价高斯分布

逻辑回归

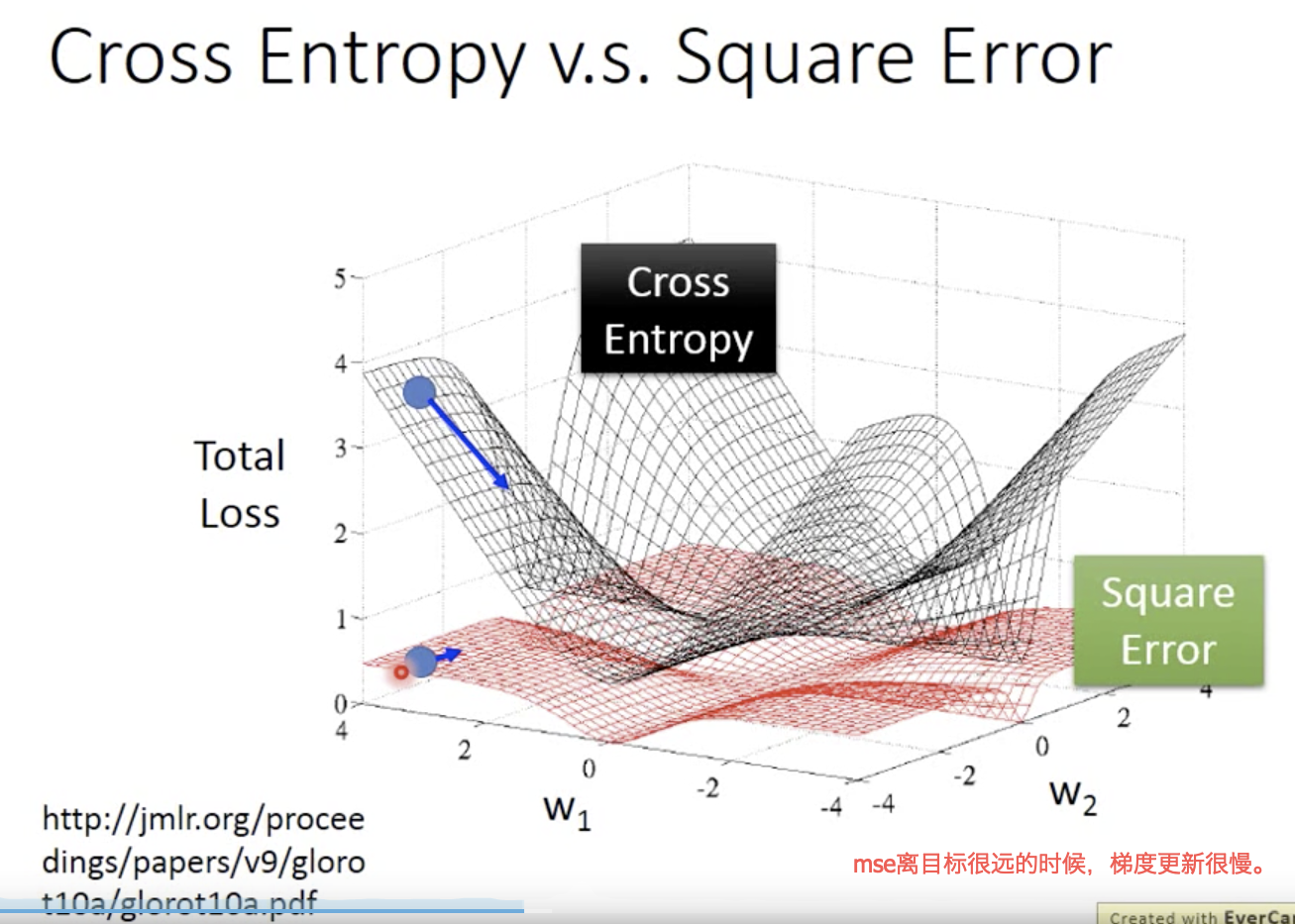
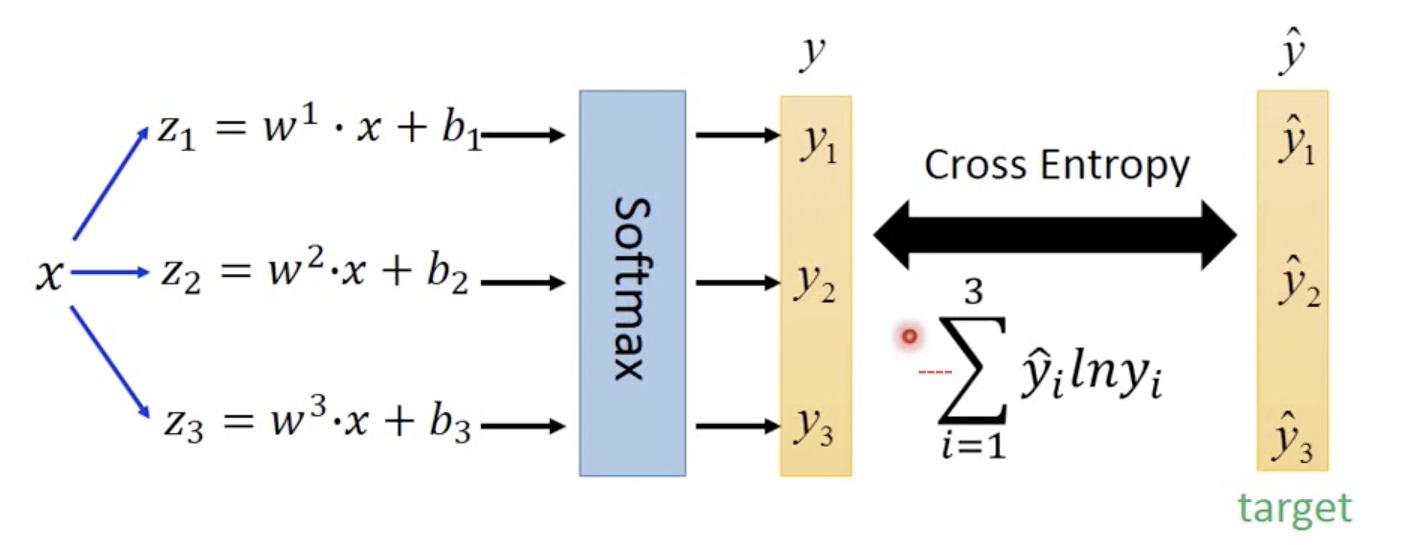
二分类交叉熵损失函数

两个伯努利分布的交叉熵（一个是ground truth，一个是prediction）

逻辑回归和线性回归对比

逻辑斯蒂回归和线性回归的梯度更新公式一样，区别是：

• y_hat的值，一个是0/1，一个是real number；
• output的值，一个是0到1之间，一个是real number；
  

为什么逻辑斯蒂回归不能和square error？【梯度更新公式不是一样吗？？？？这里没搞明白。】

如果y_hat是1，那么当y_pred=1时，梯度接近0，当y_pred=0是，梯度还是接近0；

如果y_hat是0，也同样情况：

判别式模型/生成式模型

逻辑斯蒂回归是判别式模型；

通过高斯分布拟合模型是生成式模型（做了较多假设/分布等）；

下图问题答案：不是同样的w和b

通常判别式模型比生成式模型表现好：

在人类看来很简单的问题，但是生成式模型朴素贝叶斯可能处理不好：

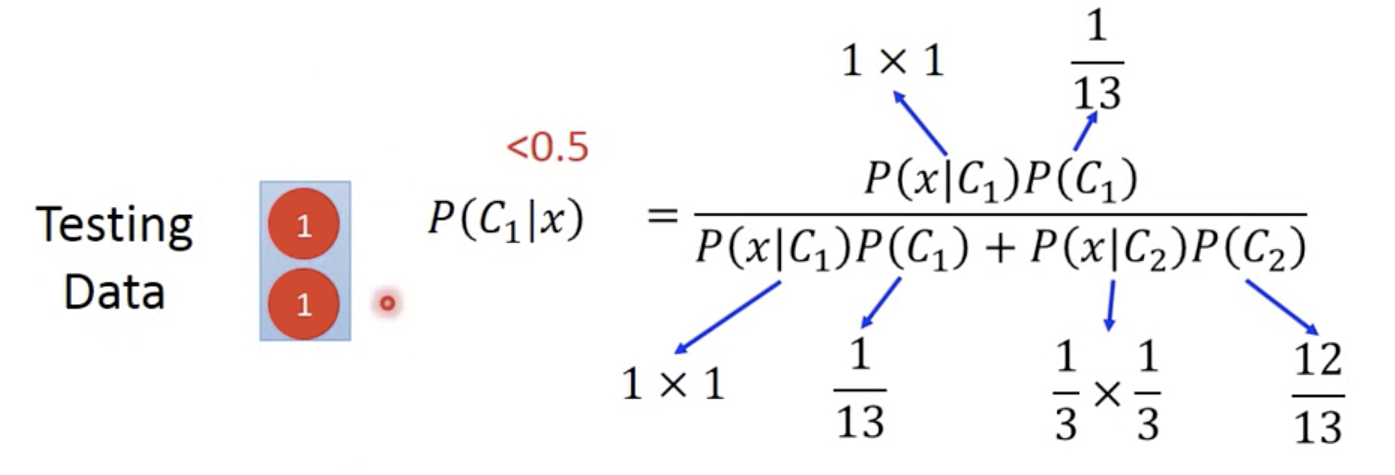
生成式模型的优势：（第三点，例如语音识别）

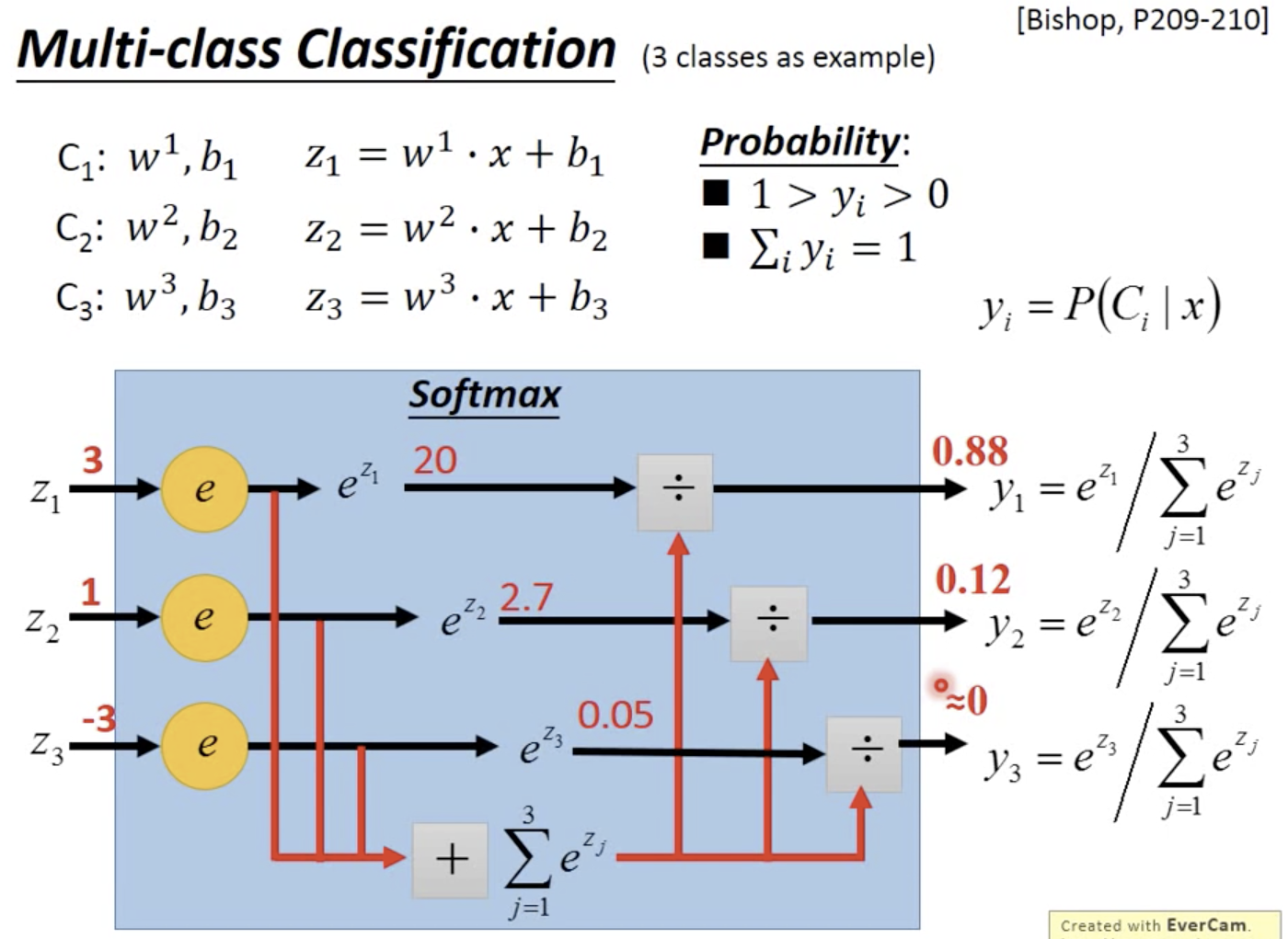
多分类

softmax：强化max value

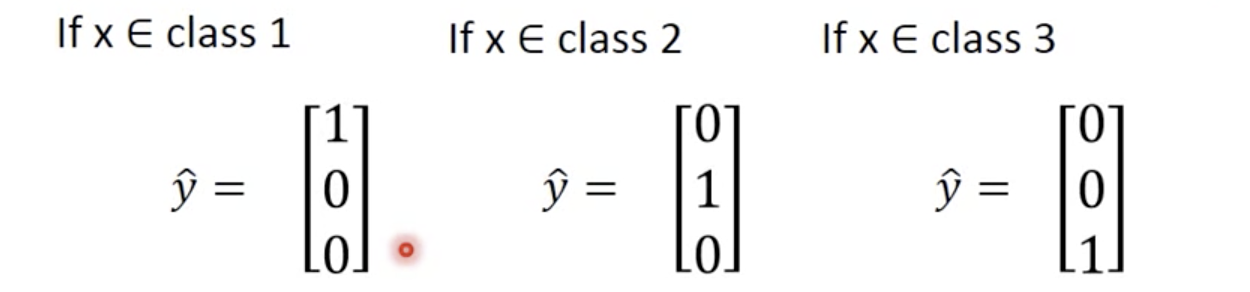
逻辑回归的限制：线性模型

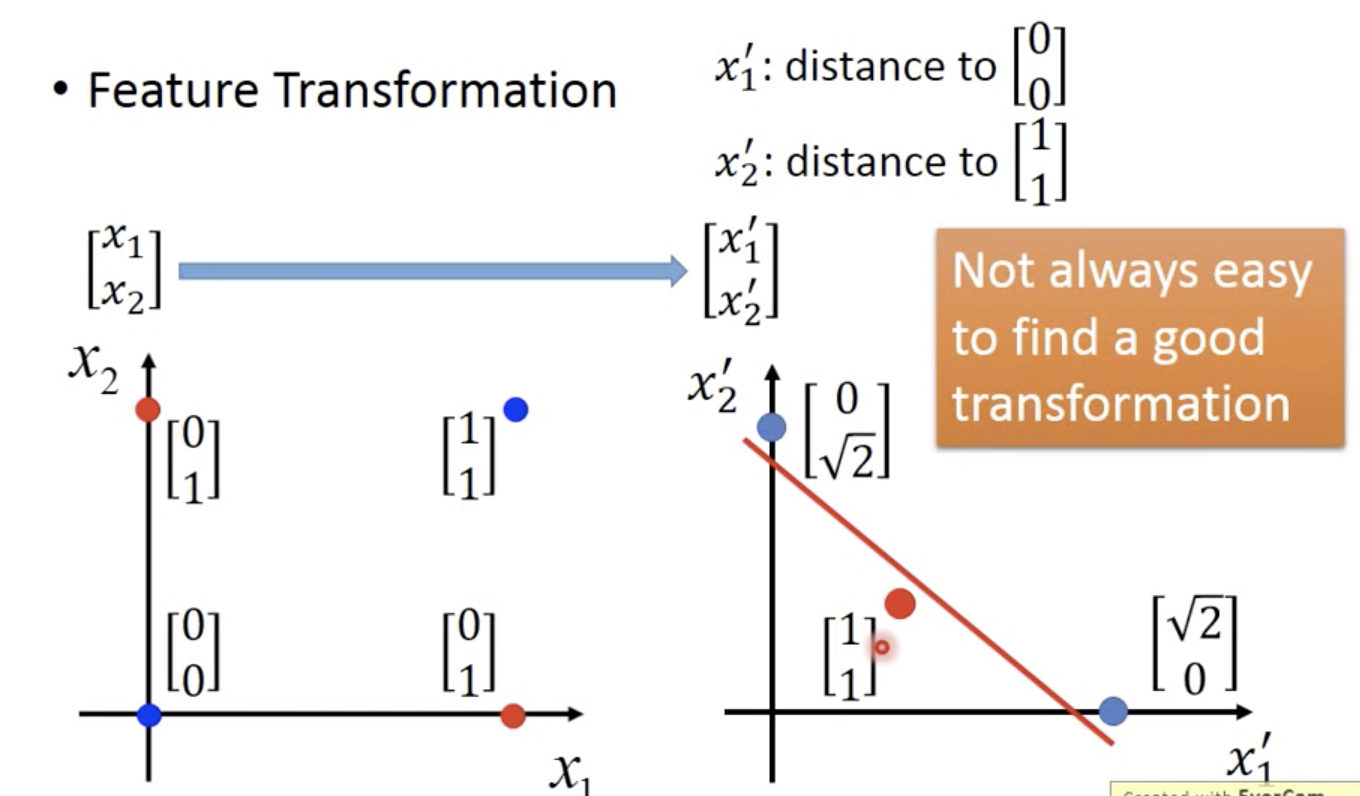
可以进行特征变换，但是很难人工找到特征变换公式

将多个逻辑回归模型级联

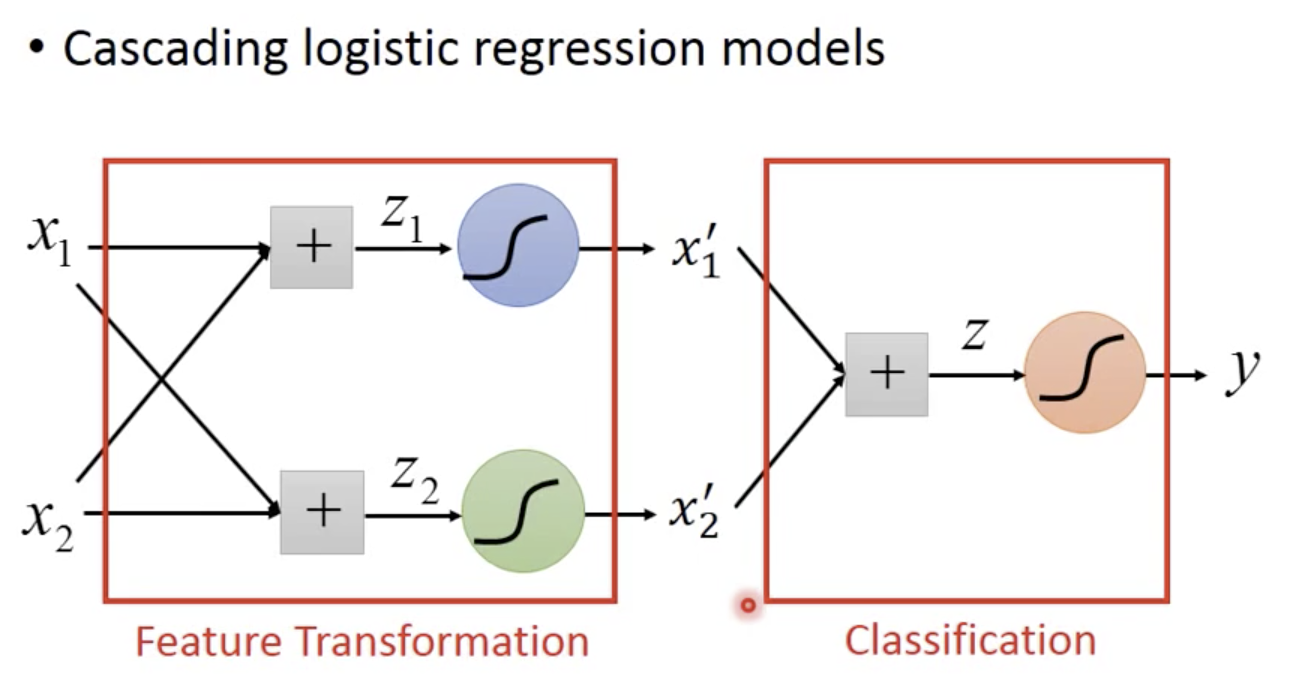
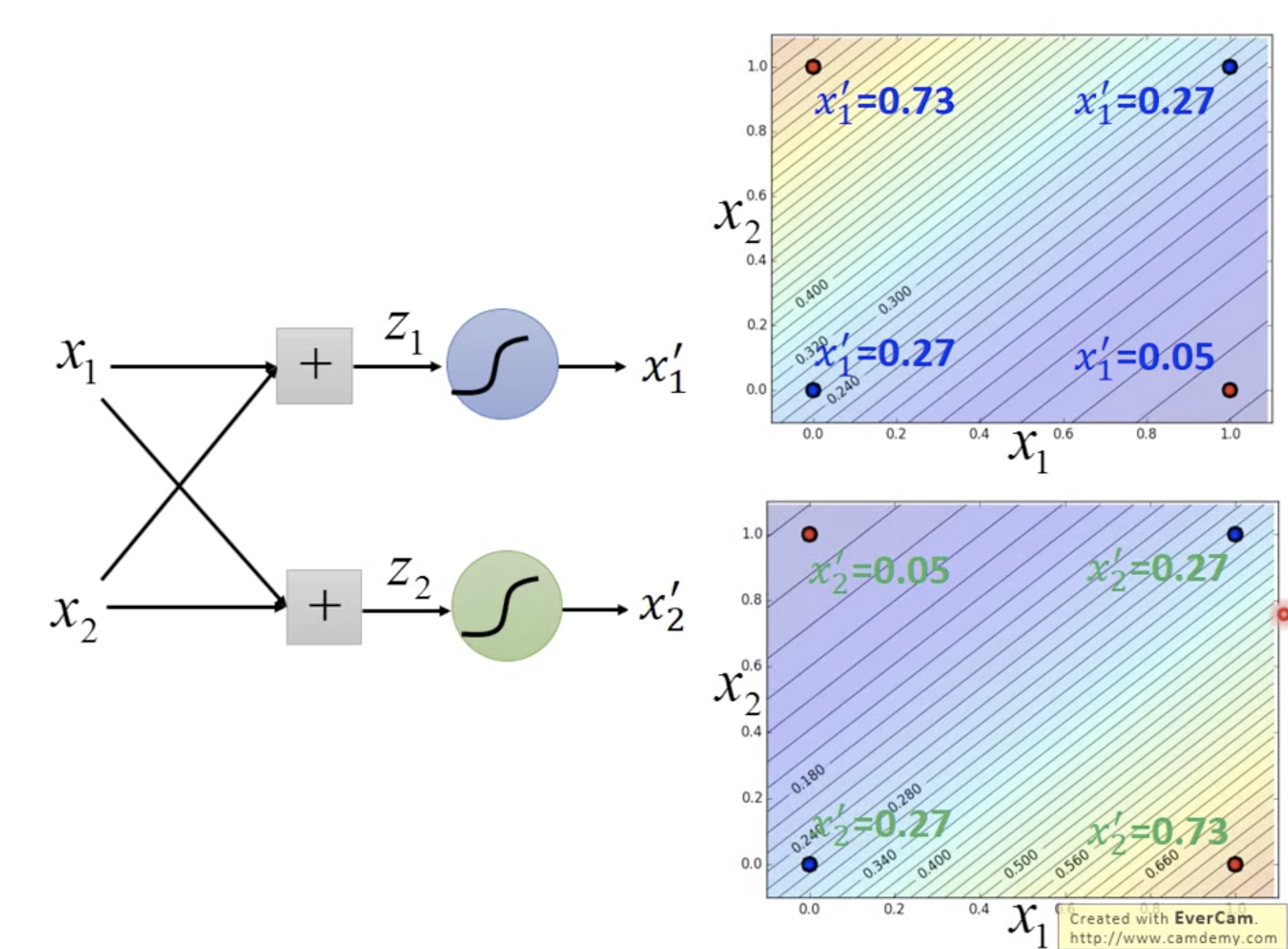
特征转换

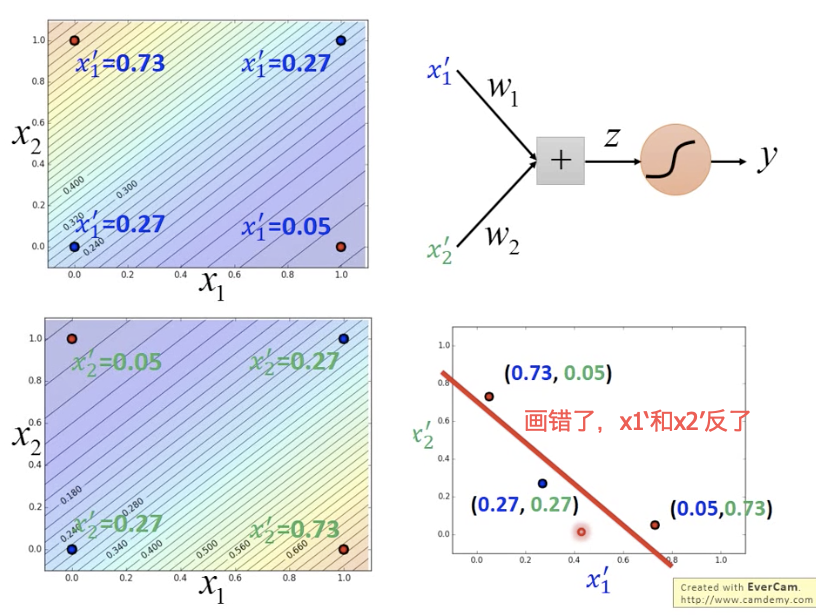
分类