PYYZ 集训

摸底测试 #1

T1-咕咕

给定一个大小为 $N\times M$ 的矩形网格，定义一个合法的路径同时满足以下条件：

路径起点是 $(1,1)$，终点是 $(N,M)$；
$(x,y)$ 只能走到 $(x+1,y)$ 或 $(x,y+1)$；
满足 $T$ 个限制，每个限制都形如：如果走到了 $(a,b)$ 那么下一步一定要走到 $(c,d)$，当 $a=N,b=M$ 的情况不必满足。
求合法路径的数量对 $10^9+7$ 取模的结果。

直接 $dp$，转移时注意限制即可。

点击查看代码

signed main(){

	n=read(),m=read(),t=read();
	while(t--){
		int a=read(),b=read(),c=read(),d=read();
		bool flag=0;
		if(a==n&&b==m)continue;
		if((c==a+1&&d==b)||(d==b+1&&a==c))flag=1;
		
		if(!flag||f[a][b]==-1){
			f[a][b]=-1;
			continue;
		}
		
		if(c==a+1){
			if(f[a][b]==2)f[a][b]=-1;
			else f[a][b]=1;
		}else if(d==b+1){
			if(f[a][b]==1)f[a][b]=-1;
			else f[a][b]=2;
		}
	}
	
	if(f[1][1]==-1){
		puts("0");
		return 0;
	}
	
	dp[1][1]=1;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++){
			if(f[i][j]==-1)dp[i][j]=0;
			else{
				if(f[i-1][j]!=2)dp[i][j]+=dp[i-1][j];
				if(f[i][j-1]!=1)dp[i][j]+=dp[i][j-1];
				dp[i][j]%=p;
			}
		}
		
	println(dp[n][m]);

	return 0;
}

T2-找子串

给定字符串 $S,T$，不断从 $S$ 中删除最靠左的子串 $i$，使得 $i=T$，并将空缺的位置依次向左补齐。

当使用 KMP 从 $S$ 中找 $T$ 时，对于 $S$ 中的每一个位置 $i$，我们记录以 $i$ 结尾的子串和 $T$ 最多匹配到哪里，用 $match$ 数组记录。

e.g. $S$ 为 gogoododgoodluck，$T$ 为 good，则 $match_0=0,match_1=1,match_2=0,match_3=1,match_4=2,match_5=3$。

在上面的例子中，如果将第一个 good 从 $S$ 中删掉后，没必要从头开始找 good，因为之前已经知道 $match_1=1$，所以此时从 $S_1$ 处继续进行 KMP 即可，可以通过栈来维护。

CF148E

第 $i$ 行取出的数字个数一定时，所得到的最大值与其他行无关。

$f_{i,j}$ 第 $i$ 行取 $j$ 个数所能得到的最大和。

CF95E

-------------------------昨晚太颓了，华丽的分割线---------------------------------

摸底测试 #2

T1-江桥的均衡区间【P1360 [USACO07MAR] Gold Balanced Lineup G】

首先考虑 $m=2$ 的情况，分别记下前缀和 $q_{1,i},q_{2,i}$，若存在 $j,i$ 满足 $p_{1,i}-p_{1,j}=p_{2,i}-p_{2,j}$ 就是合法的区间。转化一下，可得 $p_{1,i}-p_{2,i}=p_{1,j}-p_{2,j}$，用 map 记录每个值出现的最早位置即可。

考虑推广，每个能力的前缀和减去这个位置第一种能力的的前缀和做差分就可以得到一个有 $m$ 个值的差分数组。若得到的两个值相等，那么它们就是一个均衡区间，用 map 记录一下每个 vector 出现的最早位置即可。时间复杂度 $\Theta(nm \log n)$。

点击查看代码

int n,m,a[MAXN],qzh[MAXN][MAXM];
std::vector<int> v[MAXN];
std::map<std::vector<int>,int> mp;
 
void init(){
	for(int i=1;i<=n;i++){
		int t=a[i],j=m;
		while(t){
			num[i][j]=t&1;
			t>>=1;
			j--;
		}
	}
	
	for(int i=1;i<=m;i++)
		for(int j=1;j<=n;j++)
			qzh[j][i]=qzh[j-1][i]+num[j][i];
	return;
}

signed main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++)a[i]=read();
	init();
	int ans=0;
	for(int i=1;i<m;i++)v[0].push_back(0);
	for(int i=1;i<=n;i++)
		for(int j=1;j<m;j++)
			v[i].push_back(qzh[i][j+1]-qzh[i][j]);
				
	for(int i=n;i>=0;i--){
		if(mp.count(v[i]))ans=std::max(ans,mp[v[i]]-i);
		else mp[v[i]]=i;
	}
		
	println(ans);
	return 0;
}

T2-江桥洗衣服【P1561 [USACO12JAN] Mountain Climbing S】

贪心，尽可能的荒废将衣服堆积到洗完但未烘干的状态
，这样可以避免多余时间的浪费。

把衣物根据洗和烘干的大小关系将衣物分成两类。

对于洗的时间比烘干时间小的，我们把其都排在另一类的前面，并按洗的时间升序排列，很显然。

对于另一类，我们按照烘干时间长短降序排列，因为考虑烘干慢的可以拖住后面的衣服先洗，以防出现没有衣物洗完烘干机空闲的情况而浪费时间。

按照此策略 $\Theta(n)$ 模拟。

点击查看代码

int n; 
struct node{
	int x,g;
}a[MAXN];

bool cmp(node a,node b){
	if(a.x<a.g){
		if(b.x<b.g)return a.x<b.x;
		else return true;
	}else{
		if(b.x<b.g)return false;
		else return a.g>b.g;
	}
}

signed main(){

	n=read();
	for(int i=1;i<=n;i++)
		a[i].x=read(),a[i].g=read();
	std::sort(a+1,a+n+1,cmp);
	int time_x=0,time_g=0;
	for(int i=1;i<=n;i++){
		time_x+=a[i].x;
		time_g=std::max(time_g,time_x)+a[i].g;
	}
	println(time_g);

	return 0;
}

T3-江桥的三角形围栏【P1715 [USACO16DEC] Lots of Triangles P】

首先考虑部分分，两种做法。

按 $x$ 升序排列各点，$\Theta(n^3)$ 枚举三角形，分讨三角形状态，遍历 $A,C$ 间的所有点，然后求出三边的函数表达式，判断是否在该三角形内。缺点是比较难写。
考虑当一个点 $D$ 在三角形 $ABC$ 中时，连接 $AD,BD,CD$，那么三个小三角形的面积和等于三角形 $ABC$ 的面积。至于面积可以用海伦公式来判断。缺点是有精度误差，易出锅。

接下来考虑正解。

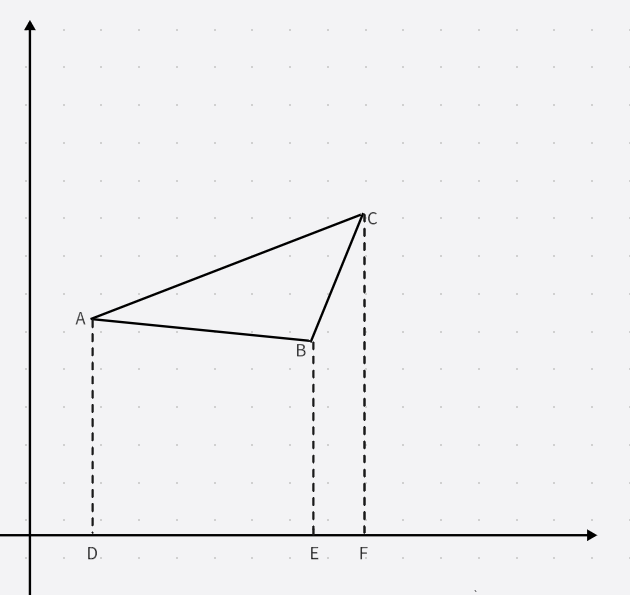
对于图中的三角形 $ABC$，定义 $down_{i,j}$ 为线段 $i,j$ 下所包含的点的数量（例：此图中 $down_{A,C}$ 的值为 $ADFC$ 四边形中包含的点的数量）。利用割补法不难得出答案为 $down_{A,C}-down_{A,B}-down{B,C}$。注意一点，最后答案数量要 $-1$，因为多计入了一个点 $B$。当然，如果线段 $AC$ 下不含点 $B$，那么答案就不需要 $-1$。

点击查看代码

int n,down[MAXN][MAXN],ans[MAXN];
struct node{
	int x,y;
}a[MAXN];

bool cmp(node a,node b){
	if(a.x==b.x)return a.y<b.y;
	else return a.x<b.x; 
} 

int check(int A,int B,int now){
	if(a[now].x<a[A].x||a[now].x>a[B].x)return 0;
	
	double dx=a[B].x-a[A].x;
	double dy=a[B].y-a[A].y;
	double y=dy*(a[now].x-a[A].x)/dx+a[A].y;
	
	return y>a[now].y;
}

signed main(){

	n=read();
	for(int i=1;i<=n;i++)
		a[i].x=read(),a[i].y=read();
	std::sort(a+1,a+n+1,cmp);
	
	for(int A=1;A<n;A++)
		for(int B=A+1;B<=n;B++)
			for(int i=A+1;i<B;i++)
				down[A][B]+=check(A,B,i);
				
	for(int A=1;A<n-1;A++)
		for(int B=A+1;B<n;B++)
			for(int C=B+1;C<=n;C++)
				ans[abs(down[A][C]-down[A][B]-down[B][C]-check(A,C,B))]++;
				
		
	for(int i=0;i<n-2;i++)
		println(ans[i]);
	
	return 0;
}

摸底测试 #3

T1-二元组序列

给定 $a$ 序列，求有多少个二元组 $(i,j)$ 满足 $a_i$&$a_j\le a_i$ ^ $ a_j，i<j$。

比较显然，存在这样一个二元组当且仅当这两个数二进制表示下数位相同。

点击查看代码

int T,n,cnt[55];
int get(int x){
	int t=x,num=0;
	while(t){
		t>>=1;
		num++;
	}
	return num;
}

signed main(){

	T=read();
	while(T--){
		n=read();
		for(int i=1;i<=n;i++){
			int a=read();
			cnt[get(a)]++;
		}
		
		int ans=0;
		for(int i=1;i<=50;i++){
			ans+=(1+cnt[i]-1)*(cnt[i]-1)/2;
			cnt[i]=0;
		}
		println(ans);	
	}

	return 0;
}

T2-攻打恶魔之巅

注意此题不能 $dp$，因为此题具有后效性。

抽象为图论，每个点和其步长范围内的点和可以通过传送门可到达的点连边。$k$ 层分层图最短路，建图跑 $Dijkstra$。

注意到边权为 $0,1$，用 $01bfs$ 解决。

不需要建图，只需要考虑每个的后继即可。

T3-牛牛的灯笼

形式化题面

给定一个序列 $a$，第 $i$ 个位置的权值为 $a_i$，求满足 $\sum\limits_{i=\min(u,v)}^{\max(u,v)}a_i \ge x$ 和 $[\min(u,v),\max(u,v)]$ 区间内不同大小的个数 $\le m$ 的二元组 $(u,v)$ 的个数。

暴力
部分分 #1（$M=N$）

枚举 $u$ 去找 $v$，区间和存在两种情况 $qzh_u-qzh_{v-1},qzh_{v}-qzh_{u-1}$，

基础算法杂题选讲

贪心

CF1612E Messages

当已知方案数 $a_1,a_2,\dots,a_t$ 时，对于每一个 $k_i$，若 $t\le k_i$，当 $a$ 中存在 $k_i$ 对期望的贡献为 $1$，否则为 $0$；当 $t>k_i$ 时，若 $a$ 中存在 $k_i$ 那么对期望贡献为 $\frac{k_i}{t}$，否则为 $0$。

形式化来说，对于选出的 $a_1,a_2,\dots,a_t$，它的期望值为 $\sum\limits_{i=1}{n} [\exists j,m_i=a_j]\frac{\min(k_i,t)}{t}$。

发现每个数之间的贡献独立，枚举 $t$，用桶来统计，取前 $t$ 大。

先给出结论：根据 $\forall k_i \le 20$ 得到最优解的 $t\le 20$。

证明：当 $t\le 20$ 时，$\min(k_i,t)=k_i$，所以 $t$ 的增大与单个数的贡献无关。记 $f_i$ 表示第 $i$ 大的数的贡献，$ans_i$ 表示 $t=i$ 时的答案，则有 $ans_21=\frac{20}{21}ans_20+\frac{f_21}{21}$，因为 $f$ 不增，所以得证。

点击查看代码

int n,m[MAXN],k[MAXN];
std::pair<int,int> sum[MAXN];
std::vector<int> num[MAXN],res;
double ans;

signed main(){

	n=read();
	for(int i=1;i<=n;i++){
		m[i]=read(),k[i]=read();
		num[m[i]].push_back(k[i]);
	}
	
	for(int t=1;t<=20;t++){
		for(int i=1;i<=2e5;i++){
			sum[i].first=0;
			sum[i].second=i;
			for(auto x:num[i])sum[i].first+=std::min(t,x);
		}
		
		std::sort(sum+1,sum+200000+1,std::greater<std::pair<int,int>>());
		
		int cnt=0;
		for(int i=1;i<=t;i++)cnt+=sum[i].first;
		
		double p=cnt/(t*1.0);
		if(p>ans){
			res.clear();
			ans=p;
			for(int i=1;i<=t;i++)res.push_back(sum[i].second);
		}
	}
	
	println(res.size());
	for(int i=0;i<res.size();i++)
		put(res[i],i,res.size()-1);

	return 0;
}

CF1666E Even Split

极差不好求，可以二分答案求最大值和最小值，它们的差是一个答案的下界，问题在于这个下界是否可以取到。

所有可能的方案中，第 $i$ 条线段右端点一定是一个连续的区间。

设 $f_i$ 和 $g_i$ 分别表示第 $i$ 个分界点可能的最小值和最大值。假设我们目前二分的最大值要 $\le maxn$，最小值要 $\ge minn$，那么有转移式：$f_{i+1}=\max(a_{i+1},f_i+minn),g_{i+1}=\min(a_{i+1},g_i+maxn)$。

注意到 $f,g$ 各自的转移相互无关，显然对于第 $i$ 个分界点，可以取 $[f_i,g_i]$ 中的任意一个数，且一定能使极差 $\le maxn-minn$，因此答案下界可取。

倍增与分治

P4155 [SCOI2015] 国旗计划

当是一条链时，可以不断 $dp$，但此题是环，无法破环成链。

需要在未知起点的情况下得到价值。

设 $f_{i,j}$ 从第 $i$ 人开始，一共走了 $2^j$ 步后走到的最远的边防站，直接 $f_{i,j}=f_{f_{i,i-1},j-1}$ 递推即可。

点击查看代码

int n,m;
struct node{
	int l,r;
	int id;
}a[MAXN];
int f[MAXN][25],lst_ans[MAXN];

bool cmp(node x,node y){return x.l<y.l;}

void init(){
	for(int i=1,p=i;i<=2*n;i++){
		while(p<=2*n&&a[p].l<=a[i].r)p++;
		f[i][0]=p-1;
	}
	for(int i=1;i<20;i++)
		for(int j=1;j<=2*n;j++)
			f[j][i]=f[f[j][i-1]][i-1];
			
	return;
}

void solve(int x){
	int lmt=a[x].l+m,ans=1,p=x;
	for(int i=19;i>=0;i--)
		if(f[x][i]!=0&&a[f[x][i]].r<lmt){
			ans+=(1<<i);
			x=f[x][i];
		}
	lst_ans[a[p].id]=ans+1;
}

signed main(){
	
	n=read(),m=read();
	for(int i=1;i<=n;i++){
		a[i].id=i;
		a[i].l=read(),a[i].r=read();
		if(a[i].r<a[i].l)a[i].r+=m;
	}
	
	std::sort(a+1,a+n+1,cmp);
	for(int i=1;i<=n;i++){
		int x=i+n;
		a[x]=a[i];
		a[x].l=a[i].l+m;
		a[x].r=a[i].r+m;	
	}
	
	init();
	for(int i=1;i<=n;i++)solve(i);
	for(int i=1;i<=n;i++)put(lst_ans[i],i,n);

	return 0;
}

CF1523H Hopping Around the Array

倍增+ST表/线段树维护 $\max$。

显然地，若从 $x$ 走 $k$ 步可以到达的最远的点为 $y$，那么我们可以在 $k$ 步以内走到 $[x,y]$ 内的所有点。

考虑 $dp$，设 $dp_{x,i,j}$ 表示从 $x$ 出发，走了 $i$ 步删除了 $j$ 个点后能到的最远点。对于每个询问，都二分找到最小的 $k$。状态数 $\Theta(n^2k)$，不能接受，考虑优化。

$k$ 步能走到的是连续的一段区间，考虑倍增。设 $f_{x,i,j}$ 表示从 $x$ 开始走 $2^i$ 步且删除了 $j$ 个点后能到达的最远的点。转移为 $f_{x,i,j}=\max\limits_{p+q=j} (\max\limits_{y=x}^{f_{x,i-1,p}} dp_{y,i-1,q})$。边界是 $dp_{x,0,j}=\min(x+a_x+j,n)$。然后对于每一层建 $k$ 个 ST 表来维护 $\max$，时间复杂度 $\Theta(nk^2\log n)$。

预处理完后考虑询问，对于每个询问 $(l,r)$，考虑从 $l$ 开始倍增，从大到小枚举 $2^i$，找到最远走不到 $r$ 的最大步数。这个也可以考虑 $dp$ 维护，转移与上面的类似，但每次都需要 $k\log n$ 个 ST 表。发现每次建的 ST 表是一样的，可以离线询问，从大到小枚举 $i$，建出 $f_{x,i,*}$ 的 ST 表，$q$ 个询问可以一起转移。

P8163 [JOI 2022 Final] 铁路旅行 2 (Railway Trip 2)

[AGC046D] Secret Passage

P7883 平面最近点对（加强加强版）

考虑分治，用一条中轴线拆分平面，向下递归，找到左右平面内的最近点对长度为 $d$。

还要统计横跨中轴线的点对。首先这两个点必须满足离中轴线距离 $\le d$。为了使答案更优，一个点只可能与 $d\times 2d$ 矩形内的点形成最近点对，而这个矩阵中点的个数并不多，因为如果点数过多的话一侧的最近点对答案就不会为 $d$，因此分治两边+暴力检验中轴线即可。

[AGC002D] Stamp Rally

一次询问可以二分+并查集。

多次询问并查集维护（答案上界为并查集内的点数，下界为 $x$ 和 $y$ 之间的最短路）+整体二分

构造

CFgym105214K

CF1764G3 Doremy's Perfect DS Class (Hard Version)

首先当 $k=2$ 时，若 $n$ 为奇数，那么此时只有 $1$ 自己一个人一组。所以我们考虑对于每个位置 $i$，查询 $[1,i-1]$ 和 $[1,i]$ 的答案，如果答案一样那么这个位置肯定不是 $1$

杂题

CF1627F Not Splitting

分界线一定是一个中心对称图形，分成的两个部分也一定中心对称，且这条分界线一定过中心点。

当所有点都在矩阵一边时，我们直接求中线点到矩阵一边的最短路然后对称即可。当遍布点对时，我们在和每个点对对称的位置复制一遍这个点对，然后再求最短路，最后对称即可。

[ARC115D] Odd Degree

CF643G Choosing Ads

CF1439B Graph Subset Problem

UOJ750【UNR #6】小火车

树上问题

树的直径

树的直径为树上最远两点的距离，又称为树上最长链

树形 DP

设 $1$ 号节点为根，转化有根树；设 $d_x$ 为从节点 $x$ 出发走向以 $x$ 为根的子树中可以到达的最远距离，转移为 $d_x=\max\limits_{y_i\in son_x}{d_{y_i}+edge(x,y_i)}$。

设 $F_x$ 为经过 $x$ 节点的最长链的长度，则有 $F_x=\max\limits_{y_i\in son_x,y_j\in son_x}{d_{y_i}+d_{y_j}+edge(x,y_i)+edge(x,y_j)}$。

考虑复杂度，最坏会到达 $\Theta(n^2)$。其实并不需要枚举两个变量，可以在求 $d_x$ 的时候就计算出 $F_x$ 的值，即可以枚举儿子更新 $ans$，然后再去更新 $d_x$。

点击查看代码

void DP(int x){
	vis[x]=1;
	for(auto i:vec[x]){
		int y=i.first,d=i.second;
		if(vis[y])continue;
		DP(y);
		ans=std::max(ans,d[x]+d[y]+d);
		d[x]=std::max(d[x],d[y]+d);
	}
}

贪心

两遍 DFS。第一次从 $1$ 号节点出发，找到距离 $1$ 号节点最远的点，记作 $p$；第二遍从 $p$ 节点出发，找到距离 $p$ 节点最远的点，记作 $q$。那么 $p,q$ 之间的距离就是树的直径。

P3629 [APIO2010] 巡逻

当 $k=0$ 时，树上的每条边都会至少遍历一次，再回到 $1$ 号节点会恰好经过每条边两次，路线总长度为 $2(n-1)$。

当 $k=1$ 时，因为新道路必须只经过起一次，所以会形成一个环，所以我们找到树的最长链，在这两个节点之间连边，则答案为 $2(n-1)-l+1$，$L$ 为树的直径。

当 $k=2$ 时，图上又会新增一个环。当两个环不重叠时，答案同上的计算方式再减小一部分。否则，两个环的重叠部分会由“只需经过一次”变回“需要经过两次”。

实现步骤如下：

原图上求直径，记为 $L_1$，并将直径边取反；
再求一次直径，记为 $L_2$。

因此最终的答案为 $2(n-1)-(L_1-1)-(L_2-1)=2n-L_1-L_2$，因为我们取反了，所以答案不会在两环重叠的情况下出错。

注：本题第一次求直径时，边权均为非负并且要求出具体的路径，适合用两遍 BFS 来解决；第二次求直径时，边权可能为负数并且只需要求出直径长度，所以适合用树形 DP。

P1099 [NOIP2007 提高组] 树网的核

简化题意：给定一棵带边权无根树，在其直径上求出一段长度不超过 $s$ 的路径 $F$，使得离路径距离最远的点到路径的距离最短。

解法一：枚举 $\Theta(n^3)$

先通过两次 BFS 求出任意一条直径（最长链），然后枚举链上的两点 $p,q$，要求 $p,q$ 间的距离不超过 $s$，$p,q$ 两点之间的路径叫做树网的核。从核上的额每个点向外 DFS，求核外每个点距离，最大值则为核的偏心距。在所有枚举的核中取最小值，就是最小偏心距。

解法二：枚举+贪心 $\Theta(n^2)$

根据贪心策略，当树网核的一端 $p$ 固定以后，另一端的 $q$ 显然实在合法条件下越远越好（因为此时可以扩大核的范围，使偏心距最小）。因此，我们只需要在直径上枚举 $p$，然后直接确定 $q$ 点位置即可，时间复杂度降低到 $\Theta(n^2)$。

解法三：二分答案 $\Theta(n\log SUM)$

本题答案具有单调性，可以将问题转化为“验证是否存在一个核，使得其偏心距不超过二分的值 $mid$”。

设直径的两个端点为 $u,v$，在直径上分别找出和 $u,v$ 距离不超过 $mid$ 的最远点 $p,q$。根据直径的最长性，不难发现 $p,q$ 一定是满足偏心距为 $mid$ 且最靠近树网中心的点对。

接下来，我们需要检查 $p,q$ 间的距离是否不超过 $s$，同时用 DFS 检查把 $p,q$ 之间的路径作为树网的核时，离核最远的点的距离是否不超过 $mid$，若全满足则 $p,q$ 间的路径就是偏心距不超过 $mid$ 的一个合法的核。

解法四：分析性质，直接扫描 $\Theta(n)$

LCA

P3379 【模板】最近公共祖先（LCA）

$LCA(x,y)$ 是 $x$ 到根的路径和 $y$ 到根的路径的交汇点，是 $x,y$ 之间路径上深度最小的节点。

向上标记法

从 $x$ 向上走到根节点，并标记所有经过的节点。从 $y$ 向上走到根节点，当第一次遇到已标记的节点时，就找到了 $LCA(x,y)$。对于每次询问最差为 $\Theta(n)$。

树上倍增法

设 $F_{x,k}$ 表示 $x$ 的 $2^k$ 辈祖先，若节点不存在则赋值为 $0$，$F_{x,0}$ 是 $x$ 的父亲。此外，$\forall k\in [1,\log n]，F_{x,k}=F_{F_{x,k-1},k-1}$。

预处理时间复杂度为 $O(n \log n)$。

对于 $LCA(x,y)$ 的具体运算，分为以下几步：

设 $d_x$ 表示 $x$ 的深度，不妨设 $d_x \le d_y$;
用二进制拆分思想，把 $x$ 调整到和 $y$ 的同一深度;
若 $x=y$ 则结束进程，$LCA(x,y)=y$；
同时用二进制思想，倍增向上调整，若 $f_{x,k}\not=f_{y,k}$，则令 $x=F_{x,k},y=F_{y,k}$；
此时 $p,q$ 两点离相会点都为 $1$，答案为它们的父节点。

Tarjan 求 LCA

P1967 [NOIP2013 提高组] 货车运输

我们的目的是，让连通性保持不变的情况下，最小值最大，显然是要求最大生成树。
记录 $x,y$ 路径中的最小值，它就是限重，我们可以让 $x,y$ 向上找 LCA，过程中维护最小值。

dfs 序

概念

时间戳

在树的 DFS 中，以每个节点第一次被访问的顺序，依次给予 $n$ 个节点。$dfn_i$ 表示 $i$ 的时间戳，即 $i$ 在 DFS 遍历中第 $dfn_i$ 个被访问到。

树的 DFS 序

在树的 DFS 遍历中，对于每个节点进入递归后以及即将回溯前各记录一次节点的编号，这个长度为 $2n$ 的序列就是树的 DFS 序。

具有以下性质：

每个节点在序列中恰好出现 $2$ 次。
设 $L_x,R_x$ 表示 $x$ 出现的两次位置，那么 $[L_x,R_x]$ 表示以 $x$ 为根的一棵子树。

LOJ#144. DFS序 1

首先求出树的 DFS 序，在序列上进行单点加和区间查询，树状数组解决即可。

LOJ#145. DFS序 2

相当于在 DFS 序上进行区间加和区间查询，树状数组（树状数组也可以区间查询区间修改，见下）或带懒标记的线段树。

扩展：

AcWing243 一个简单的整数问题2

树状数组的区间加和区间查询，《算进》P229。

LOJ#146. DFS 序 3，树上差分 1

共三种操作：路径权值加，单点询问，子树（区间）求和

DP

所有 dp 都要考虑拆分区间和合并区间。

树上 DP

可以分为：从根往叶子 dp、从叶子往根 dp 和换根 dp。

P3267 [JLOI2016/SHOI2016] 侦察守卫

设两个 dp 数组。$f_{x,i}$ 表示包含以 $x$ 为根的子树中所有的关键点的前提下，至少还可以向 $x$ 父亲方向覆盖 $i$ 个点的最小代价；$g_{x,i}$ 表示往下距离 $x$ 点深度 $i$ 的所有关键点被覆盖的前提下，剩下距离 $x$ 点不超过 $i$ 的是否覆盖随意的情况下的最小代价。

设 $v$ 为 $u$ 的子节点，则有两个基本的转移方程：$f_{u,i}=\min(f_{u,i}+g_{v,i},g_{u,i+1}+f_{v,i+1}),g_{u,i}=\sum g_{v,i-1}$。

根据状态的定义，还可以得到以下两个转移式：$f_{u,i}=\min(f_{u,i},f_{u,i+1}),g_{u,i}=\min(g_{u,i},g_{u,i-1})$。

此时，我们需要区分一下关键点和普通点的初始状态。因为关键点必选，普通点可以不选，所以可以得到转移方程：$x\in 关键点,f_{x,0}=w_x$ 和 $y\in 普通点,f_{y,0}=0$。除此之外，无论是关键点还是普通点，初始情况下要覆盖其他点时一定说明我们在这里建了一个哨站。所以 $\forall i,0\le i < n f_{x,i}=w_x$。

当转移合并子树时，我们先算 $f$ 后算 $g$。

点击查看代码

int n,d,m,w[MAXN];
int f[MAXN][25],g[MAXN][25];
bool vis[MAXN];
std::vector<int> vec[MAXN];

void add(int u,int v){
	vec[u].push_back(v);
	vec[v].push_back(u);
}

void dfs(int x,int fa){
    if(vis[x])f[x][0]=g[x][0]=w[x];
    else{
		f[x][0]=0;
		g[x][0]=0;
	}
	
    for(int i=1;i<=d;i++)f[x][i]=w[x];
    for(int i=0;i<vec[x].size();i++)
    	if(vec[x][i]!=fa)dfs(vec[x][i],x);


    for(int i=0;i<vec[x].size();i++){
        int u=vec[x][i];
        if(u==fa)continue;
        
        for(int j=d;j>=0;j--)
            f[x][j]=std::min(std::min(f[x][j]+g[u][j],g[x][j+1]+f[u][j+1]),f[x][j]+f[u][j+1]);
        
        for(int j=d;j>=0;j--)f[x][j]=std::min(f[x][j+1],f[x][j]);
        
        g[x][0]=f[x][0];
        for(int j=1;j<=d+1;j++)
            g[x][j]=g[x][j]+g[u][j-1];
        for(int j=1;j<=d+1;j++)
            g[x][j]=std::min(g[x][j],g[x][j-1]);
    }
    
    for(int j=d;j>=0;j--)
        f[x][j]=std::min(f[x][j+1],f[x][j]);
    for(int j=1;j<=d+1;j++)
        g[x][j]=std::min(g[x][j],g[x][j-1]);
}

signed main(){

	n=read(),d=read();
	for(int i=1;i<=n;i++)w[i]=read();
	m=read();
	for(int i=1;i<=m;i++){
		int x=read();
		vis[x]=1;
	}
	
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		add(u,v);
	}
	
	memset(f,0x3f,sizeof(f));
	
	dfs(1,0);
	int minn=LLONG_MAX;
	for(int i=0;i<=d;i++)
		minn=std::min(minn,f[1][i]);
	println(minn);

	return 0;
}

区间 DP

将一个区间拆分为若干个相互无联系的区间时，我们的重点时找到一种方式使得区间互相不关联。

CF607B Zuma

$\forall k,l\le k<r,f_{l,r}=\min(f_{l,k},f_{k+1,r})$;
当 $a_l=a_r$ 时，$f_{l,r}=f_{l+1,r-1}$。

点击查看代码

int n,a[505],dp[505][505];

signed main(){

	n=read();
	for(int i=1;i<=n;i++)a[i]=read();
	memset(dp,0x3f,sizeof(dp));
	
	for(int i=1;i<=n;i++)dp[i][i]=1;
	for(int i=1;i<n;i++){
		if(a[i]!=a[i+1])dp[i][i+1]=2;
		else dp[i][i+1]=1; 
	} 
	
	for(int i=3;i<=n;i++)//长度 
		for(int j=1;i+j-1<=n;j++){
			int l=j,r=i+j-1;
			if(a[l]==a[r])dp[l][r]=dp[l+1][r-1];
			for(int k=l;k<r;k++)
				dp[l][r]=std::min(dp[l][r],dp[l][k]+dp[k+1][r]);
		}
		
	println(dp[1][n]);

	return 0;
}

[AGC039E] Pairing Points

注意到一个事实：如果此时已经存在了一个交点，那么下面的边就不能再穿过这个交点了。

我们考虑破环为链，从 $1$ 号点断开，枚举 $1$ 号点连接的点，然后可以让 $(2,2n)$ 这些点断开。我们设 $f_{i,j,k}$ 表示区间 $[i,j]$ 中的点 $k$ 向外连接了一条边。答案是枚举 $1$ 号点连接的点，即 $\sum\limits_{i=3}^{2n-1} f_{2,2n,i}$。

考虑求 $f_{i,j,k}$。因为要求边联通，所以与 $k$ 相连的边必然被 $[i,j]$ 中的某两个点所连接的边穿过。考虑枚举最靠外的边，记为 $(x,y)$，所以这个区间会被分成 $[i,k,x]$ 和 $[k,j,y]$ 两部分。但是因为 $[x,k]$ 和 $[k,y]$ 之间仍然可能出现连边，所以问题并未解决。

发现，在 $[i,k]$ 中一定存在一个分界线，使得分界线两侧互不相连。不妨再次枚举分界线，设为 $p,q$，因此区间再次被分为三个部分：$[i,p,x],[p,q,k],[q,j,y]$，不难发现此时三个部分之间没有连边，于是成功将区间拆分。

点击查看代码

int n,a[MAXN][MAXN];
char c[MAXN];
int f[MAXN][MAXN][MAXN];
bool vis[MAXN][MAXN][MAXN];

int DP(int l,int m,int r){
	if(l==m&&r==m)return 1;
	if((l^r)&1||(l==m||r==m))return 0;
	
	if(vis[l][m][r])return f[l][m][r];
	vis[l][m][r]=1;
	
	for(int p=l;p<m;p++)
		for(int q=r;q>m;q--)
			if(a[p][q])
				for(int x=p;x<m;x++)
					for(int y=q;y>m;y--)
						f[l][m][r]+=DP(l,p,x)*DP(y,q,r)*DP(x+1,m,y-1);
						
	return f[l][m][r];
}

signed main(){

	n=read();
	n<<=1;
	for(int i=1;i<=n;i++){
		std::cin>>c+1;
		int l=strlen(c+1);
		for(int j=1;j<=n;j++)a[i][j]=(int)(c[j]&1);
	}
	
	int ans=0;
	for(int i=2;i<=n;i++)
		if(a[1][i])ans+=DP(2,i,n);
		
	println(ans);

	return 0;
}

P5985 [PA2019] Muzyka pop

[AGC035D] Add and Remove

首先第一眼考虑区间 dp，但是存在一个区间 $[l,r]$ 中间删掉一个点 $p$ 后，$[l,p-1]$ 和 $[p+1,r]$ 拼起来后仍然会相互影响的情况。

换一种方式，我们找到 $[l+1,r-1]$ 中最后删除的点 $p$，这样区间 $[l,r]$ 的答案就是最终三个数的答案。好处是我们发现删除 $[l+1,p-1]$ 的时候，对 $p$ 产生的贡献和删除 $[p+1,r-1]$ 的时候对 $p$ 的贡献是完全独立的，可以分开。

再看每个位置的贡献，考虑对答案贡献的倍数。设 $a_l$ 贡献了 $x$ 倍，$a_r$ 贡献了 $y$ 倍。由于 $a_p$ 会两边都贡献到，所以 $a_p$ 会对答案贡献 $x+y$ 倍。

设 $f_{l,r,x,y}$ 表示删除 $[l+1，r-1]$ 后，$xa_l+ya_l$ 的最小值，不难得到转移 $f_{l,r,x,y}=\min{f_{l,p,x,x+y}+f_{p,r,x+y,y}+(x+y)a_p}$。

计算一下复杂度，前两维肯定是 $n^2$ 的空间复杂度，后两维表示每次向下会由两个转移而来，最多转移 $n$ 层，需要 $2^n$ 的空间。因此时间复杂度不会超过 $\Theta(n^3 2^n)$（好像经过一些奇怪的计算会发现它不会超过 $\Theta(2^n)$ 的）。

点击查看代码

int n,a[MAXN];
int dfs(int l,int r,int x,int y){
	if(r-l<=1)return 0;
	int minn=LLONG_MAX;
	
	for(int i=l+1;i<=r-1;i++)
		minn=std::min(minn,dfs(l,i,x,x+y)+dfs(i,r,x+y,y)+(x+y)*a[i]);
		
	return minn;
}

signed main(){

	n=read();
	for(int i=1;i<=n;i++)
		a[i]=read();
		
	println(a[1]+a[n]+dfs(1,n,1,1));

	return 0;
}

背包 DP

CF1442D Sum

首先注意到一个性质：之多有一个序列只选择了一部分，剩下的序列要么都选，要么都不选。证明比较显然。

我们可以把每个序列都看做一个物品，价值是序列和，重量是序列长度。

枚举没有被选满的序列，以及具体选到了哪里，可以把问题转化为“有 $n$ 个物品，对 $i=1,2,\dots,n$，需要求出去掉第 $i$ 个物品后，对其他物品做背包的结果”。

普通背包复杂度 $\Theta(nk)$，枚举 $i$ 的复杂度 $\Theta(n)$，总复杂度 $\Theta(n^2k)$，不可接受。

考虑分治算法。

对于区间 $[l,r]$，找到一个中点 $mid$。先将 $[l,mid]$ 中的物品放到背包中，然后 solve(mid+1,r)。将背包还原，再将 $[mid+1,r]$ 的物品插入到背包中，然后 $solve(l,mid)。最终，当 $l=r$ 时就会得到我们想要的答案。

时间复杂度 $\Theta（nk\log n）$。

状压 DP

P6192 【模板】最小斯坦纳树

P7142 [THUPC2021 初赛] 密集子图

线头 DP

CF626F Group Projects

P7163 [COCI2020-2021#2] Svjetlo

DP 杂题

P2467 [SDOI2010] 地精部落

如果是普通的序列我们可以 dp，设 $f_{i,j,0/1}$ 表示选到 $i$，数值为 $j$，是否是山峰，转移也比较显然，我们根据题意枚举符合条件的 $k$，可以转移到 $f_{i+1,k,0/1}$。

但是排列要求不重不漏。设 $f_{i,j,0/1}$ 表示第 $i$ 个数是前面第 $j$ 小的，是不是山峰。同样可以枚举合法的 $k$，转移到 $f_{i+1,k,0/1}$。复杂度 $\Theta(n^3)$，可以用前缀和优化第二维使复杂度降至 $\Theta(n^2)$。

另外一种做法是设 $f_{i,j},g_{i,j}$ 分别表示长度为 $i$ 开头为山峰/山谷且高度为 $j$ 的方案数。

我们可以先插入一个数，如果是山峰，那原本所有 $\ge j$ 的数都向上平移一格，可以得到 $f_{i,j}=\sum\limits_{k=1}^{j-1} g_{i-1,k}=\sum\limits_{k=1}^{j-1} f_{i-1,i-k}$。

P5228 [AHOI2013] 找硬币

相当于确定一个新进制序列 $k$，$k_i$ 表示第 $i$ 位满 $k_i$ 进位，求所有数位之和。

不难发现此题 $k_i$ 不可能是合数，转化为质数肯定更优。

注意有几个性质：

每个数的不同质因子的个数不会很多；
调和级数：$H_n=\sum\limits_{i=1}^n \frac{1}{n}$，它的是 $\log n$ 级别的；
$\lfloor\frac{\lfloor\frac{n}{m}\rfloor}{k}\rfloor=\lfloor{\frac{n}{mk}}\rfloor$。

设 $f_{i,M}$ 表示考虑到第 $i$ 位，前面质因子的乘积为 $M$

[AGC061C] First Come First Serve

[ABC290Ex] Bow Meow Optimization

[ARC134E] Modulo Nim

P1758 [NOI2009] 管道取珠

训练赛 #1

T1-三角形的面积

给定平面上的 $n$ 个点，问其组成的三角形面积为整数的三角形的个数。

我们考虑一个三角形的面积，因为不保证它与坐标轴平行，所以我们考虑最朴素的做法：割补法。矩形的面积一定是整数，我们只需考虑割掉的三个小三角形的面积情况。因此我们只需要存下每个点的奇偶性，然后排列组合计算即可。

点击查看代码

int n,num[5][5];

signed main(){

	n=read();
	for(int i=1;i<=n;i++){
		int x=read(),y=read();
		num[x&1][y&1]++;
	}
	
	int ans=n*(n-1)*(n-2)/6;
	ans-=(num[0][1]*num[0][0]*num[1][0]);
	ans-=(num[0][1]*num[1][0]*num[1][1]);
	ans-=(num[0][1]*num[0][0]*num[1][1]);
	ans-=(num[0][0]*num[1][0]*num[1][1]);
	
	println(ans); 

	return 0;
}

T2-完全背包问题

有 $n+1$ 种物品，体积分别为 $0,1,\dots,n$，价值分别为 $w_0,w_1,\dots,w_n$，每种物品的数量都是无限的。$m$ 个询问，给出 $k,v$，表示需要选择恰好 $k$ 个物品，使得总体积恰好为 $v$，求最大总价值。

DP 背包

设 $dp_{i,j}$ 表示选择了 $i$ 个物品，体积为 $j$ 的最大价值。暴力枚举下一个物品进行转移到 $dp_{i+1,k}$。

点击查看代码

int n,m,w[5005],d[5005];
int dp[5005][5005];//i 物品，j 体积 

signed main(){

	n=read(),m=read();
	for(int i=0;i<=n;i++){
		w[i]=read();
		dp[1][i]=w[i];
	}

	for(int i=2;i<=n;i++)
		for(int j=0;j<=n;j++)
			for(int k=0;k<=j;k++)
				dp[i][j]=std::max(dp[i][j],dp[i-1][j-k]+w[k]);

	int ans=0;
	for(int i=1;i<=n;i++)
		for(int j=0;j<=n;j++)
			ans+=dp[i][j]^i^j;
	
	while(m--){
		int k=read(),v=read();
		if(k==0)println(ans);
		else println(dp[k][v]);
	}
	

	return 0;
}

优化【根号】

$dp_{i,j+k}=\max{dp_{i,j+k},dp_{i-1,j}+w_k}$，滚动数组把第一维滚掉，得到 $dp_{i}=\max{dp_{j}+w_{i-j}}$。

定义某种运算 $c=a\otimes b$，代表 $c_i=a_j+b_{i-j}$，此运算具有结合律。

单次计算 $dp_i$ 时间复杂度为 $\Theta(n^2)$。

根据结合律，设 $K=\lceil \sqrt{n}\rceil$，则 $f_i=f_{\lfloor \frac{i}{K}\rfloor K} \otimes f_{i\mod K}$。因此，对于每一层，我们只需要预处理 $dp_0,dp_1,\dots,dp_K$ 和 $dp_K,dp_{2K},\dots,dp_{K^2}$，询问用 $\Theta(n)$ 的时间计算 $dp_{k,v}$。

(包哥说这是群论和卷积以及光速幂/jk/jk/jk)

正解

$100$ 比 $80$ 简单/jy

设 $dp_{i,j,k}$ 表示考虑了体积为 $[i,n]$ 的物品，选了 $j$ 个物品，总体积为 $k$ 的最大价值。转移为 $dp_{i,j,k}=\max(dp_{i+1,j,k},dp_{i,j-1,k-i}+v_i)$，因为我们所有考虑过的物品体积至少为 $i$，因此 $j\le \frac{n}{i}$，时间复杂度为 $\Theta(m+n(\frac{n}{1}+\frac{n}{2}+\dots+\frac{n}{n}))=\Theta(n^2\log n+m)$。

可以滚掉第一维，降低空间复杂度。

点击查看代码

int n,m,w[MAXN];
int op,v;
int dp[MAXN][MAXN];

signed main(){

	n=read(),m=read();
	for(int i=0;i<=n;i++)w[i]=read();
	for(int i=0;i<=n;i++)
		for(int j=0;j<=n;j++)
			dp[i][j]=-LLONG_MAX;

	dp[0][0]=0;
	for(int i=n;i>=0;i--){
		int lim;
		if(i==0)lim=n;
		else lim=n/i;
		
		for(int j=1;j<=lim;j++)
			for(int k=i;k<=n;k++)
				dp[j][k]=std::max(dp[j][k],dp[j-1][k-i]+w[i]);
	}
	
	int ans=0;
	for(int i=1;i<=n;i++)
		for(int j=0;j<=n;j++)
			ans+=dp[i][j]^i^j;
			
	while(m--){
		op=read(),v=read();
		if(op!=0)println(dp[op][v]);
		else println(ans);
	}
	return 0;
}

T3-子集询问

给定 $n$ 个整数，一个每个数的范围为 $[1,m]$，有 $q$ 条信息，每条信息是下面的两种之一：某几个数的最小值/最大值在 $[l,r]$ 内。求区间的最小可能值和最大可能值。

可以暴力枚举每个数字所有 $m$ 种可能的取值，判断其是否合法，复杂度 $\Theta(qm^n)$。

考虑优化。$\Theta(n!)$ 枚举所有可能的排列，得到一个升序的序列，在 $O(2^n)$ 的时间内得到解。

T4-寻找宝藏

给定 $n$ 个数对 $(p_i,v_i)$ 和一个整数 $k$，求对于每个长度为 $k$ 的区间 $[l,l+k-1]$，不考虑该区间内的数对时，剩下数对里 $p$ 值不降的子序列的 $v$ 总和的最大值。

只会 $60$ 分。设 $f_i$ 表示考虑前 $i$ 个数且选择了 $i$ 的情况下 $v$ 总和的最大值，不难得到转移 $f_i=\max(f_j)+v_i$，其中 $1\le j <i,p_j\le p_i$，可以用树状数组优化 DP 的转移，复杂度 $\Theta(n^2\log n)$。

点击查看代码

int n,k,x[MAXN],v[MAXN];
int dp[MAXN];
int c[MAXN*10];

void init(){
	for(int i=1;i<=n*10;i++)c[i]=0;
	for(int i=1;i<=n;i++)dp[i]=0;
}

int query(int x){
	int maxn=0;
	for(int i=x;i;i-=(i&(-i)))maxn=std::max(maxn,c[i]);
	return maxn;
} 

void update(int a,int b){
	for(int i=a;i<=n;i+=(i&(-i)))c[i]=std::max(c[i],b); 
}

signed main(){
	
	n=read(),k=read();
	for(int i=1;i<=n;i++)
		x[i]=read(),v[i]=read();
		
	for(int l=1;l+k-1<=n;l++){
		int r=l+k-1;
		init();
		
		int maxn=0;
		for(int i=1;i<=n;i++){
			dp[i]=query(x[i]);
			if(!(l<=i&&i<=r))dp[i]+=v[i];
			maxn=std::max(maxn,dp[i]);
			update(x[i],dp[i]);
		}
		println(maxn);
	}

	return 0;
}

组合数学及计数

组合数学

出门左转

计数技巧

常见方法：捆绑法，插空伐，隔板法。

捆绑法

将要求相邻的若干相邻的物品视为一个整体来进行计数。注意考虑整体内部的相对顺序。

插空法

若要求若干物品两两不相邻，可以先将其他物品放好，然后将这些物品插入空中来进行计数。

隔板法

可以将不可区分物品分配问题/不定方程整数解问题转化为插板组合问题

水题 $19$ 道选讲

Problem $1$

一个平面内有 $8$ 个点，只有 $4$ 点共圆，其余任何 $4$ 点不共圆，求这 $8$ 点可以确定的最多的圆的数量。

因为三点共圆，所以本来有 $C_8^3$ 个圆，但由于存在 $4$ 点共圆，即该圆被统计了 $C_4^3$，所以需要扣掉，同时四点共圆的圆被扣完了，还要加上一次。答案为 $C_8^3-C_4^3+1$。

Problem $2$

求从集合 ${1,2,\dots,n}$ 中取 $r$ 个不相邻的元素的方案数。

隔板法。考虑 $n-r$ 个元素，形成了 $n-r+1$ 个空位（此题两端也可以放），插入 $r$ 个隔板，把隔板视为元素，注意到每种插入方法抢号对应了一种选择方案。答案为 $C_{n-r+1}^r$。

Problem $3$

网格图上从 $(0,0)$ 走到 $(n,m)$，每次只能向上或向右走一步，求方案数。

注意到我们一定只能走 $n+m$ 步，只需要看哪些步是向上走的即可。答案为 $C_{m+n}^m$。

Problem $4$

有甲乙丙丁戊 $5$ 个神仙排成一排，要求甲必须站在乙的左边，求方案数。

不难发现甲要不站在乙的左边，要么站在乙的右边，只存在两种情况，所以答案为 $\frac{A_5^5}{2}$。

训练赛 #2

T1-剑的比试【[ABC297D] Count Subtractions】

类似求 $\gcd$ 的方法，取模、整除维护答案即可。

点击查看代码

signed main(){
    
    int T=read();
	while(T--){
		int a=read(),b=read();
		int ans=0;
		while(a!=b){
			if(a>b){
				if(a%b==0){
					ans+=a/b-1;
					break;
				}
				else{
					ans+=a/b;
					a=a%b;
				}
			}else{
				if(b%a==0){
					ans+=b/a-1; 
					break;
				}
				else{
					ans+=b/a;
					b=b%a;
				}
			}
		}
		println(ans);
	}

	return 0;
}

T2-顽皮的猴子【CF587C Duff in the Army】

有 $n$ 座山，形成了了一棵树。有 $m$ 只猴子，分别居住在 $c_1,c_2,\dots,c_m$ 座山上。求从 $u$ 到 $v$ 的最短路径上猴子的数量和前 $k$ 小的节点的编号。

$20$ pts

对于每次询问暴力找路径，复杂度 $\Theta(nq)$。

$50$ pts

求路径上的最小值。对于询问 $(x,y,k)$，倍增求 LCA，在倍增的过程中同时维护路径上的最小值即可。

$70$ pts

同上，多维护一个次小值即可。

$100$ pts

用上述做法推广。对于询问 $(x,y,k)$，倍增求 LCA，答案是 $x,y$ 到路径上的第 $1,2,\dots,10$ 小值中的第 $k$ 小。时间复杂度 $\Theta(q \log^2 n)$。

T3-回忆

共有 $n$ 种记忆碎片，第一次选择若干种记忆碎片，第二次再在这若干种记忆碎片中选出不超过 $m$ 种记忆碎片。要求每次选择至少一种记忆碎片。求不同的方案数对 $10^9+7$ 取模的结果（定义不同的方案为任意一种选择不同的两种方案）。$n\le 10^9,m\le 5\times 10^6$。

不难发现题目是让我们求 $\sum\limits_{i=1}^n \sum\limits_{j=1}^m \binom{n}{i} \binom{i}{j}$。利用三项式恒等式转化为 $\sum\limits_{i=1}^n \sum\limits_{j=1}^m \binom{n}{j} \binom{n-j}{i-j}$。再利用二项式定理，此处我们可以让 $a,b$ 都等于 $1$，$\times 1$ 对答案无影响，最终化简为 $\sum\limits_{i=1}^m \binom{n}{i} 2^{n-i}$。

对于 $\binom{n}{i}$ 的计算，我们先上下约分，然后维护分子和分母，可以做到 $\Theta(m)$ 的预处理。

T4-到达层数【P3403 跳楼机】

直接把我赛时注释写的思路贴上吧。

不难发现可以到达的楼层是一个循环节，只需求出一个区间内的答案即可。

发现 $x,y,z$ 的范围不大，以此下手。以 $x$ 为例，我们求出 $\mod x = [0,x-1]$ 内的所有答案，最后统计个数。

因为我们要求 $x$，所以我们就只能通过 $y,z$ 来走到 $x$。

存在两种边的情况：$i+y->(i+y)\mod x,(i+z)->(i+z)\mod x$。

不难发现是最短路[因为答案为 $(h-dist_i)/x+1$，所以 $dist_i$ 越小越好，故最短路] 。

点击查看代码

int h,x,y,z;
std::vector<std::pair<int,int> >vec[MAXN]; 
void add(int u,int v,int d){
	vec[u].push_back(std::make_pair(v,d));
}

bool done[MAXN];
std::priority_queue<std::pair<int,int> > q;
int dist[MAXN];
void Dijkstra(){
	dist[0]=0;
	q.push(std::make_pair(0,0));
	while(q.size()){
		int u=q.top().second;
		q.pop();
		if(done[u])continue;
		done[u]=1;
		
		for(int i=0;i<vec[u].size();i++){
			int v=vec[u][i].first,d=vec[u][i].second;
			
			if(dist[v]>dist[u]+d){
				dist[v]=dist[u]+d;
				q.push(std::make_pair(-dist[v],v));
			}
		}
	}
}

signed main(){
	h=read(),x=read(),y=read(),z=read();
	h--;
	for(int i=0;i<x;i++){
		add(i,(i+y)%x,y);
		add(i,(i+z)%x,z);
		dist[i]=inf;
	}
	
	Dijkstra();
	int ans=0;
	for(int i=0;i<x;i++)
		if(h>=dist[i])ans+=(h-dist[i])/x+1;
	println(ans);
	return 0;
}

线段树进阶

权值线段树

维护的是一个值域。

e.g. 我们要维护 $[1,5,4,6,7,3,8,4,5,6]$ 中一段值域中数字出现的次数。相当于建桶，用线段树维护。根节点维护值域 $[1,8]$，左儿子维护值域 $[1,4]$，右儿子维护值域 $[5,8]$，以此类推。插入一个节点时，将其对应的叶子节点 $+1$，并不断向上给其祖先也 $+1$。可以用来查询值域在 $[l,r]$ 内的区间个数。

询问目前出现第 $k$ 小的数字。从根节点出发，若左儿子的值 $> k$，递归访问左儿子，反之则访问右儿子（当访问右儿子时，递归时 $k$ 的值应该减去左儿子的值），最后一定会递归到一个叶子节点。

当值域非常大时，我们可以离散化。

或者可以动态开点（详见下）。

动态开点

最初的时候不建树，只建根节点，代表整个区间。当要访问某一棵子树（子区间）时，再建立代表该子区间的节点（一直建立到叶子节点，并注意更新维护，其祖先及自己 $+1$）。

进行 $m$ 次单点操作后，值域/长度为 $w$ 的动态开点线段树的空间最多为 $O(m\log w)$。

节点编号并不是普通线段数的编号，而是按照建立出来的顺序给予编号，需要单独记录左右儿子（此种操作可以便于查看左右儿子是否建出）。

点击查看代码

int build(){
	cnt++;
	Tr[cnt].ls=Tr[cnt].rs=Tr[cnt].dat=0;
}

void update(int p,int l,int r,int val,int d){//单调修改（单点加 d，维护区间最值），val 基础上加 d
	if(l==r){
		Tr[p].dat+=d;
		return;
	} 
	
	int mid=(l+r)>>1;
	if(val<=mid){
		if(!Tr[p].ls)Tr[p].ls=build();
		update(Tr[p].ls,l,mid,val,d);
	}else{
		if(!Tr[p].rs)Tr[p].rs=build();
		update(Tr[p].rs,mid+1,r,val,d);
	}
	
	Tr[p].dat=std::max(Tr[Tr[p].ls].dat,Tr[Tr[p].rs].dat);
}

P1908 逆序对

动态开点权值线段树。不断插入一个数 $i$，当递归到左儿子时，答案加上右儿子的值（早出现，值比 $i$ 大）。

CF69E Subsegments

简化题意：对于长度为 $n$ 的数列，求每一个长度为 $k$ 的子区间内未重复出现过的数的最大值。

此题可以用 set 和离散化过掉，但我们考虑权值线段树。

对于一个节点，我们维护一个 $flag$，表示其子树内是否有出现过一次的数值。那么从根节点递归，若右儿子存在只出现过一次的数，那就递归访问右儿子，否则递归访问左儿子。

P3369 【模板】普通平衡树

动态开点权值线段树。

对应权值节点位置 $+1$。
对应权值节点位置 $-1$。
查询值域左边界到 $x-1$ 的数的数量。
同上，查第 $k$ 小。
值域左边界到 $x-1$ 的最大值。
$x+1$ 到值域右边界的最小值。

CF1042D Petya and Array

转化为前缀和，满足条件的区间为 $s_r-s_{l-1}>t$ 的区间 $[l,r]$，转化一下，$s_{l-1}>s_r-t$。

CF474E Pillars

首先考虑 DP。设 $f_i$ 表示以 $a_i$ 为结尾的子序列的长度，转移为 $f_i=\max\limits_{j<i,|a_i-a_j|\ge d} \left\{f_j\right\}+1$。

$pre_i$ 表示 $f_i$ 从 $f_{pre_i}$　转移而来，用于输出答案。

时间复杂度 $\Theta(n^2)$，不可接受，考虑如何更快地计算 $f_i$ 来优化。

建权值线段树，将 $f_j$ 的值给到 $a_j$ 的叶子上，维护区间最大值。在区间 $[a_i-d,a_i+d]$ 范围内查找区间最大值（就是我们要找的 $f_j$）。然后再将 $f_i$ 插入到 $a_i$ 位置的叶子上。

注意动态开点。

线段树合并

有若干棵线段树，都维护相同的值域 $[1,n]$，因此在线段树上的每个子区间的划分都是一致的。有 $m$ 次操作，操作在不同的线段树上。操作完成后，把对应的位置相加，同时维护区间最大值。

考虑如何合并两棵线段树。$p,q$ 分别指向两棵树的根节点，永远保持相同的区间。如果是动态开点，若都存在则将 $q$ 的值存到 $p$ 上并继续递归，如果有一个不存在就只记录存在的那个。

P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并

暴力，对于 $x$ 号点，记 $c_{x,j}$ 表示 $x$ 节点第 $j$ 种物品的数量。对于操作 $(x,y,z)$，遍历 $x->y$ 的路径，让路径上的点 $i$，$c_{i,z}++$。

树上差分可以优化复杂度，但他只适于解决一种物品的情况，此题有多种物品。

P3521 [POI2011] ROT-Tree Rotations

CF208E Blood Cousins

可持久化数据结构

可持久化 Trie 树

训练赛 #3

T1-aria 的礼物

求将一个长度为 $n$ 的小写字母构成的字符串变为前 $k$ 个字符和后 $k$ 个字符相同所需要改变的最少的字符的数量。

分类讨论 $k$ 的大小。

当 $k\le n/2$ 时，直接判断前 $k$ 位与后 $k$ 位有几位不同即可；

当 $k>n/2$ 时，对于每一个位置，每隔 $n-k$ 个位置的字母应该都是一样的，我们统计字母的数量 $sum$ 和出现次数最多的字母的数量 $maxn$，则对答案的贡献为 $sum-maxn$，注意标记。

注意特判 $n=k$ 的情况。时间复杂度 $\Theta(26n)$。

T2-神奇位运算

给定 $n$ 个长度为 $m$ 的 $01$ 串。有一台机器，可以输出一个长度同样为 $m$ 的 $01$ 字符串。对于每一位，机器可能对两个数位进行 $and,or,xor$ 其中一个操作。你可以随意选择两个数并无限次使用该机器，求最小要加上多少个 $01$ 串才能求出机器每一位的结果。

每一位都是独立的，我们分别考虑。

如果要区分 $and$ 和 $or$，需要 $0$ 和 $1$；如果要区分 $and$ 和 $xor$，需要 $0$ 和 $1$；如果要区分 $or$ 和 $xor$，需要 $1$ 和 $1$。所以每一位至少需要 $1$ 个 $0$ 和 $2$ 个 $1$，统计一下各位缺少的最大值即可。

T3-终焉之数列

给定数列 $a$，求数列 $b$，满足 $\gcd\limits_{1\le i<j \le n} (a_i,a_j)=1$，求 $\sum\limits_{i=1}^n |a_i-b_i|$ 的最小值。

状压 DP。设 $f_{i,sta}$ 表示在 $b$ 中前 $i$ 个数中，出现过的因子状态为 $sta$ 的最小绝对值总和。

首先我们发现最多使用 $16$ 个因子 $2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53$。原因是如果要用到 $\le 59$ 的数，不如把数字变成 $1$，代价永远不亏。

转移的时候枚举最后一位数 $b_i$，设 $b_i$ 的分解因子状态为 $div_{b_i}$，则我们可以枚举该位可以选什么数，得到转移方程 $f_{i,sta}=\min\limits_{b[i]=1}^{58} {sta\oplus div_{b_i} + |a_i-b_i|}$。

训练赛 #4

T1-变化的矩阵【CF1303F Number of Components】

给定 $n\times m$ 的矩阵，初始值均为 $0$。如果矩阵中的两个元素相邻且相等则其为相连的。

给出 $q$ 个形为 $x_i,y_i,c_i$ 的查询，对于每个查询进行以下操作：将元素 $a_{x_i,y_i}$ 替换为 $c_i$ 并计算矩阵中连通块的数量。

特别的，有 $1\le c_i\le c_{i+1}$。

令 $maxn=\max\left\{c_i|1\le i\le q\right\}$。将整个矩阵拆分成 $maxn$ 个矩阵，其中第 $i$ 个矩阵中只有权值是 $i$ 的元素。注意到 $maxn$ 个矩阵之间是相互独立的，所以我们要求的连通块总个数 $= maxn$ 个矩阵中连通块个数之和。

对于一次修改操作，将 $a_{x,y}$ 从 $c_1$ 修改到 $c_2$，相当于从 $c_2$ 个矩阵里多了一个点 $(x,y)$，在第 $c_1$ 个矩阵中少了一个点　$(x,y)$。

注意到多一个点可能会导致连通块个数减少，少一个点可能会导致连通块个数增加。因此每次操作对连通块个数的影响是第 $c_1$ 个矩阵中增加的连通块 $-$ 第 $c_2$ 个矩阵中减少的连通块。

先将所有操作读入。加点减少的连通块可以通过并查集来计算；删点增加的连通块也是经典问题，将所有操作倒序用并查集来计算。

总时间复杂度 $\Theta(maxn\times nm\log(nm))$。

点击查看代码

int n,m,q;
int maxn,ans[MAXQ],fa[MAXN*MAXN],now[MAXN][MAXN];

struct node{
	int id,x,y;
};
std::vector<node> vec1[MAXQ],vec2[MAXQ];

int dx[]={0,0,1,-1};
int dy[]={1,-1,0,0};

int get_fa(int x){
	return (x==fa[x]?x:fa[x]=get_fa(fa[x]));
}
bool merge(int x,int y){
	int fx=get_fa(x);
	int fy=get_fa(y);
	
	if(fx!=fy){
		fa[fx]=fy;
		return true;
	}
	
	return false;
}

int get_num(int x,int y){
	return (x-1)*m+y;
}

bool check(int x,int y){
	return (x>0&&x<=n&&y>0&&y<=m);
}

signed main(){
	n=read(),m=read(),q=read();
	for(int i=1;i<=q;i++){
		int x=read(),y=read(),c=read();
		node a;
		a.id=i,a.x=x,a.y=y;
		
		vec2[now[x][y]].push_back(a);
		now[x][y]=c;
		vec1[now[x][y]].push_back(a);
		
		maxn=c;
	}

	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++){
			node a;
			a.id=0,a.x=i,a.y=j;
			vec2[now[i][j]].push_back(a);
		}

    memset(now,-1,sizeof(now));
	
	for(int i=0;i<=maxn;i++){
		int siz=vec1[i].size();
		if(siz==0)continue;
		
		for(int i=1;i<=n*m;i++)
			fa[i]=i;
			
		for(int j=0;j<siz;j++){
			int nowid=vec1[i][j].id;
			int nowx=vec1[i][j].x;
			int nowy=vec1[i][j].y;
			
			ans[nowid]++;
			now[nowx][nowy]=i;
			
			for(int k=0;k<4;k++){
				int _x=nowx+dx[k];
				int _y=nowy+dy[k];
				
				if(check(_x,_y)&&now[_x][_y]==i&&merge(get_num(nowx,nowy),get_num(_x,_y)))
					ans[nowid]--;
			}
		}
	}

	memset(now,-1,sizeof(now));
	
	for(int i=0;i<=maxn;i++){
		int siz=vec2[i].size();
		if(siz==0)continue;
		
		for(int i=1;i<=n*m;i++)
			fa[i]=i;
			
		for(int j=siz-1;j>=0;j--){
			int nowid=vec2[i][j].id;
			int nowx=vec2[i][j].x;
			int nowy=vec2[i][j].y;
			
			ans[nowid]--;
			now[nowx][nowy]=i;
			
			for(int k=0;k<4;k++){
				int _x=nowx+dx[k];
				int _y=nowy+dy[k];
				
				if(check(_x,_y)&&now[_x][_y]==i&&merge(get_num(nowx,nowy),get_num(_x,_y)))
					ans[nowid]++;
			}
		}
	}

	ans[0]=1;
	for(int i=1;i<=q;i++){
		ans[i]+=ans[i-1];
		println(ans[i]);
	}
	
	return 0;
}

T2-树上三角

给出一棵 $n$ 个节点的树，树上相邻两点的距离均为 $1$，求满足以下条件的三元点集的个数：假设点集中有节点 $a,b,c$，则以 $dis(a,b),dis(a,c),dis(b,c)$ 为三边长的三角形存在。其中 $dis(a,b)$ 表示节点 $a$ 和 $b$ 在树上的距离。

考虑容斥，根据三角形三边长关系和三角不等式可以得到，当且仅当三点共链时无法构成三角形。

问题变成了求三点共线的点对的数量，枚举中点，计算子树贡献。

分讨，枚举 $x$ 的儿子 $v$，对答案贡献为 $v$ 子树内的数量 $\times$ $x$ 子树外节点数量。此时，当链的两端一端在 $x$ 子树内一端在子树外时的情况出现一次，而两端都在 $x$ 子树内的情况会出现两次（左右端点颠倒），所以我们在枚举完 $x$ 的节点后，要再加上一次第一种情况，最后将答案 $/2$。

点击查看代码

int n,ans,siz[MAXN];
std::vector<int> vec[MAXN];

void add(int u,int v){
	vec[u].push_back(v);
	vec[v].push_back(u);
}

void dfs(int x,int fa){
	siz[x]=1;
	for(int i=0;i<vec[x].size();i++){
		int v=vec[x][i];
		if(v==fa)continue;
		dfs(v,x);
		ans+=siz[v]*(n-1-siz[v]);
		siz[x]+=siz[v];
	}
	ans+=(siz[x]-1)*(n-siz[x]);
	return ;
}

signed main(){

	n=read();
	for(int i=1;i<n;i++){
		int x=read(),y=read();
		add(x,y);
	}
	
	dfs(1,0);
	
	int sum=n*(n-1)/2*(n-2)/3;
	println(sum-ans/2);

	return 0;
}

T3-喷泉【P7167 [eJOI2020 Day1] Fountain】

首先用单调栈维护每个圆盘往下第一个比自己大的节点的编号，考虑进一步计算的优化。首先根据单调性不难想到二分，但二分不好计算，容易想到倍增，倍增优化模拟可以将时间复杂度优化到 $\Theta((n+q)\log n)$。

点击查看代码

int n,q,c[MAXN],d[MAXN];
int nxt[MAXN][25],sum[MAXN][25];
std::stack<int> s;

void Stack(){
	for(int i=1;i<=n;i++){
		while(s.size()&&d[i]>d[s.top()]){
			nxt[s.top()][0]=i;
			sum[s.top()][0]=c[i];
			s.pop();
		}
		s.push(i);
	}
	
	while(s.size()){
		nxt[s.top()][0]=0;
		s.pop();
	}
	
	return;
} 

void Mul(){
	for(int j=1;j<=20;j++)
		for(int i=1;i<=n;i++){
			nxt[i][j]=nxt[nxt[i][j-1]][j-1];
			sum[i][j]=sum[i][j-1]+sum[nxt[i][j-1]][j-1];
		}
	return;
}

int query(int r,int v){
	if(c[r]>=v)return r;
	v-=c[r];
	for(int i=19;i>=0;i--)
		if(nxt[r][i]!=0&&v>sum[r][i]){
			v-=sum[r][i];
			r=nxt[r][i];
		}
	return nxt[r][0];
}

signed main(){
	n=read(),q=read(); 

	for(int i=1;i<=n;i++){
		d[i]=read();
		c[i]=read();
	}

	Stack();
	Mul();
	
	while(q--){
		int r=read(),v=read();
		println(query(r,v));
	}

	return 0;
}

图论

图的遍历

Problem 1

一张 $n$ 个点 $m$ 条边的图，每次连续走两步（中间的点不算被遍历到）可能遍历不完整个图，求至少加几条边才可以遍历完整张图。

首先，不同连通块之间必须连边。如果图中不存在奇环，需要构造奇环。找奇环用二分图染色的方法，构造奇环所需要加的边数为 $1$。

U468170 pull the box

给定一张无向图，$1$ 号点有一个箱子，你初始在点 $x$，你需要把箱子拉到 $n$ 号点，求最小步数或报告无解（不能走到箱子的点位上，和箱子相邻时才可以拉）。

整个过程分为人独自走和人拉着箱子走两个部分，注意不会出现拉上又放手的。

对于第一部分可以直接 BFS。第二部分也可以用有向边做 BFS，但是存在车轮图的情况，可能会被卡成 $\Theta(n^2)$。但是我们可以对走过的边标记，若一条边遍历 $> 2$ 次后就 continue 掉。

P5304 [GXOI/GZOI2019] 旅行者

对于 $k$ 个关键点将编号二进制分组，然后新建两个超级源点分别连接两个集合内的所有点，答案就是跑 $\log n$ 次两个超级源点之间的最短路后的最小值。

[ARC173D] Bracket Walk

首先，如果一个路径的左右括号数目相同，我们总是可以选择一个起点，使得这个路径是一个合法的括号序列。

题目没有限制路径的长度，我们可以找一个尽可能长的环经过每一个边且左右括号的数目相同。我们把左括号视为 $+1$，把右括号视为 $-1$，我们需要的就是找一个代数和为 $0$ 的环。

我们分讨图中的环的情况：

没有正环和负环

所有环的代数和为 $0$，我们可以任意拼接以来找到一个符合要求的路径。

只有正环/负环

无法均衡答案使得最终代数和为 $0$，显然不行。

既有正环又有负环

若两个正负环相邻，代数和分别为 $+x,-y$，我们可以从公共点出发，两个环分别绕 $y$ 和 $x$ 次使得代数和为 $0$。

若不相邻，我们可以走一些边走到另一个环上，然后再拐回来，就得到了挨着的两个环。于是我们显然可以找到一个环出发，然后走过所有的边再回来。然后与另外一个环结合一下即可得到所要求的路径。

CF575G Run for beer

反向 BFS，在步数一定的情况下最小化字典序，对于有前导零的情况，考虑从起点直接走到零的点而不经过其他点。

[ABC077D|ARC084B] Small Multiple

不难发现操作只存在 $\times 10$ 和 $+1$，$\times 10$ 时对答案无贡献，$+1$ 时会使答案 $+1$，所以我们可以使用同余最短路的思想用 $01 bfs$ 解决。

点击查看代码

int k;
bool vis[MAXN];
std::deque<std::pair<int,int> > q;

void bfs(){
	while(q.size()){
		std::pair<int,int> x=q.front();
		q.pop_front();
		if(vis[x.first])continue;
		vis[x.first]=1;
		
		if(x.first==0){
			println(x.second);
			exit(0);
		}
		
		q.push_front({(x.first*10)%k,x.second});
		q.push_back({(x.first+1)%k,x.second+1});
	}
	return ;
}

signed main(){

	k=read();
	q.push_back({1,1});
	bfs();
	 
	return 0;
}

CF1076D Edge Deletion

先删最短路树外的边，然后再不断地删叶子。

CF1163F Indecisive Taxi Fee

首先不考虑修改，考虑给出指定的边，求经过这条边的最短路。设边为 $(u,v)$，我们从 $1$ 和 $n$ 分别跑一次最短路，则最短长度为 $\min(dis_{1,u}+d_{u,v}+dis_{v,n},dis_{1,v}+d_{v,u}+dis_{u,n})$。

把修改分为以下几类：

修改的边在 $1$ 到 $n$ 的最短路上，边的长度变大了。
修改的边在 $1$ 到 $n$ 的最短路上，边的长度变小了。
修改的边不在 $1$ 到 $n$ 的最短路上，边的长度变大了。
修改的边不在 $1$ 到 $n$ 的最短路上，边的长度变小了。

对于 #$2$，答案为原最短路长度-原边长+新边长。
对于 #$3$，答案为原最短路长度。
对于 #$4$，答案为 $\min(dis_{1,u}+new_{u,v}+dis_{v,n},dis_{1,v}+new_{v,u}+dis_{u,n})$。
时间复杂度都是 $\Theta(1)$。

考虑计算 #$1$。考虑计算不经过 $(x,y)$ 的最短路。枚举不在路径上的所有边 $a,b$，找到两个端点到 $1$ 和 $n$ 的最短路径和 $1-n$ 的最短路径的交点 $L,R$。

对于 $L-R$ 内的每条边 $e$，不经过 $e$ 的路径的最小值和 $dis_{1,A}+dis_{B,n}+d_{A,B}$ 取 $\min$。这个操作可以用线段树来维护。

对于交点 $L,R$，我们可以在跑最短路的时候求出，也可以看成是在最短路的树上，$A$ 和 $n/B$ 和 $1$ 的 LCA。

P2505 [HAOI2012] 道路

首先考虑暴力做法，每次枚举起点和终点，统计每个点到起点的最短路数量，记作 $cnt1$，和每个点到终点的最短路数量，记作 $cnt2$，那么对边 $(u,v)$ 的贡献为 $cnt1_u\times cnt2_v$。

考虑优化，我们可以只枚举一个起点，构造最短路图，然后正着和反着各跑一次 DAG，类似于 P1144 最短路计数。

注意我们在跑最短路的时候已经跑出了最短路图上的正向 $DAG$，我们进行松弛操作的时候已经更新出 $cnt1$，所以最后只需要反着跑一遍 $DAG$ 来统计 $cnt2$ 即可。

点击查看代码

int n,m;
struct node{int nxt,val,num;};
std::vector<node> vec[MAXN];

int cnt1[MAXN],cnt2[MAXN],ans[MAXM],dis[MAXN];
bool vis[MAXN];

std::priority_queue<std::pair<int,int> > q;

void add(int u,int v,int w,int id){
	node a;
	a.nxt=v;
	a.val=w;
	a.num=id;
	
	vec[u].push_back(a);
	return ;
}

void Dijkstra(int s){
	memset(vis,0,sizeof(vis));
	memset(cnt1,0,sizeof(cnt1));
	memset(dis,0x7f,sizeof(dis));
	
	dis[s]=0;
	cnt1[s]=1;
	q.push({0,s});
	
	std::vector<int> now;
	while(q.size()){
		int u=q.top().second;
		q.pop();
		if(vis[u])continue;
		vis[u]=1;
		now.push_back(u);
		
		for(auto i:vec[u]){
			int v=i.nxt,w=i.val;
			
			if(dis[u]+w<dis[v]){
				dis[v]=dis[u]+w;
				cnt1[v]=cnt1[u];
				q.push({-dis[v],v});
			}else if(dis[u]+w==dis[v]){
				cnt1[v]+=cnt1[u];
			}
		}
	}
	
	std::reverse(now.begin(),now.end());
	
	for(auto u:now){//反着跑 DAG
		cnt2[u]=1;
		for(auto i:vec[u]){
			int v=i.nxt,w=i.val,num=i.num;
			if(dis[u]+w==dis[v]){
				cnt2[u]=(cnt2[u]+cnt2[v])%p;
				ans[num]=(ans[num]+(cnt1[u]*cnt2[v])%p)%p;
			}
		} 
	}
	
	return ;
}

signed main(){

	n=read(),m=read();
	for(int i=1;i<=m;i++){
		int u=read(),v=read(),w=read();
		add(u,v,w,i);
	}
	
	for(int i=1;i<=n;i++)Dijkstra(i);
	for(int i=1;i<=m;i++)println(ans[i]);

	return 0;
}

HDOJ7522 Cat 的最小生成树

[ABC355F] MST Query

注意到边权较小，可以建立 $10$ 个并查集，对于第 $i$ 个并查集存储所有权值 $x\le i$ 的边，并每次计算每一层的 Kruskal 同时得出当前这一层的连边情况，具体做法如下：

建立 $10$ 个并查集，设置答案的值为 $10(n-1)$，表示刚开始假设最小生成树的 $n-1$ 条边全部设置成最大值 $10$。
对于每一次操作，从当前这条边的权值所在的一层一直往上至第 $9$ 层并查集，每次对当前并查集进行加边操作。
每上一层答案 $-1$ 表示当前这条边多了 $1$ 的贡献。

[AGC016D] XOR Replace

设整个数列的异或和为 $x$，对 $a_i$ 进行操作相当于把 $a_i$ 变成 $x$，$x$ 变成 $x\oplus a_i\oplus x=a_i$，相当于交换 $a_i$ 和 $x$。

[AGC001F] Wide Swap

考虑原序列的逆排列，字典序拓扑原理，用线段树维护建图。

差分约束

P5980【模板】差分约束

板子，$a_x-a_y\le c$ 转化为 $a_x-c\le a_y$，从 $x$ 向 $y$ 连一条长度为 $c$ 的边，跑 SPFA。

P4926 [1007] 倍杀测量者

将倍数的运算转化为 $\log$ 式的加法不等式（$x\le ky=\log x\le \log(ky)=\log x\le \log k +\log y），跑差分约束。二分 $T$，对于每个 $T$ ，将 $x,y$ 之间连长度为 $k/T$ 的边，SPFA 判解。

P3275 [SCOI2011] 糖果

差分约束，边权只有 $0,1$，但 SPFA 会 T。只需判断是否会形成正环，拓扑即可，注意缩点。

P7515 [省选联考 2021 A 卷] 矩阵游戏

P2474 [SCOI2008] 天平

利用差值上下界差分约束，$n$ 较小，Floyd。

P3530 [POI2012] FES-Festival

图论生成树

LOJ #137. 最小瓶颈路（加强版）

给定 $n$ 个点 $m$ 条边的无向连通图，没有自环，可能有重边，每一条边有一个正权值 $w$。给出 $q$ 个询问，每次给出两个不同的点 $u,v$，求一条从 $u$ 到 $v$ 的路径上边权的最大值最小是多少，要求 $\Theta(1)$ 查询。

建出 Kruskal 重构树。首先建立 $n$ 个连通块，合并两个连通块时，找到二者的根，然后新开一个点（表示边），连接两个根，这个点成为新的根。然后两个点的 LCA 就表示这两个点的最小路径的最大值。

可以用欧拉序和 ST 表优化到每次 $\Theta(1)$ 查询 LCA。具体地，我们先求出 Kruskal 重构树的欧拉序（dfs 访问到的顺序），并记录下每个节点第一次出现的顺序，那么任意一对节点的 LCA 就是这两个点第一次出现的位置之间深度最小的点。

所以我们只需要对 $dfn$ 建立 ST 表，最后就可以 $\Theta(1)$ 查询区间最小值。

[AGC004D] Teleporter

保证从任何位置出发经过若干次传送过后都会到达 1 号点 保证一定是内向树。以 $1$ 为根，将 $1$ 的传送指向自己，深度 $> k$ 的点我们直接跳到 $1$ 号点并在上面循环 $k-1$ 次，深度 $<k$ 的同理也可以在 $1$ 号点上循环直到 $k$ 次。

[AGC002D] Stamp Rally

二分最大边权，建立 Kruskal 重构树，树上倍增即可。注意特判两点重合的情况。

P4768 [NOI2018] 归程

以海拔为第一关键字对边从大到小排序，建立 Kruskal 重构树，建立以海拔为关键字的小根堆。对于每棵子树，如果询问中的水位线低于子树的根节点，那么从这棵子树中的任意一点出发，可以开车到达子树中的其他所有点。

假设对于当前询问，找到了一个子树的根节点 $u$，满足 $d_u>p,d_{fa_u}\le p$ 且出发点 $v$ 在子树中，此时从 $v$ 出发可以到达子树中的任意一个叶子节点，所以我们只需要从众多叶子节点中选出一个距离 $1$ 号点花费最小的。

具体地，我们用 Dijkstra 最短路预处理每个点到 $1$ 号点的最小花费。然后建出 Kruskal 重构树，并用 DFS 维护以每个点为根节点时子树中距离 $1$ 号点的最小花费。最后加上点权 $> p$ 的限制后在树上倍增即可。

强联通分量

B3609 [图论与代数结构 701] 强连通分量

点击查看代码

int n,m,dfn[MAXN],low[MAXN],vis[MAXN],st[MAXN],top;
std::vector<int> vec[MAXN],ans[MAXN];
int cnt,num;
int Belong[MAXN],Print[MAXN];

void add(int u,int v){
	vec[u].push_back(v);
}

void Tarjan(int x){
	dfn[x]=low[x]=++cnt;
	vis[x]=1;
	st[++top]=x;
	
	for(auto y:vec[x]){
		if(!dfn[y]){
			Tarjan(y);
			low[x]=std::min(low[x],low[y]);
		}else if(vis[y]){
			low[x]=std::min(low[x],dfn[y]);
		}
	}
	
	if(dfn[x]==low[x]){
		int y=0;
		num++;
		do{
			vis[y=st[top--]]=0;
			ans[num].push_back(y);
			Belong[y]=num;
		}while(x^y);
	}
	
	return;
}

signed main(){

	n=read(),m=read();
	for(int i=1;i<=m;i++){
		int u=read(),v=read();
		add(u,v);
	}
	
	for(int i=1;i<=n;i++)
		if(!dfn[i])Tarjan(i); 
	
	println(num);
	
	for(int i=1;i<=n;i++)
		if(!Print[i]){
			int x=Belong[i];
			std::sort(ans[x].begin(),ans[x].end());
			for(auto j:ans[x]){
				Print[j]=1;
				std::cout<<j<<' ';
			}
			std::cout<<endl;
		}

	return 0;
}

P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G

用 Tarjan 跑出强连通分量，如果有且只有一个出度为 $0$ 的强连通分量，则答案为该强连通分量的大小，否则没有答案。

P2272 [ZJOI2007] 最大半连通子图

类似于缩点板子，缩点后找 $siz$ 最大的链。

注意原图不一定是一个半连通子图，可能存在原图中存在两点走不到的情况。

CF1239D Catowice City

对于每个评委连向除自己的猫外的其他认识的猫，缩点，出度为 $0$ 的当作猫，但要注意特殊处理一下全是评委的情况。

注意不如直接令第一个缩点后的节点为评委，因为它没有出度，其他的均为猫。

[ARC092F] Two Faced Edges

我们考虑有向边 $(x,y)$ 的两个端点是否能在删除该边后到达对方。

若能互相到达，则反向边后，$x,y$ 仍能互相到达，答案不变。
若都不能到达对方，则原图和反向边后的图中两点都不能互相到达，答案不变。
若仅能 $x$ 到达 $y$，则反向后会将 $x,y$ 合并到同一个强连通分量里，答案变小。
若仅能 $y$ 到达 $x$，则反向后 $x,y$ 会在不同的强连通分量内，答案变大。

现在我们只需要求出每个点能否到达对方即可。

判断 $y$ 是否能到达 $x$ 时，删边不会造成影响，路径永远不会经过 $x$ 到 $y$ 的边，跑 $n$ 次搜索即可。

判断 $x$ 能否到达 $y$ 时，也就是判断 $(x,y)$ 是否是路径上的必经边。两遍 DFS，按照出边正着一次，反着一次。同时记录一个点 $z$ 是从哪个出边到达的。所以对于点 $y$，如果两次都是通过 $(x,y)$ 这条出边遍历到的，那么这条边就是必经边。

缩点

P3387 【模板】缩点

和强连通分量相似，当 $dfn_u=low_u$ 时，此时栈中的节点同属于一个环，我们遍历栈，把答案都统计到 $u$ 点上，进行缩点，并不断弹栈。

割点

HDOJ7495 造花（困难版）

从“菊花图没有长度大于 $2$ 的路径”下手。如果有长度大于 $3$ 的路径，我们必须从这几个数中（可能是 $3$ 个点的环也可能是 $4$ 个点的链）删除一个，然后暴力判断即可。

P3469 [POI2008] BLO-Blockade

对于非割点，显然去掉后只有自己和其他的 $n-1$ 个点形成 $2(n-1)$ 个有序对。

考虑割点，去掉后，图会形成若干个连通块，在 DFS 时求出每个连通块的大小（或者求出割点后再求），然后对 $(n-siz)\times siz$ 求和即可。

P3225 [HNOI2012] 矿场搭建

分讨，看一个图内是否存在割点。

如果不存在，则答案为 $2$（可能存在一个出口坍塌的情况），总方案数为 $\binom{n}{2}$。

如果存在割点，那么会被割点分成若干个连通块，对于一个连通块我们只需要设置一个出口（若出口坍塌，我们可以通过割点走向其他的出口），所以出口数量为被分开的连通块的个数，方案数为各个连通块大小的乘积。

P1173 [NOI2016] 网格

首先注意到答案 $\le 2$，分类讨论答案的取值。

当只剩下一个或两个相邻的跳蚤时，答案为 $-1$。

当原图有两个跳蚤不在一个 $4$ 连通块内时，答案为 $0$。我们将每个蛐蛐周围的 $8$ 个跳蚤全部拿出来，看每个蛐蛐 $4$ 连通块周围的跳蚤是不是都在一个连通块内。

对于剩余的情况，我们不能只拿出周围一圈的 $8$ 个跳蚤，还需要向外面扩一圈（即周围 $24$ 个跳蚤），那这些跳蚤求割点，那么答案为 $1$。否则答案为 $2$。

割边

P8436 【模板】边双连通分量

P2783 有机化学之神偶尔会做作弊

简化题意：给定 $n$ 个点 $m$ 条边的无向图，把图中所有的环变成一个点，求变化后某两个点之间有多少个点。

HDOJ2460 Network

HDOJ7334 Cactus Circuit

利用边双缩点，所有边的最小值就是最大的 $T$。对环缩点，我们对边排序，取 $\min(e_1+e_2,e_3)$（环可以删掉一个点）。

CF555E Case of Computer Network

CF786B Legary

P5025 [SNOI2017] 炸弹

P3588 [POI2015] PUS

P8867 [NOIP2022] 建造军营

首先求出割边，若两侧都有军营则割边必须看守。求出边双，将边双缩点，边双内部的点选不选都可以，我们考虑缩点后的树，对其进行 DP。

设 $f_x$ 表示 $x$ 子树内至少建一个军营的方案数，初始值为 $2^{tot_x}$，其中 $tot_x$ 表示这个边双内（缩点）的点数，更新时考虑子节点 $y$ 的子树内有无军营。

若有，$(x,y)$ 必选，贡献为 $f_y$。
若无，$y$ 子树内部加上 $(x,y)$ 这条边共有 $siz_y$ 条边，贡献为 $2^{siz_y}$。

最后还要减去一个点都不选的情况，即 $2^{siz_x-1}$。

得到转移式 $f_x=\left\{y\in son_x|tot_x\times(f_y+2^{siz_y})-2^{siz_x-1}\right\}$。

考虑统计答案。令 $x$ 子树外的点一个都不选，也不选 $x$ 与其父亲的连边（这条边会在其父亲处统计）。所以最终答案为 $\sum\limits_{i=1}^n f_i\times 2^{n-siz_x-[fa_x\not=0]}$。

P5058 [ZJOI2004] 嗅探器

以 $A$ 为根做 Tarjan，将判断语句改成 if(low[y]>=dfn[x]&&x!=A&&dfn[y]<=dfn[B]) 即可，其中 $A,B$ 是两个信息中心。

P8435 【模板】点双连通分量

圆方树，每个点对应一个圆点，每一个点双对应一个方点，方点连接该点双内的所有圆点，不同的方点通过割点分开。方点不超过 $n-1$ 个。

总而言之，点双我们只需要找出割点，然后割点周围的连通块（包括自身）属于一个点双，边双同理。

点击查看代码

int n,m;
int dfn[MAXN],low[MAXN],st[MAXN],top,cnt,Fang;
std::vector<int> vec[MAXN],ans[MAXN];

void add(int u,int v){
	vec[u].push_back(v);
	vec[v].push_back(u);
}

void Tarjan(int x){
	st[++top]=x;
	dfn[x]=low[x]=++cnt;
	
	for(int i=0;i<vec[x].size();i++){
		int y=vec[x][i];
		if(!dfn[y]){
			Tarjan(y);
			low[x]=std::min(low[x],low[y]);
			if(dfn[x]<=low[y]){
				int z;
				Fang++;
				do{
					z=st[top--];
					ans[Fang].push_back(z);
				}while(z^y);
				ans[Fang].push_back(x);
			}
		}else low[x]=std::min(low[x],dfn[y]); 
	}
	
	if(vec[x].size()==0){
		Fang++;
		ans[Fang].push_back(x);
	}
	return ;
}

signed main(){

	n=read(),m=read();
	for(int i=1;i<=m;i++){
		int u=read(),v=read();
		if(u!=v)add(u,v);
	}
	
	Fang=n;
	for(int i=1;i<=n;i++)
		if(!dfn[i])Tarjan(i);
		
	println(Fang-n);
	for(int i=n+1;i<=Fang;i++){
		std::cout<<ans[i].size()<<' ';
		for(auto y:ans[i])
			std::cout<<y<<' ';
		std::cout<<endl;
	}

	return 0;
}

P4320 道路相遇

建出圆方树后，维护 $tot_x$ 表示 $x$ 到根节点的圆点的数目，求出 LCA 后直接计算即可。

P4606 [SDOI2018] 战略游戏

建出圆方树，找到所有要查询的节点，找到包含这些点的最小树，那么这个树内部的圆点数目就是答案。

不能暴力找，会 TLE。我们把点按 DFS 排序，形成一个环，对相邻两点求树上路径圆点个数之和，最后将答案 $/2$ 即可。

SP2878 KNIGHTS - Knights of the Round Table

将不憎恨的骑士连边，表示其可以坐在相邻的位置。只需判断每个骑士是否在一个存在奇环的点双内部即可。

CF487E Tourists

P5236 【模板】静态仙人掌

建出圆方树，从 $1$ 号点开始 DFS，若从圆点遍历到方点，边权为 $0$，否则设为那个圆点到这个方点父亲的最短距离（实际是环上两个部分取 $\min$）。

考虑求 $(x,y)$ 之间的距离，如果两点 LCA 是圆点，在圆方树上的距离就是答案。如果是方点，则我们先跳到 LCA 方点的儿子（即在环上的两点），答案为 $x,y$ 到各自在环上对应的点的距离和环上两点之间的距离（两个方向上的距离取 $\min$）。

HDOJ 7316 Teyvat

中文题意：给你一个仙人掌，每次询问给你若干个点，求有多少个点对，满足他们之间的任意路径全都经过这些关键点。

P7025 [NWRRC2017] Grand Test

2-SAT

P4782 【模板】2-SAT

可以这样考虑，$!A\to B$ 和 $!B\to A$，我们建图连边，对每个位置 $i$ 的值开两个点 $0/1$，点编号分别为 $i,i+n$，分别表示取值为 $0/1$。若存在 $A$ 与 $!A$ 在一个强连通分量里，则不合法，缩点判断，最后取强连通分量小的那个即可。

点击查看代码

int n,m;
int dfn[MAXN],low[MAXN],vis[MAXN],st[MAXN],top,cnt,id[MAXN],num;

std::vector<int> vec[MAXN];
void add(int u,int v){
	vec[u].push_back(v);
}

void Tarjan(int x){
	vis[x]=1;
	st[++top]=x;
	dfn[x]=low[x]=++cnt;
	
	for(auto y:vec[x]){
		if(!dfn[y]){
			Tarjan(y);
			low[x]=std::min(low[x],low[y]);
		}else if(vis[y])low[x]=std::min(low[x],dfn[y]);
	}
	
	if(dfn[x]==low[x]){
		int y;
		num++;
		do{
			y=st[top--];
			vis[y]=0;
			id[y]=num;
		}while(x^y);
	}
	
	return ;
} 

signed main(){

	n=read(),m=read();
	while(m--){
		int i=read(),a=read(),j=read(),b=read();
		add(i+a*n,j+(!b)*n);
		add(j+b*n,i+(!a)*n);
	}
	
	for(int i=1;i<=n+n;i++)
		if(!dfn[i])Tarjan(i);
		
	for(int i=1;i<=n;i++)
		if(id[i]==id[n+i]){
			puts("IMPOSSIBLE");
			return 0;
		}
		
	puts("POSSIBLE");
	for(int i=1;i<=n;i++) 
		std::cout<<(id[i]<=id[n+i])<<' ';

	return 0;
}

P5782 [POI2001] 和平委员会

对于一对厌恶的委员 $(x,y)$，我们设 $x$ 属于甲党派，$y$ 属于乙党派，那么若选择了 $x$，那么一定要选乙中的另一个委员 $y'$，从 $x$ 向 $y'$ 连边。反之同理，从 $y$ 向 $x'$ 连边。跑 2-SAT 模板即可。

点击查看代码

int n,m;
int dfn[MAXN],low[MAXN],vis[MAXN],st[MAXN],top,cnt,id[MAXN],num;

int get(int x){
	if(x%2==0)return x-1;
	return x+1;
} 

std::vector<int> vec[MAXN];
void add(int u,int v){
	vec[u].push_back(v);
}

void Tarjan(int x){
	vis[x]=1;
	st[++top]=x;
	dfn[x]=low[x]=++cnt;
	
	for(auto y:vec[x]){
		if(!dfn[y]){
			Tarjan(y);
			low[x]=std::min(low[x],low[y]);
		}else if(vis[y])low[x]=std::min(low[x],dfn[y]);
	}
	
	if(dfn[x]==low[x]){
		int y;
		num++;
		do{
			y=st[top--];
			vis[y]=0;
			id[y]=num;
		}while(x^y);
	}
	
	return ;
} 
signed main(){

	n=read(),m=read();
	while(m--){
		int a=read(),b=read();
		add(a,get(b));
		add(b,get(a));
	}
	
	for(int i=1;i<=n+n;i++)
		if(!dfn[i])Tarjan(i);
		
	for(int i=1;i<=n*2;i+=2)
		if(id[i]==id[1+i]){
			puts("NIE");
			return 0;
		}
		
	for(int i=1;i<=2*n;i+=2){
		if(id[i]<id[i+1])std::cout<<i<<endl;
		else std::cout<<i+1<<endl;
	}

	return 0;
}

P4171 [JSOI2010] 满汉全席

对于每个材料 $i$ 拆成两个点，点 $i$ 表示满式做法，点 $i+n$ 表示汉式做法，每个评委的限制条件看成或的形式。

$m_i,m_j$，连边 $i+n\to j,j+n\to i$。
$m_i,h_j$，连边 $i+n\to j+n,j\to i$。
$h_i,h_j$，连边 $i\to j+n,j\to i+n$。
$h_i,m_j$，连边 $i\to j,j+n\to i+n$。

注意多测要清空！！！

点击查看代码

int n,m;
int dfn[MAXN],low[MAXN],vis[MAXN],st[MAXN],top,cnt,id[MAXN],num;

std::vector<int> vec[MAXN];
void add(int u,int v){
	vec[u].push_back(v);
}

void Tarjan(int x){
	vis[x]=1;
	st[++top]=x;
	dfn[x]=low[x]=++cnt;
	
	for(auto y:vec[x]){
		if(!dfn[y]){
			Tarjan(y);
			low[x]=std::min(low[x],low[y]);
		}else if(vis[y])low[x]=std::min(low[x],dfn[y]);
	}
	
	if(dfn[x]==low[x]){
		int y;
		num++;
		do{
			y=st[top--];
			vis[y]=0;
			id[y]=num;
		}while(x^y);
	}
	
	return ;
}

void init(){
	top=cnt=num=0;
	for(int i=1;i<=2*n;i++){
		vec[i].clear();
		dfn[i]=low[i]=vis[i]=st[i]=id[i]=0; 
	}
	return ;
}

signed main(){
	
	int T=read();
	while(T--){
		n=read(),m=read();
		init();
		while(m--){
			std::string s1,s2;
			std::cin>>s1>>s2;
			int u=0,v=0;
			char c1=s1[0],c2=s2[0];
			for(auto i:s1)if(i>='0'&&i<='9')u=u*10+i-'0'; 
			for(auto i:s2)if(i>='0'&&i<='9')v=v*10+i-'0';
			
			if(c1=='m'){
				if(c2=='m')add(u+n,v),add(v+n,u);
				else add(u+n,v+n),add(v,u);
			}else{
				if(c2=='m')add(u,v),add(v+n,u+n);
				else add(u,v+n),add(v,u+n);
			}
		}
		
		for(int i=1;i<=n+n;i++)
			if(!dfn[i])Tarjan(i);
		
		bool f=1;
		for(int i=1;i<=n;i++)
			if(id[i]==id[n+i]){
				puts("BAD");
				f=0;
				break;
			}
			
		if(f)puts("GOOD");
	}

	return 0;
}

HDOJ 7308 Operation Hope

二分极差，考虑若 $i$ 同意了方案，那么 $j$ 是否该同意。如果 $i$ 同意了，$j$ 不同意会使得极差 $> mid$，那么 $i$ 同意指向 $j$ 同意，$j$ 不同意指向 $i$ 不同意，暴力建边会挂，考虑优化。

考虑把一个参数排序，那么 $i$ 同不同意影响的一定是一个前后缀，然后线段树优化建图即可。

注意可能存在 $i$ 同意使得无解的情况，此时我们需要强制 $i$ 不同意。

欢迎莅临本蒟蒻的博客~

摸底测试 #1

T1-咕咕

T2-找子串

CF148E

CF95E

摸底测试 #2

T1-江桥的均衡区间【P1360 [USACO07MAR] Gold Balanced Lineup G】

T2-江桥洗衣服【P1561 [USACO12JAN] Mountain Climbing S】

T3-江桥的三角形围栏【P1715 [USACO16DEC] Lots of Triangles P】

摸底测试 #3

T1-二元组序列

T2-攻打恶魔之巅

T3-牛牛的灯笼

基础算法杂题选讲

贪心

倍增与分治

构造

CFgym105214K

杂题

树上问题

树的直径

LCA

dfs 序

概念

DP

树上 DP

区间 DP

背包 DP

状压 DP

线头 DP

DP 杂题

训练赛 #1

T1-三角形的面积

T2-完全背包问题

T3-子集询问

T4-寻找宝藏

组合数学及计数

组合数学

计数技巧

水题 \(19\) 道选讲

训练赛 #2

T1-剑的比试【[ABC297D] Count Subtractions】

T2-顽皮的猴子【CF587C Duff in the Army】

T3-回忆

T4-到达层数【P3403 跳楼机】

线段树进阶

权值线段树

动态开点

线段树合并

可持久化数据结构

可持久化 Trie 树

训练赛 #3

T1-aria 的礼物

T2-神奇位运算

T3-终焉之数列

训练赛 #4

T1-变化的矩阵【CF1303F Number of Components】

T2-树上三角

T3-喷泉【P7167 [eJOI2020 Day1] Fountain】

图论

图的遍历

Problem 1

HDOJ7522 Cat 的最小生成树

差分约束

图论生成树

强联通分量

缩点

割点

HDOJ7495 造花（困难版）

割边