从2-3树到 红黑树
清晰理解红黑树的演变---红黑的含义
前言
红黑树,对不少人来说是个比较头疼的名字,在网上搜资料也很少有讲清楚其演变来源的,多数一上来就给你来五条定义,红啊黑啊与根节点距离相等之类的,然后就开始进行旋转、插入、删除这些操作。一通操作下来,连红色和黑色怎么来的,是什么含义,有什么作用都云里雾里的,能搞清楚就怪了。
本文介绍红黑树,暂时不涉及任何代码,只是帮助你理解红黑树的演变来源,树结构中红黑色具体含义,保证你理解了过后,再去看什么旋转插入的东西,要清晰得多。换句话说,理解本文要描述的内容是从代码级理解红黑树的基础。
开始之前,我还是恳请你保持耐心,一步一步仔细看完,浮躁的话真的做不好任何事情。
正文
红黑树的起源,自然是二叉查找树了,这种树结构从根节点开始,左子节点小于它,右子节点大于它。每个节点都符合这个特性,所以易于查找,是一种很好的数据结构。但是它有一个问题,就是容易偏向某一侧,这样就像一个链表结构了,失去了树结构的优点,查找时间会变坏。
所以我们都希望树结构都是矮矮胖胖的,像这样:

而不是像这样:
在这种需求下,平衡树的概念就应运而生了。
红黑树就是一种平衡树,它可以保证二叉树基本符合矮矮胖胖的结构,但是理解红黑树之前,必须先了解另一种树,叫2-3树,红黑树背后的逻辑就是它。
好吧来看2-3树吧。
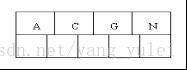
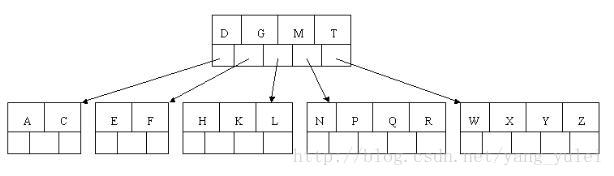
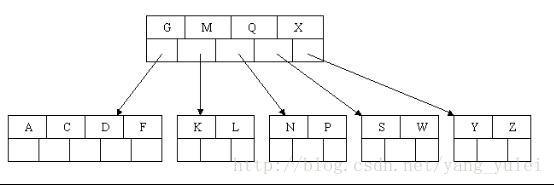
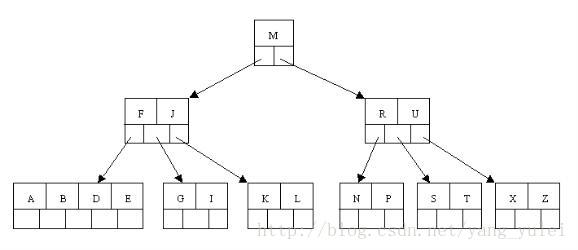
2-3树是二叉查找树的变种,树中的2和3代表两种节点,以下表示为2-节点和3-节点。
2-节点即普通节点:包含一个元素,两条子链接。
3-节点则是扩充版,包含2个元素和三条链接:两个元素A、B,左边的链接指向小于A的节点,中间的链接指向介于A、B值之间的节点,右边的链接指向大于B的节点。
2-节点: 3-节点:
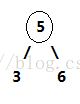
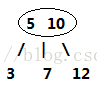
在这两种节点的配合下,2-3树可以保证在插入值过程中,任意叶子节点到根节点的距离都是相同的。完全实现了矮胖矮胖的目标。怎么配合的呢,下面来看2-3树的构造过程。
所谓构造,就是从零开始一个节点一个节点的插入。
在二叉查找树中,插入过程从根节点开始比较,小于节点值往右继续与左子节点比,大于则继续与右子节点比,直到某节点左或右子节点为空,把值插入进去。这样无法避免偏向问题。在2-3树中,插入的过程是这样的。
如果将值插入一个2-节点,则将2-节点扩充为一个3-节点。
如果将值插入一个3-节点,分为以下几种情况。
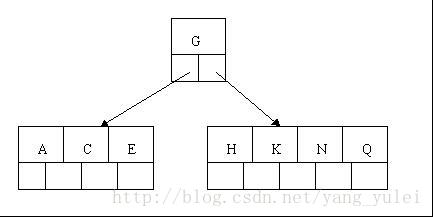
(1).3-节点没有父节点,即整棵树就只有它一个三节点。此时,将3-节点扩充为一个4-节点,即包含三个元素的节点,然后将其分解,变成一棵二叉树。

此时二叉树依然保持平衡。
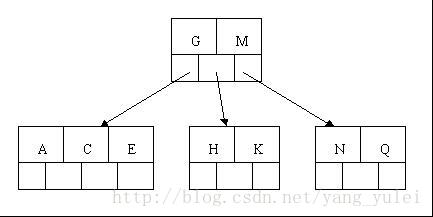
(2).3-节点有一个2-节点的父节点,此时的操作是,3-节点扩充为4-节点,然后分解4-节点,然后将分解后的新树的父节点融入到2-节点的父节点中去。

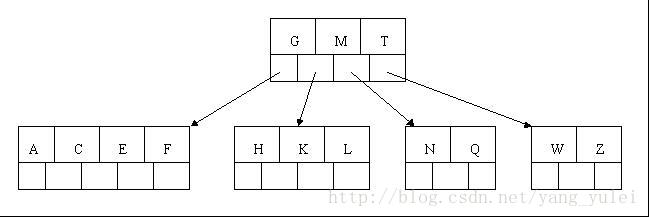
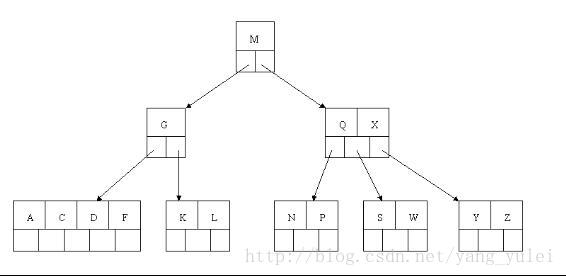
(3).3-节点有一个3-节点的父节点,此时操作是:3-节点扩充为4-节点,然后分解4-节点,新树父节点向上融合,上面的3-节点继续扩充,融合,分解,新树继续向上融合,直到父节点为2-节点为止,如果向上到根节点都是3-节点,将根节点扩充为4-节点,然后分解为新树,至此,整个树增加一层,仍然保持平衡。
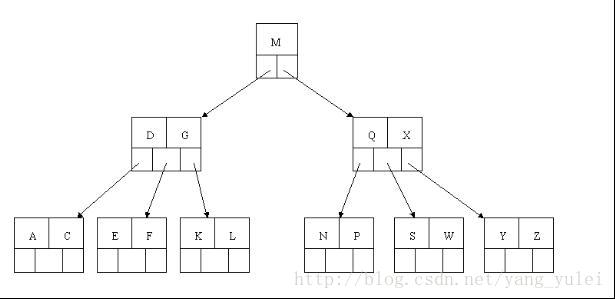
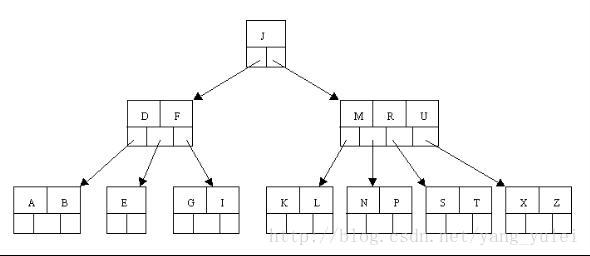
第三种情况稍微复杂点,为了便于直观理解,现在我们从零开始构建2-3树,囊括上面所有的情况,看完所以步骤后,你也可以自己画一画。
我们将{7,8,9,10,11,12}中的数值依次插入2-3树,画出它的过程:
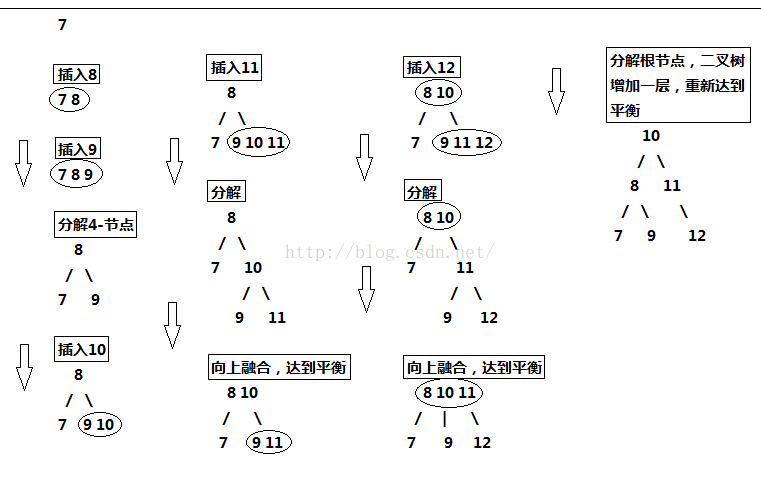
所以,2-3树的设计完全可以保证二叉树保持矮矮胖胖的状态,保持其性能良好。但是,将这种直白的表述写成代码实现起来并不方便,因为要处理的情况太多。这样需要维护两种不同类型的节点,将链接和其他信息从一个节点复制到另一个节点,将节点从一种类型转换为另一种类型等等。
因此,红黑树出现了,红黑树的背后逻辑就是2-3树的逻辑,但是由于用红黑作为标记这个小技巧,最后实现的代码量并不大。(但是,要直接理解这些代码是如何工作的以及背后的道理,就比较困难了。所以你一定要理解它的演化过程,才能真正的理解红黑树)
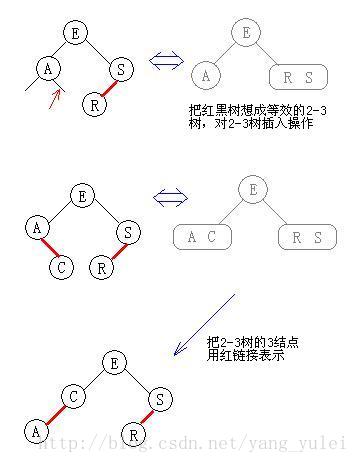
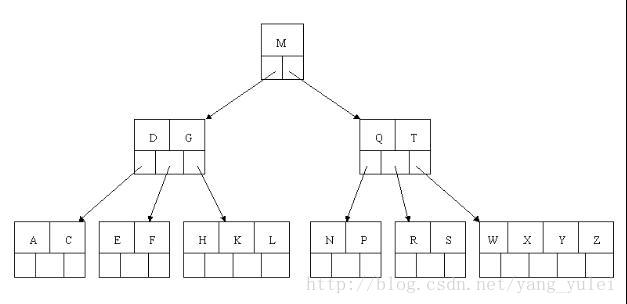
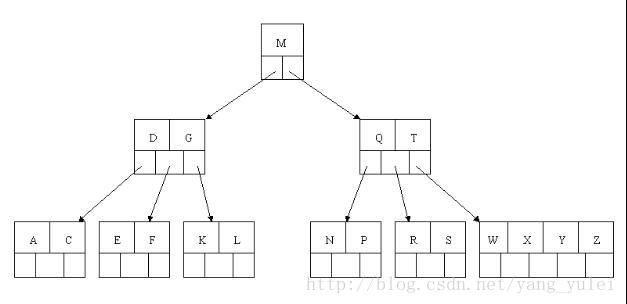
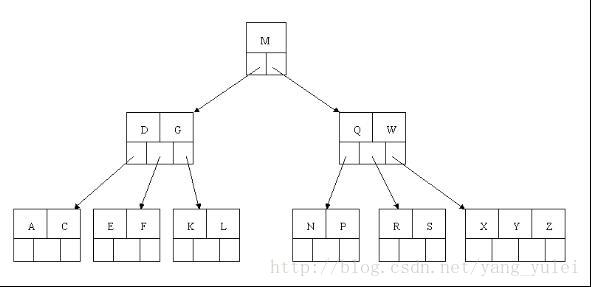
我们来看看红黑树和2-3树的关联,首先,最台面上的问题,红和黑的含义。红黑树中,所有的节点都是标准的2-节点,为了体现出3-节点,这里将3-节点的两个元素用左斜红色的链接连接起来,即连接了两个2-节点来表示一个3-节点。这里红色节点标记就代表指向其的链接是红链接,黑色标记的节点就是普通的节点。所以才会有那样一条定义,叫“从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点”,因为红色节点是可以与其父节点合并为一个3-节点的,红黑树实现的其实是一个完美的黑色平衡,如果你将红黑树中所有的红色链接放平,那么它所有的叶子节点到根节点的距离都是相同的。所以它并不是一个严格的平衡二叉树,但是它的综合性能已经很优秀了。
借一张别人的图来看:
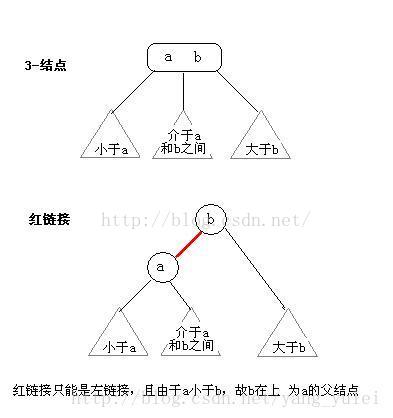
红链接放平:
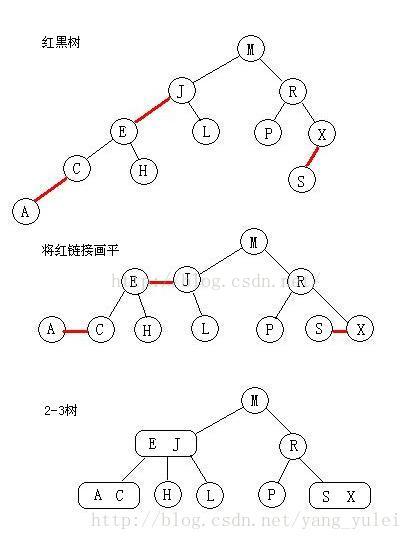
所以,红黑树的另一种定义是满足下列条件的二叉查找树:
⑴红链接均为左链接。
⑵没有任何一个结点同时和两条红链接相连。(这样会出现4-节点)
⑶该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑链接数量相同。
理解了这个过程以后,再去看红黑树的各种严格定义,以及其插入,删除还有旋转等操作,相信你脑子里的思路会清晰得多的。
TreeMap红黑树源码详解
尊重原创,转载请标明出处 http://blog.csdn.net/abcdef314159
在分析源代码之前,最好要标注出处,因为在Java中和Android中同一个类可能代码就会不一样,甚至在Android中不同版本之间代码也可能会有很大的差别,下面分析的是红黑树TreeMap,在\sources\android-25中。
红黑树的几个性质要先说一下,
1. 每个节点是红色或者黑色的。
2. 根节点是黑色的。
3. 每个叶节点的子节点是黑色的(叶子节点的子节点可以认为是null的)。
4. 如果一个节点是红色的,则它的左右子节点都必须是黑色的。
5. 对任意一个节点来说,从它到叶节点的所有路径必须包含相同数目的黑色节点。
TreeMap还有一个性质,就是他的左子树比他小,右子树比他大,这里的比较是按照key排序的。存放的时候如果key一样就把他替换了。

乍一看代码TreeMap有3000多行,其实他里面有很多内部类,有Values,EntrySet,KeySet,PrivateEntryIterator,EntryIterator,ValueIterator,KeyIterator,DescendingKeyIterator,
NavigableSubMap,AscendingSubMap,DescendingSubMap,SubMap,TreeMapEntry,TreeMapSpliterator,KeySpliterator,DescendingKeySpliterator,ValueSpliterator,
EntrySpliterator多达十几个内部类。其实很多都不需要了解,下面主要来看一下TreeMapEntry这个类,它主要是红黑树的节点
/**
* Node in the Tree. Doubles as a means to pass key-value pairs back to
* user (see Map.Entry).
*/
static final class TreeMapEntry<K,V> implements Map.Entry<K,V> {
K key;
V value;
TreeMapEntry<K,V> left = null;//左子树
TreeMapEntry<K,V> right = null;//右子树
TreeMapEntry<K,V> parent;//父节点
boolean color = BLACK;//默认为黑色
/**
* Make a new cell with given key, value, and parent, and with
* {@code null} child links, and BLACK color.
*/
TreeMapEntry(K key, V value, TreeMapEntry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
/**
* Returns the key.
*
* @return the key
*/
public K getKey() {
return key;
}
/**
* Returns the value associated with the key.
*
* @return the value associated with the key
*/
public V getValue() {
return value;
}
/**
* Replaces the value currently associated with the key with the given
* value.
*
* @return the value associated with the key before this method was
* called
*/
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
public String toString() {
return key + "=" + value;
}
}既然是棵树,那么肯定就会有put方法以及remove方法,那么这里就从最简单的着手,先看一下put方法
/**
* Associates the specified value with the specified key in this map.
* If the map previously contained a mapping for the key, the old
* value is replaced.
*
* @param key key with which the specified value is to be associated
* @param value value to be associated with the specified key
*
* @return the previous value associated with {@code key}, or
* {@code null} if there was no mapping for {@code key}.
* (A {@code null} return can also indicate that the map
* previously associated {@code null} with {@code key}.)
* @throws ClassCastException if the specified key cannot be compared
* with the keys currently in the map
* @throws NullPointerException if the specified key is null
* and this map uses natural ordering, or its comparator
* does not permit null keys
*/
//注释说的很明白,如果有相同的key,那么之前老的就会被代替,
public V put(K key, V value) {
TreeMapEntry<K,V> t = root;
if (t == null) {
// We could just call compare(key, key) for its side effect of checking the type and
// nullness of the input key. However, several applications seem to have written comparators
// that only expect to be called on elements that aren't equal to each other (after
// making assumptions about the domain of the map). Clearly, such comparators are bogus
// because get() would never work, but TreeSets are frequently used for sorting a set
// of distinct elements.
//
// As a temporary work around, we perform the null & instanceof checks by hand so that
// we can guarantee that elements are never compared against themselves.
//
// compare(key, key);
//
// **** THIS CHANGE WILL BE REVERTED IN A FUTURE ANDROID RELEASE ****
// key检查,如果comparator为null,那么key是不能为null的,并且key是实现Comparable接口的,因为TreeMaori是有序的,需要比较.
//如果comparator不为null,则需要验证,comparator是自己传进来的,根据key == null,comparator.compare(key, key)是否可执行,
//还是抛异常,这个是由你自己写的compare方法决定的。
if (comparator != null) {
if (key == null) {
comparator.compare(key, key);
}
} else {//如果没有传入comparator,则key不能为null,且必须实现Comparable接口
if (key == null) {
throw new NullPointerException("key == null");
} else if (!(key instanceof Comparable)) {
throw new ClassCastException(
"Cannot cast" + key.getClass().getName() + " to Comparable.");
}
}
//创建root,这个是在上面root为null的时候才走到这一步
root = new TreeMapEntry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
TreeMapEntry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
//comparator无论是等于null还是不等于null,原理都是基本差不多
if (cpr != null) {
do {//添加的时候如果原来有就替换,如果没有就不断的循环,这里注意TreeMap的左子树比他小,右子树比他大,这里比较的是key
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)//小的就找左子树
t = t.left;
else if (cmp > 0)//大的就找右子树
t = t.right;
else
return t.setValue(value);//如果正好找到了就把它替换掉
} while (t != null);
}
else {//这个是使用默认的比较器,原理和上面是一样的
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
TreeMapEntry<K,V> e = new TreeMapEntry<>(key, value, parent);//创建一个节点
if (cmp < 0)//节点比他父节点小,放到左子树
parent.left = e;
else
parent.right = e;//节点比他父节点大,放到右子树
fixAfterInsertion(e);
//这里是关键,树的调整,因为上面创建节点的时候默认的是一棵黑色的数,而树原来是平衡的,加入节点之后导致数的不平衡,所以需要调节
size++;
modCount++;
return null;
}put方法存放的时候,首先是会存放到叶子节点,然后在进行调整。上面有一个重量级的方法fixAfterInsertion还没有分析,在分析fixAfterInsertion方法之前来看一下其他的几个方法,
private static <K,V> boolean colorOf(TreeMapEntry<K,V> p) {
//获取树的颜色,如果为null,则为黑色,这一点要记住,待会下面分析的时候会用到
return (p == null ? BLACK : p.color);
}
//找父节点
private static <K,V> TreeMapEntry<K,V> parentOf(TreeMapEntry<K,V> p) {
return (p == null ? null: p.parent);
}
//设置节点颜色
private static <K,V> void setColor(TreeMapEntry<K,V> p, boolean c) {
if (p != null)
p.color = c;
}
//获取左子树
private static <K,V> TreeMapEntry<K,V> leftOf(TreeMapEntry<K,V> p) {
return (p == null) ? null: p.left;
}
//获取右子树
private static <K,V> TreeMapEntry<K,V> rightOf(TreeMapEntry<K,V> p) {
return (p == null) ? null: p.right;
}下面再来看一下fixAfterInsertion方法
/** From CLR */
private void fixAfterInsertion(TreeMapEntry<K,V> x) {
//在红黑树里面,如果加入一个黑色节点,则导致所有经过这个节点的路径黑色节点数量增加1,
//这样就肯定破坏了红黑树中到所有叶节点经过的黑色节点数量一样的约定。所以,
//我们最简单的办法是先设置加入的节点是红色的。
x.color = RED;
//当前节点变为红色,如果他的父节点是红色则需要调整,因为父节点和子节点不能同时为红色,但可以同时为黑色,
//所以这里的循环条件是父节点必须为红色才需要调整。
while (x != null && x != root && x.parent.color == RED) {
//这里会分多钟情况讨论,
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {//如果父节点是爷爷节点的左节点
TreeMapEntry<K,V> y = rightOf(parentOf(parentOf(x)));//当前节点的叔叔节点,也就是他父节点的兄弟节点,这个也可能为null
if (colorOf(y) == RED) {
//因为添加的是红色,而父与子不能同时为红色,所以打破了平衡,需要先让父为黑色,然后再让爷爷为红色,因为爷爷节点为红色,所以
//子节点必须为黑色,所以把叔叔节点也调为黑色,继续往上调整,
//(1)如果当前节点的叔叔节点是红色,也就是说他的叔叔节点一定是存在的,因为如果为null,则colorOf会返回黑色。既然叔叔节点
//是红色,那么他的爷爷节点一定是黑色,否则就打破了红黑平衡,那么他的父节点也一定是红色,因为只有父节点为红色才执行while
//循环,这种情况下,无论x是父节点的左节点还是右节点都不需要在旋转,
setColor(parentOf(x), BLACK);//让x的父节点为黑色
setColor(y, BLACK);//叔叔节点也设为黑色
setColor(parentOf(parentOf(x)), RED);//当前节点的爷爷节点为红色
//把爷爷节点设置为红色之后,继续往上循环,即使执行到最上端也不用担心,因为在最后会把根节点设置为黑色的。
x = parentOf(parentOf(x));
} else {
//如果他的叔叔节点是黑色的,并且他的父节点是红色的,那么说明他的叔叔节点是null,因为如果叔叔节点是黑色的且不为空,
//那么违反了他的第5条性质所以这里叔叔节点是空。因为叔叔节点
//为空,出现了不平衡,所以这里当前节点无论是父节点的左节点还是右节点,都需要旋转
if (x == rightOf(parentOf(x))) {
//(2)当前节点是父节点的右节点,
x = parentOf(x);//让当前节点的父节点为当前节点
rotateLeft(x);//对父节点进行左旋
}
//(3)当前节点是父节点的左节点,这个左节点有可能是添加的时候添加到左节点的,也有可能是上面旋转的时候旋转到左节点的
setColor(parentOf(x), BLACK);//让父节点为黑色
setColor(parentOf(parentOf(x)), RED);//爷爷节点变为红色
rotateRight(parentOf(parentOf(x)));//对爷爷节点右旋
}
} else {//父节点为爷爷节点的右节点
TreeMapEntry<K,V> y = leftOf(parentOf(parentOf(x)));//找出叔叔节点
//如果叔叔节点是红色,那么说明他一定是存在的,所以不需要旋转,这里要铭记,无论是左旋还是右旋的前提条件是他的叔叔节点不存在,
//如果存在就不需要旋转,只需要遍历改变颜色值即可
if (colorOf(y) == RED) {
//(4)修改颜色
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));//改变颜色之后遍历
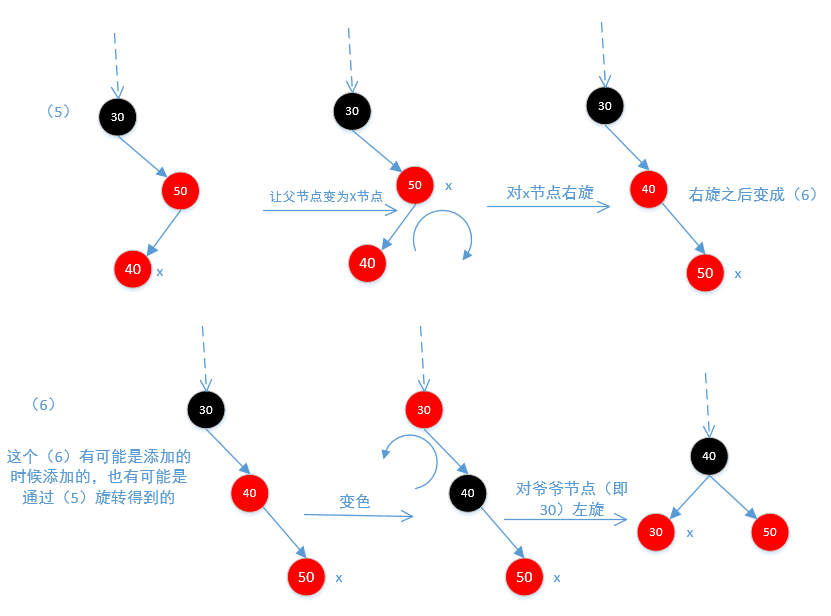
} else {//没有叔叔节点
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);//(5)右旋操作
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));//(6)左旋操作
}
}
}
root.color = BLACK;//根节点必须是黑色
}上面列出了6中可能,下面通过6张图来说明
下面是图1,不需要旋转,只需要调整颜色即可

下面是图2和图3,因为不平衡,所以需要旋转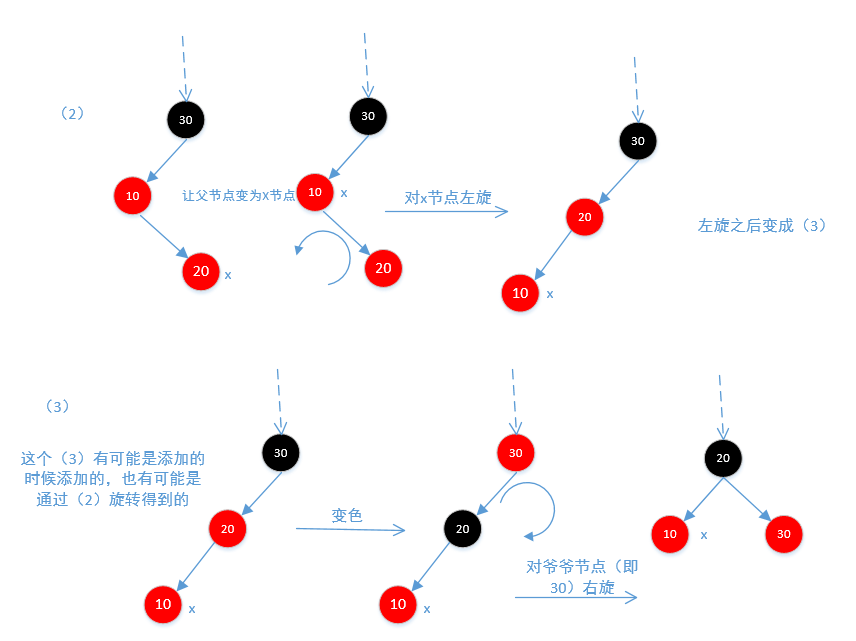
下面是图4,和图1差不多,也分两种情况,一种是左节点一种是右节点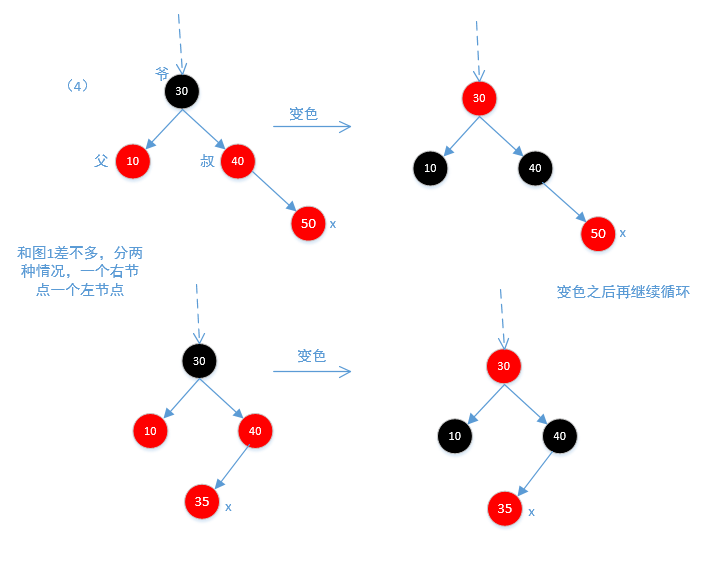
下面是图5和图6,因为不平衡,所以需要旋转
无论怎么旋转,他的左节点永远小于他,右节点永远大于他。通过不断的while循环,最终保证红黑树的平衡。下面来看一下旋转的方法,先看一下图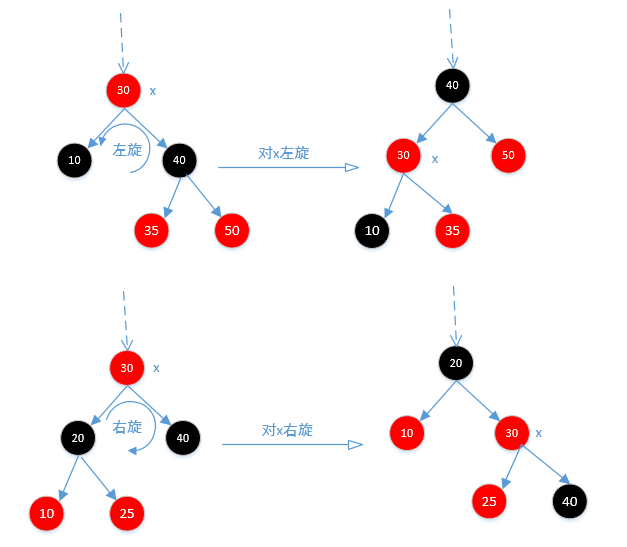
/** From CLR */
private void rotateLeft(TreeMapEntry<K,V> p) {
//参照上面旋转的图来分析,p就是图中的x
if (p != null) {
TreeMapEntry<K,V> r = p.right;//r相当于图中的40节点
p.right = r.left;//让35节点(r.left也就是图中40节点的左节点)等于p的右节点,看上图
//如果r.left!=null,让p等于他的父节点,因为在上一步他已经等于p的右节点,自然就是他的子节点
//所以他的父节点自然就变成p了
if (r.left != null)
r.left.parent = p;
//让原来p节点的父节点等于r的父节点,可以根据图看的很明白,通过旋转40节点,挪到上面了,
r.parent = p.parent;
//这里也很好理解,如果原来p的父节点为null,说明原来父节点就是根节点,这里让调整过来的r节点
//(即40节点)成为根节点
if (p.parent == null)
root = r;
//这里很好理解,如果原来p节点是左节点就让调整过来的r节点变成左节点,是右节点就让r变成右节点
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
//让p(也就是图中的30节点)成为r(也就是图中的40节点)的左节点,
r.left = p;
//然后让r(图中的40节点)成为p(图中的30节点)的父节点。
p.parent = r;
}
}而右旋方法rotateRight和左旋差不多,这里就不在分析。put方法分析完了,那么下一个就是remove方法了,
public V remove(Object key) {
//getEntry(Object key)方法是获取TreeMapEntry,如果比当前节点大则找右节点,如果比当前节点小则找左节点
//通过不断的循环,知道找到为止,如果没找着则返回为null。
TreeMapEntry<K,V> p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
//找到之后删除
deleteEntry(p);
return oldValue;
}下面再看一下删除方法deleteEntry。
/**
* Delete node p, and then rebalance the tree.
*/
private void deleteEntry(TreeMapEntry<K,V> p) {
modCount++;
size--;//删除,size减1
// If strictly internal, copy successor's element to p and then make p
// point to successor.
//当有两个节点的时候不能直接删除,要删除他的后继节点,后继节点最多只有一个子节点。因为如果p有两个子节点,你删除之后
//他的两个子节点怎么挂载,挂载到p的父节点下?这显然不合理,因为这样一来p的父节点很有可能会有3个子节点,那么最好的办法
//就是找一个替罪羊,删除p的后继节点s,当然删除前需要把后继节点s的值赋给p
if (p.left != null && p.right != null) {
//successor(p)返回p节点的后继节点,其实这个后继节点就是比p大的最小值,这个待会再分析
TreeMapEntry<K,V> s = successor(p);
//把后继节点s的值赋值给p,待会删除的是后继节点s,注意这里赋值并没有把颜色赋给原来的p。当然这里删除并不会打乱树的
//大小顺序,因为后继节点是比p大的最小值,赋值之后在删除,树的大小顺序依然是正确的,这里只是把s的值赋给了p,如果
//再把p原来的值赋给s,在删除s可能就会更好理解了,但这其实并不影响。
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
TreeMapEntry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
//p有子节点,并且有且只有一个节点,因为如果p有两个节点,那么上面的successor方法会一直查找,要么返回p的右节点
//(前提是p的右节点没有左节点),要么会一直循环找到p的右节点的最左孙子节点。待会看successor代码会发现,如果p
//有2个子节点,那么successor返回的节点最多也只有1个节点。
// Link replacement to parent
replacement.parent = p.parent;
//如果p的父节点为null,说明p是root节点,因为执行到这一步,所以replacement是p唯一的节点,把p节点删除后,让
//replacement成为root节点
if (p.parent == null)
root = replacement;
//这个不会变,原来p是左节点就让replacement成为左节点,原来p为右节点就让replacement成为右节点。相当于替换p节点的位置
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
//把p的子节点及父节点全部断开
p.left = p.right = p.parent = null;
// Fix replacement
//如果删除的是黑色要进行调整,因为黑色删除会打破红黑平衡,
//所以这里只是做颜色调整,调整的时候并没有删除。
if (p.color == BLACK)
//上面的p确定只有一个节点replacement,但这里replacement子节点是不确定的,有可能0个,1个或2个。
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
root = null;//p是根节点,直接删除,不用调整
} else { // No children. Use self as phantom replacement and unlink.
//p没有子节点,说明p是个叶子节点,不需要找继承者,调整完之后直接删除就可以了。
//如果删除的是黑色,需要调整,上面的调整是删除之后再调整,是因为删除的不是叶子节点,如果调整之后再删除还有可能出现错误,
//而这里是调整之后再删除,是因为这里删除的是叶子节点,调整完之后直接把叶子节点删除就是了,删除之后调整的是颜色,并不是树的
//大小顺序
if (p.color == BLACK)
fixAfterDeletion(p);
//调整完之后再删除p节点,此时p是叶子节点,因为调整完之后通过左旋或右旋p.rarent可能为null,所以这里需要判断
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}上面分析的时候有两个方法successor和fixAfterDeletion没有分析,下面先来看一下successor方法,这个方法很简单,其实就是返回大于节点p的最小值,看一下代码
/**
* Returns the successor of the specified Entry, or null if no such.
*/
static <K,V> TreeMapEntry<K,V> successor(TreeMapEntry<K,V> t) {
if (t == null)
return null;
else if (t.right != null) {//t的右节点不为空
TreeMapEntry<K,V> p = t.right;
//循环左节点,如果左节点一开始就为null,那么直接就返回p,此时p是t的右节点,如果p的左节点
//存在,那么会一直循环,一直在找左节点,直到为null为止,
while (p.left != null)
p = p.left;
return p;//所以查找到最后,返回的p最多只有一个节点,并且查找的p是大于t的最小值
} else {
TreeMapEntry<K,V> p = t.parent;
TreeMapEntry<K,V> ch = t;
//不停的往上找父节点,直到p为null,或者父节点(这个父节点也可能是父节点的父节点的父节点,反正
//只要满足条件就会一直往上循环)是左节点,最终查找的结果是p是大于t的最小值,要明白这一点,首先要
//明白,一个节点大于他的左节点小于他的右节点
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;//这里返回的p有可能有2个子节点,并且只有在t没有右节点的时候才有可能。
}
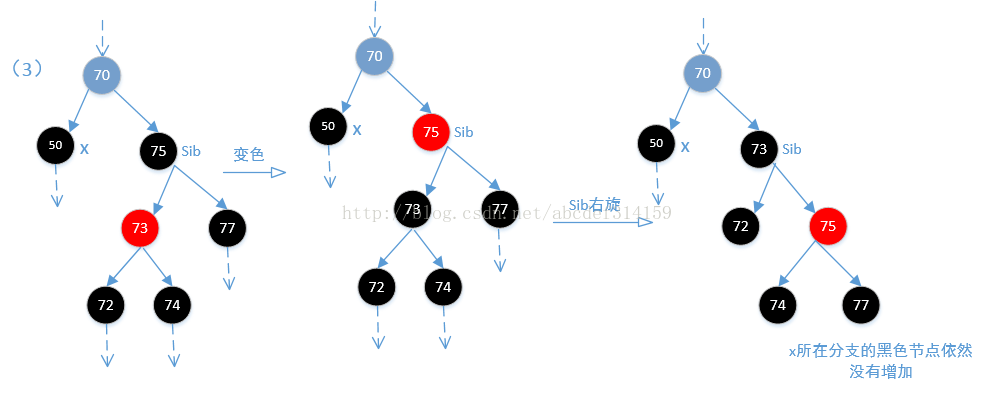
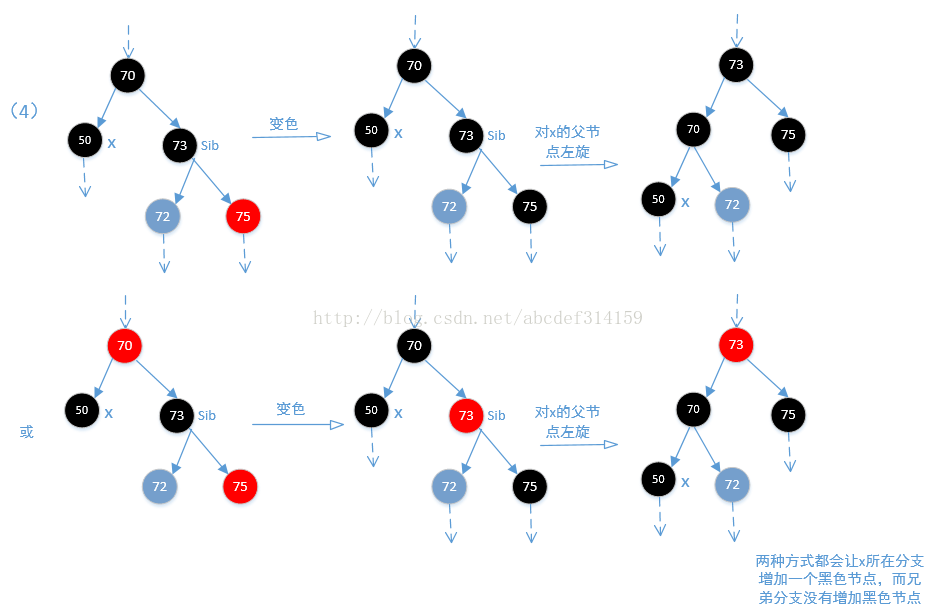
}OK,下面再来看一下fixAfterDeletion方法,因为x所在分支少了一个黑色的节点,所以他的主要目的就是让x分支增加一个黑色节点。这个比fixAfterInsertion方法还难理解,看代码
/** From CLR */
private void fixAfterDeletion(TreeMapEntry<K,V> x) {
//再看这个方法之前先看一下最后一行代码,他会把x节点设置为黑色
//很明显,在x只有黑色的时候才会调整,因为删除黑色打破了红黑平衡,但deleteEntry方法中的删除有两种,
//一种是替换之后的replacement,这个replacement不是删除的节点,需要删除的节点在这之前就已经被删除,
//他是来找平衡的,因为删除之后在这一分支上少了一个黑色节点,如果replacement节点为红色,那么不用执行
// while循环,直接在最后把它置为黑色就正好弥补了删除的黑色节点,如果replacement是黑色,那么需要执行
//下面的while循环(前提是replacement不等于root)。还一种就是没有子节点的,先调整完在删除,如果他是
//红色,就不用执行while循环,直接删除就是了,下面置不置为黑色都一样,如果是黑色,就必须执行下面的方法,
//因为删除黑色会打破红黑平衡。
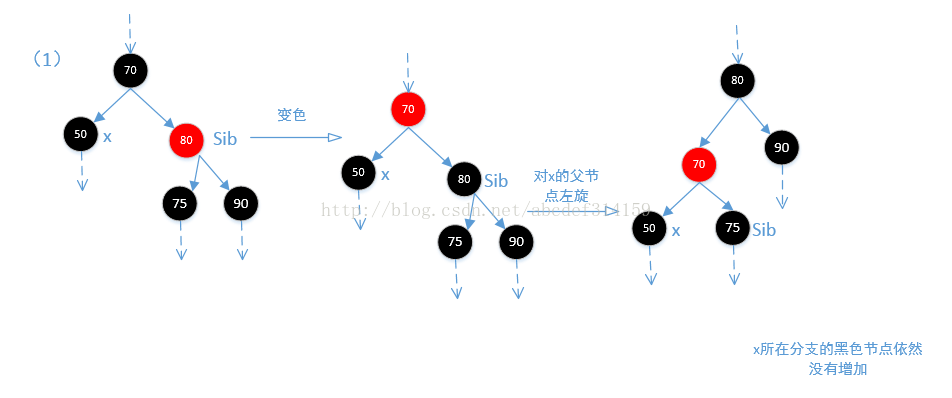
while (x != root && colorOf(x) == BLACK) {
//x是父节点的左节点
if (x == leftOf(parentOf(x))) {
TreeMapEntry<K,V> sib = rightOf(parentOf(x));//x的兄弟节点
//(1)兄弟节点是红色,这种情况下兄弟节点的父节点和子节点都一定是黑色的,
//然后让兄弟节点变为黑色,父节点变为红色,这种情况下从root节点到兄弟节点的各叶子节点黑色个数没有变化,
//但从root节点到x节点的黑色个数少了1(如果删除的是黑色节点,那么传进来的replacement分支上其实就已经少
//了一个黑色,但这里减少只是相对于传进来的x来说的,是相对的。),然后通过左旋,达到各分支上的黑色
//节点一致。
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));//左旋
//通过左旋,x的位置已经改变,但这里sib还是等于x的兄弟节点。
sib = rightOf(parentOf(x));
}
//其实执行到这一步往后可以认为x所在分支少了一个黑色节点。并且兄弟节点sib是黑色的
//(2)首先可以肯定一点的是sib节点肯定是黑色的,通过(1)及上面代码可以明白,如果sib是红色,那么他的子节
//点是黑色的,经过上面的左旋调整,sib的子节点会变为sib,也就是黑色。这里如果sib的两个子节点都是黑色的,那么
//让sib为红色,这样一来x分支和他兄弟分支sib都相当于少了一个黑色节点,所以从root节点到x分支和到sib分支的黑色
//节点都是一样的。那么问题来了,从root节点到x和sib分支的黑色节点比到其他分支的黑色节点明显是少了一个黑色节点,
//但是后面又让x等于x的父节点,所以如果父节点为红色,则跳出循环,在最后再变为黑色,此时所有的节点都又达到平衡,
//如果为黑色,则继续循环。
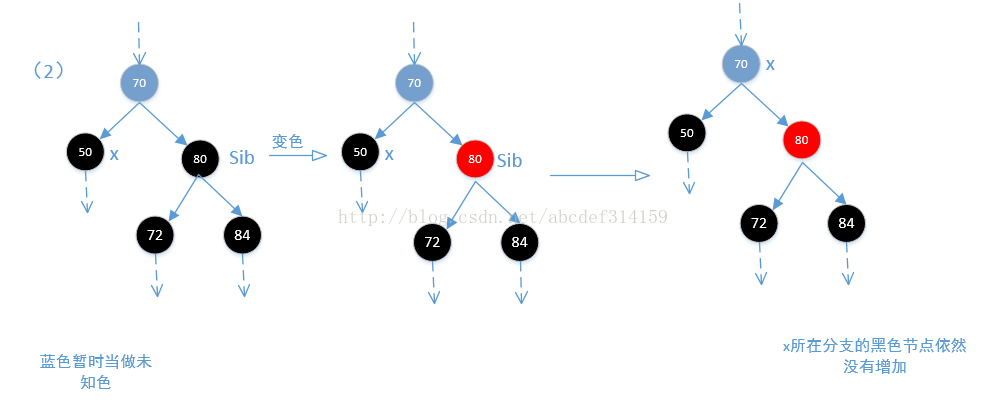
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
//(3)如果sib的右子节点是黑色,左子节点是红色(如果两个都是黑色则执行上面),这样不能直接让sib节点变为红色,因为
//这样会打破平衡.这个时候需要让左子节点变黑色,sib节点再变为红色。如果这样,那么问题就来了,因为这样从root到
//sib左分支的黑色节点是没有变化,但从root到sib右分支的黑色节点明显是少了一个黑色节点,然后再对sib进行右旋,
//让sib的左右子节点又各自达到平衡。然后在重新定位sib节点。但即使这样,从root到x节点的分支依然少了一个黑色节点。
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
//(4)由上上面可知sib是黑色的,即使sib的右节点为黑色,通过上面的改变颜色及旋转到最后sib还是黑色。sib的右节点是红色,
//如果是黑色,那么执行上面也会变为黑色,可以看一下下面的图(3).执行到这一步,从root
//到sib分支的黑色节点是没有变化,但从root到x分支的黑色节点是少了一个,然后执行下面的代码会使x的兄弟分支黑色节点不变
//x分支黑色节点加1,最终达到平衡。然后让x等于root,退出循环。最后是对root置为黑色,基本没有影响(因为root节点
//本来就是黑色),这里的代码让sib的颜色等于x父节点的颜色,基本没影响,其实他最终目的是让x所在分支增加一个黑色节点,
//来达到红黑平衡。
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
} else { // symmetric
//对称的,x是父节点的右节点的情况。
TreeMapEntry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);//最后把x节点置为黑色
}结合上面代码看一下下面的四张图
OK,到现在为止put和move方法都已经分析完了,下面看一下其他方法,
/**
* Returns the first Entry in the TreeMap (according to the TreeMap's
* key-sort function). Returns null if the TreeMap is empty.
*/
//返回第一个节点,最左边的,也是最小值
final TreeMapEntry<K,V> getFirstEntry() {
TreeMapEntry<K,V> p = root;
if (p != null)
while (p.left != null)
p = p.left;
return p;
}
/**
* Returns the last Entry in the TreeMap (according to the TreeMap's
* key-sort function). Returns null if the TreeMap is empty.
*/
//返回最后一个节点,最右边的,也是最大值
final TreeMapEntry<K,V> getLastEntry() {
TreeMapEntry<K,V> p = root;
if (p != null)
while (p.right != null)
p = p.right;
return p;
}再来看一下containsValue方法
//通过不停的循环查找,先从第一个查找,getFirstEntry()返回的是树的最小值,如果不等,再找比e大的最小值
//successor(e)返回的是e的后继节点,其实就是比e大的最小值,他还可以用于输出排序的大小
public boolean containsValue(Object value) {
for (TreeMapEntry<K,V> e = getFirstEntry(); e != null; e = successor(e))
if (valEquals(value, e.value))
return true;
return false;
}再来看一个getCeilingEntry,这个方法比较绕
/**
* Gets the entry corresponding to the specified key; if no such entry
* exists, returns the entry for the least key greater than the specified
* key; if no such entry exists (i.e., the greatest key in the Tree is less
* than the specified key), returns {@code null}.
*/
//返回最小key大于或等于指定key的节点。
final TreeMapEntry<K,V> getCeilingEntry(K key) {
TreeMapEntry<K,V> p = root;
while (p != null) {
int cmp = compare(key, p.key);
//指定key的节点小于查找的p节点,如果p的左节点(左节点比p小)存在就继续循环,如果不存在就返回p
if (cmp < 0) {
if (p.left != null)
p = p.left;
else
return p;//p节点比key的节点大
} else if (cmp > 0) {//指定的节点大于p节点
if (p.right != null) {//说明key节点比p节点大,如果p的右节点存在,就继续循环,查找更大的
p = p.right;
} else {
//p没有右节点,因为p的左节点是小于p的,既然查找的比p大,所以就往上找p的父节点,因为父节点也比右子节点小,所以要查找到
//父节点是父父节点的左节点为止,这个和查找后继节点其实类似,下面停止循环的条件要么是parent为null,要么ch是父节点的左节点,
//这个可能比较绕,我们先记下面循环停止的父节点是father节点(下面停止的条件是下一个循环的节点是father节点的左节点),在上
//面的循环中,能走到father的左节点这条路线,说明key的节点是小于father节点的,而沿着father节点的左分支一直找下去也没找到大
//于key的节点,这说明father的左节点都是小于key的,所以最后只能网上查找,找到father节点返回。
TreeMapEntry<K,V> parent = p.parent;
TreeMapEntry<K,V> ch = p;
while (parent != null && ch == parent.right) {//如果不为null,是左节点的时候停止循环
ch = parent;
parent = parent.parent;
}
return parent;
}
} else
return p;//如果存在直接返回
}
return null;
}下面再来看一个和getCeilingEntry方法类似的方法getFloorEntry。
/**
* Gets the entry corresponding to the specified key; if no such entry
* exists, returns the entry for the greatest key less than the specified
* key; if no such entry exists, returns {@code null}.
*/
//返回最大key小于或等于指定key的节点。
final TreeMapEntry<K,V> getFloorEntry(K key) {
TreeMapEntry<K,V> p = root;
while (p != null) {
int cmp = compare(key, p.key);
if (cmp > 0) {//指定的key大于查找的p,就是查找的p小了
if (p.right != null)//如果存在就循环,查找最大的
p = p.right;
else
return p;//否则就返回p,这个p是小于key的
} else if (cmp < 0) {//说明查找的p大于指定的key,就是查找的p大了
if (p.left != null) {//既然大了,那就往小的找
p = p.left;
} else {
TreeMapEntry<K,V> parent = p.parent;
TreeMapEntry<K,V> ch = p;
//往上找,停止的条件是parent为null,或者ch是父节点的右节点,其实这个方法和getCeilingEntry方法
//非常相似,能走到这一步说明他的父节点比key的大,所以才往左走,当他没有左节点的时候,说明没有
//找到比他小的,但是父节点是比他大的不合适,所以一直往上查找,当查到父节点是父父节点的右节点的
//时候返回,我们暂时记这个父父节点为father,当沿着father的右节点查找的时候,说明key是比father的
//右节点大的,当沿着father的左节点查找的时候说明是要查找比key的小的,但直到最后也没找到的时候,说明
//father的右分支都是都是比key的大,注意只好往上查找,找到father节点,因为father节点是比key的小。
while (parent != null && ch == parent.left) {
ch = parent;
parent = parent.parent;
}
return parent;
}
} else
return p;//正好找到,直接返回
}
return null;
}getHigherEntry函数和getCeilingEntry函数有点类似,不同点是如果有相同的key,getCeilingEntry会直接返回,而getHigherEntry仍然会返回比key大的最小节点,
同理getLowerEntry函数和getFloorEntry函数很相似,这里就不在详述。下面在看一个方法predecessor
/**
* Returns the predecessor of the specified Entry, or null if no such.
*/
static <K,V> TreeMapEntry<K,V> predecessor(TreeMapEntry<K,V> t) {
//这个和successor相反,他返回的是前继节点。后继节点返回的是大于t的最小节点,而前继节点返回的是小于
// t的最大节点
if (t == null)
return null;
else if (t.left != null) {//查找t的左节点是最右节点,其实也就是返回小于t的最大值
TreeMapEntry<K,V> p = t.left;
while (p.right != null)
p = p.right;
return p;
} else {
//如果t没有左左子节点,则只能往上找了,因为右节点是大于的,所以不合适,那么往上找也是大于的,那么就只有一个
//找到父节点是父父节点是右节点,返回这个父父节点就行了,这个如果不好理解可以看一下getFloorEntry函数的注释。
//因为一个节点的右节点及右节点的子节点都是大于当前节点的,所以当往左没有找到的时候就往上找,直到找到一个节点是
//父节点的右节点的时候,这个父节点就是小于t的最大节点,这时返回父节点。
TreeMapEntry<K,V> p = t.parent;
TreeMapEntry<K,V> ch = t;
while (p != null && ch == p.left) {
ch = p;
p = p.parent;
}
return p;
}
}OK,目前为止TreeMap主要方法都已整理完毕。
参阅:Java 集合系列12之 TreeMap详细介绍(源码解析)和使用示例
二叉查找树由于可能会非常的不均衡. 所以用2-3树. 采用上上浮的方法,顶多多两倍节点数.
红黑树一直是数据结构中的难点,大部分关于算法与数据结构的学习资料(包括《算法导论》)对于这部分的讲解都是上来就下定义,告诉我们红黑树这个性质那个性质,插入删除要注意1234点,但是基本没有讲为什么这样定义红色和黑色,让人理解起来十分费力。直到我看了下图这本书中关于红黑树部分的讲解,一时间豁然开朗,上网查了下这本书的作者Sedgewick,他是伟大的高德纳的学生!红黑树的发明者!
他在这本书中告诉了我们红黑树的根本模型:以二叉树的形式实现2-3树,通过红黑树与2-3树之间的一一对应,让我们对红黑树有了更直观的理解。
这本书里所讲的是左偏红黑树模型,理解了这个模型,再理解算法导论的完整红黑树模型就容易的多了。
Sedgewick是红黑树的发明者,1987年。因为平衡二叉树在插入和删除过程中需要判断插入的结点时2-结点还是3-结点等等一系列问题,实现起来代码量特别大,并且会增加额外开销,所以就提出了红黑树。
- Left-Leaning Red-Black Trees, Dagstuhl Workshop on Data Structures, Wadern, Germany, February, 2008,直接下载:http://www.cs.princeton.edu/~rs/talks/LLRB/RedBlack.pdf。
红黑树
红黑树的基本思想是用标准的二叉查找树(完全由2-结点构成)和一些额外的信息(替换3-结点)来表示2-3树。
2-3查找树
为了保证查找树的平衡性,我们需要一些灵活性,因此在这里我们允许树中的一个结点保存多个键。
2-结点:含有一个键(及值)和两条链接,左链接指向的2-3树中的键都小于该结点,右链接指向的2-3树中的键都大于该结点。
3-结点:含有两个键(及值)和三条链接,左链接指向的2-3树中的键都小于该结点,中链接指向的2-3树中的键都位于该结点的两个键之间,右链接指向的2-3树中的键都大于该结点。
(2-3指的是2叉-3叉的意思)
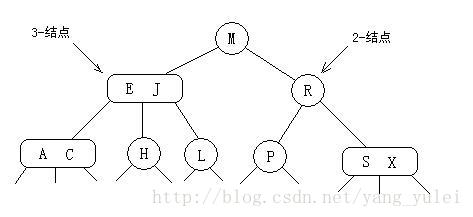

一颗完美平衡的2-3查找树中的所有空链接到根结点的距离都是相同的。
查找
要判断一个键是否在树中,我们先将它和根结点中的键比较。如果它和其中的任何一个相等,查找命中。否则我们就根据比较的结果找到指向相应区间的链接,并在其指向的子树中递归地继续查找。如果这是个空链接,查找未命中。
插入
要在2-3树中插入一个新结点,我们可以和二叉查找树一样先进行一次未命中的查找,然后把新结点挂在树的底部。但这样的话树无法保持完美平衡性。我们使用2-3树的主要原因就在于它能够在插入之后继续保持平衡。
如果未命中的查找结束于一个2-结点,我们只要把这个2-结点替换为一个3-结点,将要插入的键保存在其中即可。如果未命中的查找结束于一个3-结点,事情就要麻烦一些。
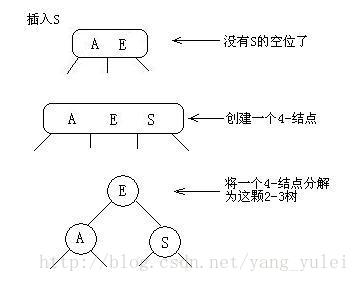
热身:
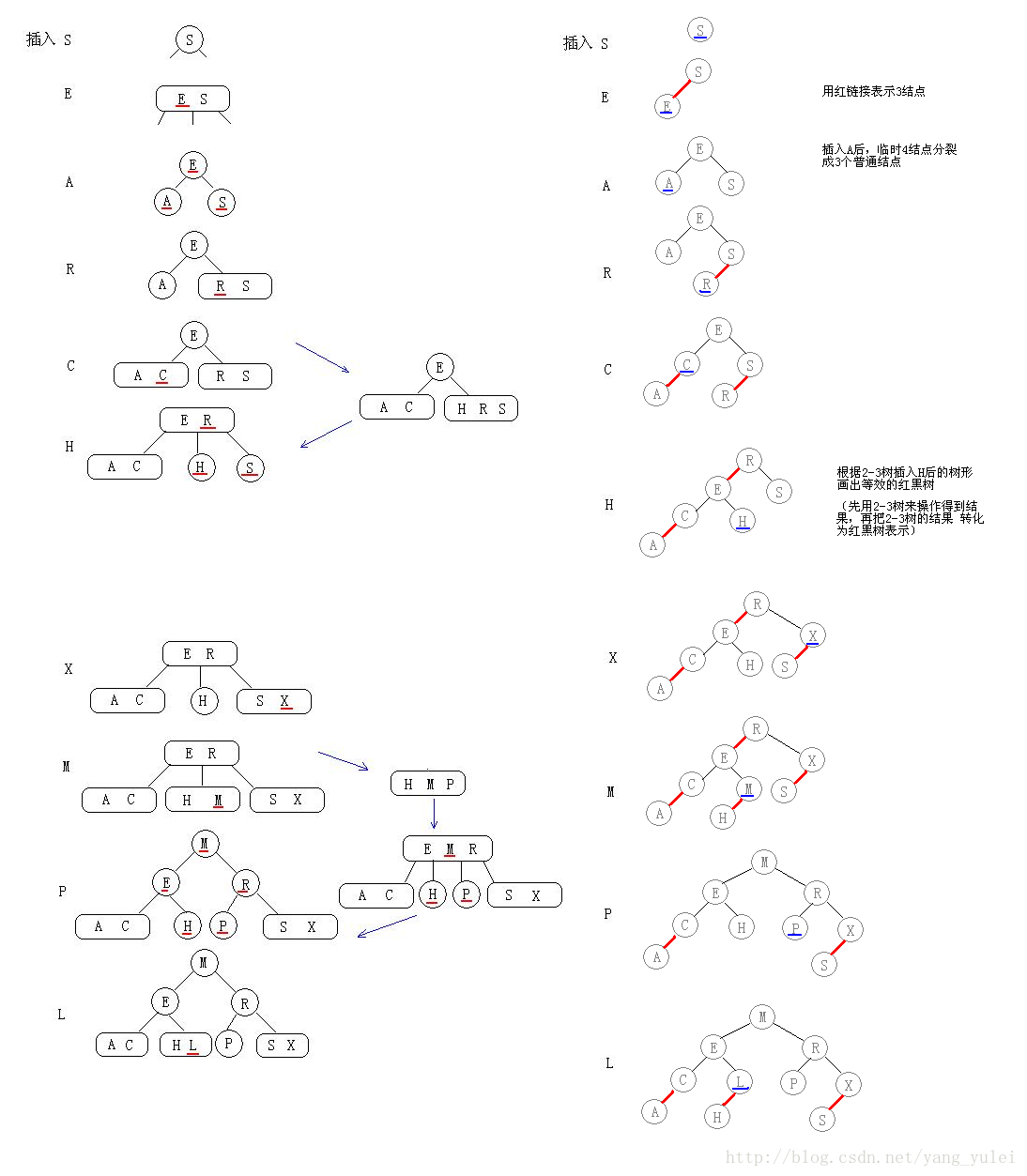
先考虑最简单的例子:只有一个3-结点的树,向其插入一个新键。
这棵树唯一的结点中已经没有可插入的空间了。我们又不能把新键插在其空结点上(破坏了完美平衡)。为了将新键插入,我们先临时将新键存入该结点中,使之成为一个4-结点。创建一个4-结点很方便,因为很容易将它转换为一颗由3个2-结点组成的2-3树(如图所示),这棵树既是一颗含有3个结点的二叉查找树,同时也是一颗完美平衡的2-3树,其中所有空链接到根结点的距离都相等。
向一个父结点为2-结点的3-结点中插入新键
假设未命中的查找结束于一个3-结点,而它的父结点是一个2-结点。在这种情况下我们需要在维持树的完美平衡的前提下为新键腾出空间。
我们先像刚才一样构造一个临时的4-结点并将其分解,但此时我们不会为中键创建一个新结点,而是将其移动至原来的父结点中。(如图所示)

这次转换也并不影响(完美平衡的)2-3树的主要性质。树仍然是有序的,因为中键被移动到父结点中去了,树仍然是完美平衡的,插入后所有的空链接到根结点的距离仍然相同。
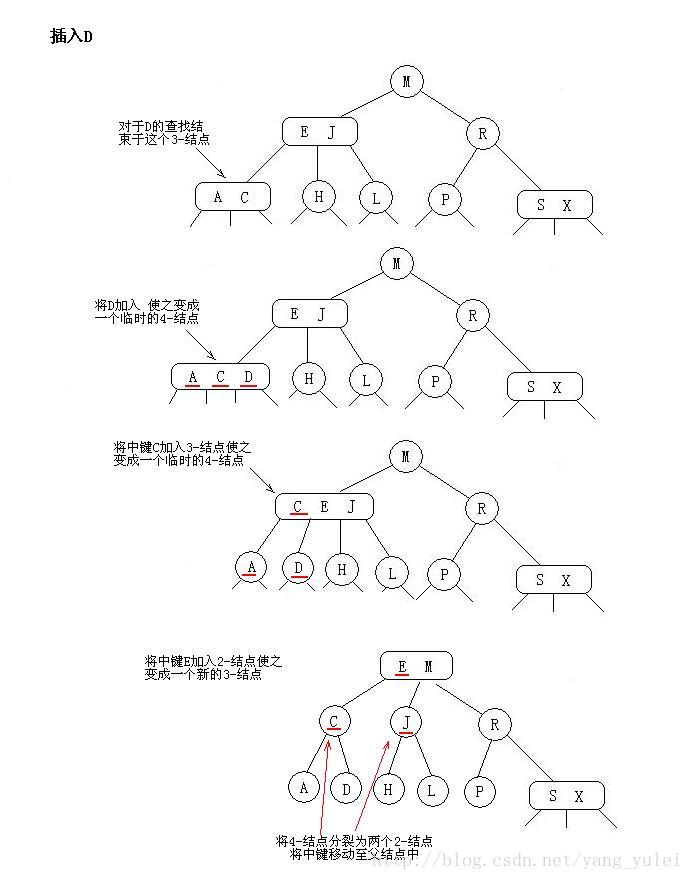
向一个父结点为3-结点的3-结点中插入新键
假设未命中的查找结束于一个3-结点,而它的父结点是一个3-结点。
我们再次和刚才一样构造一个临时的4-结点并分解它,然后将它的中键插入它的父结点中。但父结点也是一个3-结点,因此我们再用这个中键构造一个新的临时4-结点,然后在这个结点上进行相同的变换,即分解这个父结点并将它的中键插入到它的父结点中去。
我们就这样一直向上不断分解临时的4-结点并将中键插入更高的父结点,直至遇到一个2-结点并将它替换为一个不需要继续分解的3-结点,或者是到达3-结点的根。
总结:
先找插入结点,若结点有空(即2-结点),则直接插入。如结点没空(即3-结点),则插入使其临时容纳这个元素,然后分裂此结点,把中间元素移到其父结点中。对父结点亦如此处理。(中键一直往上移,直到找到空位,在此过程中没有空位就先搞个临时的,再分裂。)
★2-3树插入算法的根本在于这些变换都是局部的:除了相关的结点和链接之外不必修改或者检查树的其他部分。每次变换中,变更的链接数量不会超过一个很小的常数。所有局部变换都不会影响整棵树的有序性和平衡性。
{你确定理解了2-3树的插入过程了吗? 如果你理解了,那么你也就基本理解了红黑树的插入}
构造
和标准的二叉查找树由上向下生长不同,2-3树的生长是由下向上的。
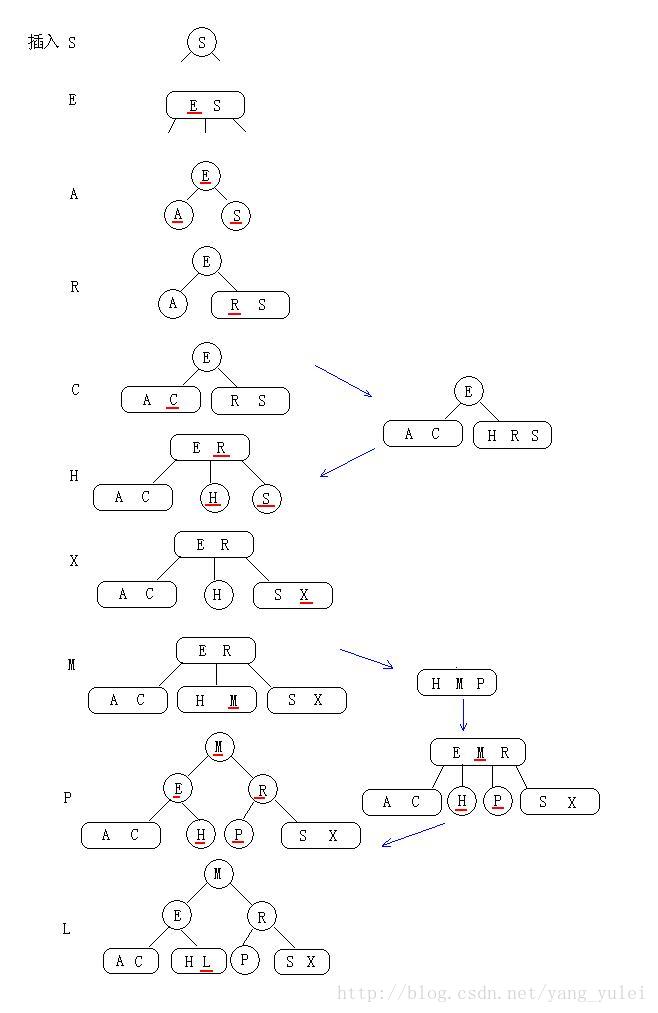
优点
2-3树在最坏情况下仍有较好的性能。每个操作中处理每个结点的时间都不会超过一个很小的常数,且这两个操作都只会访问一条路径上的结点,所以任何查找或者插入的成本都肯定不会超过对数级别。
完美平衡的2-3树要平展的多。例如,含有10亿个结点的一颗2-3树的高度仅在19到30之间。我们最多只需要访问30个结点就能在10亿个键中进行任意查找和插入操作。
缺点
我们需要维护两种不同类型的结点,查找和插入操作的实现需要大量的代码,而且它们所产生的额外开销可能会使算法比标准的二叉查找树更慢。
平衡一棵树的初衷是为了消除最坏情况,但我们希望这种保障所需的代码能够越少越好。
红黑二叉查找树
【前言:本文所讨论的红黑树之目的在于使读者能更简单清晰地了解红黑树的构造,使读者能在纸上清晰快速地画出红黑树,而不是为了写出红黑树的实现代码。
若是要在代码级理解红黑树,则势必需要记住其复杂的插入和旋转的各种情况,我认为那只有助于增加大家对红黑树的恐惧,实际面试和工作中几乎不会遇到需要自己动手实现红黑树的情况(很多语言的标准库中就有红黑树的实现)。 若对于红黑树的C代码实现有兴趣的,可移步至July的博客。】
(理解红黑树一句话就够了:红黑树就是用红链接表示3-结点的2-3树。那么红黑树的插入、构造就可转化为2-3树的问题,即:在脑中用2-3树来操作,得到结果,再把结果中的3-结点转化为红链接即可。而2-3树的插入,前面已有详细图文,实际也很简单:有空则插,没空硬插,再分裂。 这样,我们就不用记那么复杂且让人头疼的红黑树插入旋转的各种情况了。只要清楚2-3树的插入方式即可。 下面图文详细演示。)
红黑树的本质:
红黑树是对2-3查找树的改进,它能用一种统一的方式完成所有变换。
替换3-结点
★红黑树背后的思想是用标准的二叉查找树(完全由2-结点构成)和一些额外的信息(替换3-结点)来表示2-3树。
我们将树中的链接分为两种类型:红链接将两个2-结点连接起来构成一个3-结点,黑链接则是2-3树中的普通链接。确切地说,我们将3-结点表示为由一条左斜的红色链接相连的两个2-结点。
这种表示法的一个优点是,我们无需修改就可以直接使用标准二叉查找树的get()方法。对于任意的2-3树,只要对结点进行转换,我们都可以立即派生出一颗对应的二叉查找树。我们将用这种方式表示2-3树的二叉查找树称为红黑树。
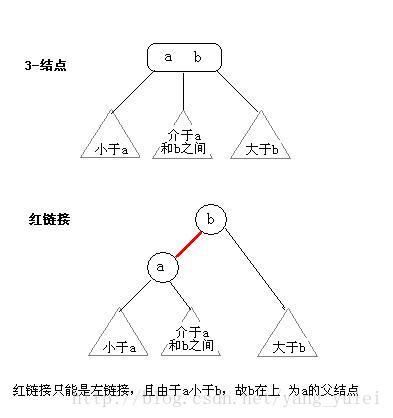
红黑树的另一种定义是满足下列条件的二叉查找树:
⑴红链接均为左链接。
⑵没有任何一个结点同时和两条红链接相连。
⑶该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑链接数量相同。
如果我们将一颗红黑树中的红链接画平,那么所有的空链接到根结点的距离都将是相同的。如果我们将由红链接相连的结点合并,得到的就是一颗2-3树。
相反,如果将一颗2-3树中的3-结点画作由红色左链接相连的两个2-结点,那么不会存在能够和两条红链接相连的结点,且树必然是完美平衡的。
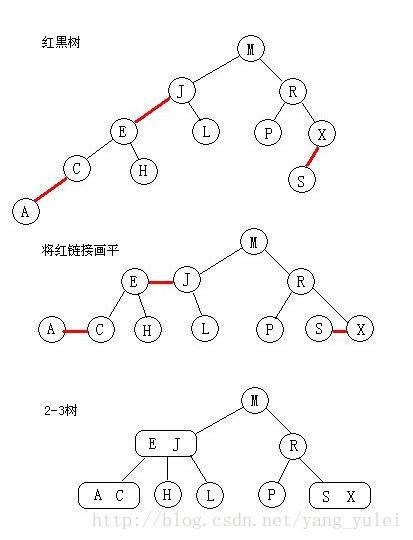
无论我们用何种方式去定义它们,红黑树都既是二叉查找树,也是2-3树。
(2-3树的深度很小,平衡性好,效率高,但是其有两种不同的结点,实际代码实现比较复杂。而红黑树用红链接表示2-3树中另类的3-结点,统一了树中的结点类型,使代码实现简单化,又不破坏其高效性。)
颜色表示:
因为每个结点都只会有一条指向自己的链接(从它的父结点指向它),我们将链接的颜色保存在表示结点的Node数据类型的布尔变量color中(若指向它的链接是红色的,那么该变量为true,黑色则为false)。
当我们提到一个结点颜色时,我们指的是指向该结点的链接的颜色。
旋转
在我们实现的某些操作中可能会出现红色右链接或者两条连续的红链接,但在操作完成前这些情况都会被小心地旋转并修复。
(我们在这里不讨论旋转的几种情况,把红黑树看做2-3树,自然可以得到正确的旋转后结果)
插入
在插入时我们可以使用旋转操作帮助我们保证2-3树和红黑树之间的一一对应关系,因为旋转操作可以保持红黑树的两个重要性质:有序性和完美平衡性。
热身:
向2-结点中插入新键
(向红黑树中插入操作时,想想2-3树的插入操作。红黑树与2-3树在本质上是相同的,只是它们对3结点的表示不同。
向一个只含有一个2-结点的2-3树中插入新键后,2-结点变为3-结点。我们再把这个3-结点转化为红结点即可)
向一颗双键树(即一个3-结点)中插入新键
(向红黑树中插入操作时,想想2-3树的插入操作。你把红黑树当做2-3树来处理插入,一切都变得简单了)
(向2-3树中的一个3-结点插入新键,这个3结点临时成为4-结点,然后分裂成3个2结点)

★一颗红黑树的构造全过程
平衡二叉树(AVL树)
定义:平衡二叉树(Balance Binary Tree)又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
若将二叉树上结点的平衡因子BF(BalanceFactor)定义为该结点的左子树深度减去它的右子树深度,则平衡因子的绝对值大于1。
其旋转操作 用2-3树的分裂来类比想象。
查找(二)简单清晰的B树、Trie树详解
查找(二)
散列表
散列表是普通数组概念的推广。由于对普通数组可以直接寻址,使得能在O(1)时间内访问数组中的任意位置。在散列表中,不是直接把关键字作为数组的下标,而是根据关键字计算出相应的下标。
使用散列的查找算法分为两步。第一步是用散列函数将被查找的键转化为数组的一个索引。
我们需要面对两个或多个键都会散列到相同的索引值的情况。因此,第二步就是一个处理碰撞冲突的过程,由两种经典解决碰撞的方法:拉链法和线性探测法。
散列表是算法在时间和空间上作出权衡的经典例子。
如果没有内存限制,我们可以直接将键作为(可能是一个超大的)数组的索引,那么所有查找操作只需要访问内存一次即可完成。但这种情况不会经常出现,因此当键很多时需要的内存太大。
另一方面,如果没有时间限制,我们可以使用无序数组并进行顺序查找,这样就只需要很少的内存。而散列表则使用了适度的空间和时间并在这两个极端之间找到了一种平衡。
●散列函数
我们面对的第一个问题就是散列函数的计算,这个过程会将键转化为数组的索引。我们要找的散列函数应该易于计算并且能够均匀分布所有的键。
散列函数和键的类型有关,对于每种类型的键我们都需要一个与之对应的散列函数。
正整数
将整数散列最常用的方法就是除留余数法。我们选择大小为素数M的数组,对于任意正整数k,计算k除以M的余数。(如果M不是素数,我们可能无法利用键中包含的所有信息,这可能导致我们无法均匀地散列值。)
浮点数
将键表示为二进制数,然后再使用除留余数法。(让浮点数的各个位都起作用)(Java就是这么做的)
字符串
除留余数法也可以处理较长的键,例如字符串,我们只需将它们当做大整数即可。即相当于将字符串当做一个N位的R进制值,将它除以M并取余。
·····软缓存
如果散列值的计算很耗时,那么我们或许可以将每个键的散列值缓存起来,即在每个键中使用一个hash变量来保存它的hashCode()返回值。
●基于拉链法的散列表
一个散列函数能够将键转化为数组索引。散列算法的第二步是碰撞处理,也就是处理两个或多个键的散列值相同的情况。
拉链法:将大小为M的数组中的每个元素指向一条链表,链表中的每个结点都存储了散列值为该元素的索引的键值对。
查找分两步:首先根据散列值找到对应的链表,然后沿着链表顺序查找相应的键。
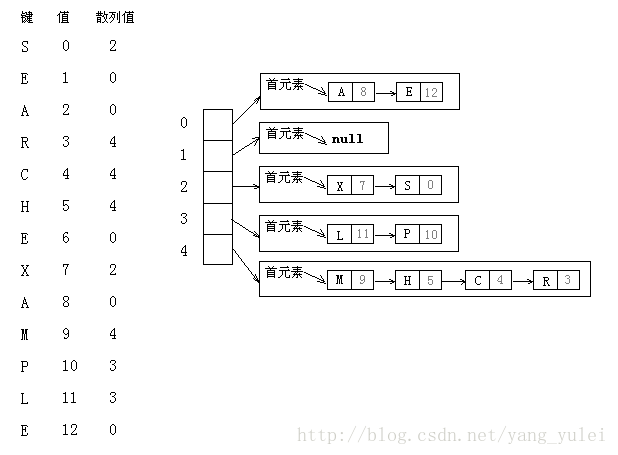
拉链法在实际情况中很有用,因为每条链表确实都大约含有N/M个键值对。
基于拉链法的散列表的实现简单。在键的顺序并不重要的应用中,它可能是最快的(也是使用最广泛的)符号表实现。
●基于线性探测法的散列表
实现散列表的另一种方式就是用大小为M的数组保存N个键值对,其中M>N。我们需要依靠数组中的空位解决碰撞冲突。基于这种策略的所有方法被统称为开放地址散列表。
开放地址散列表中最简单的方法叫做线性探测法:当碰撞发生时,我们直接检查散列表中的下一个位置(将索引值加1),如果不同则继续查找,直到找到该键或遇到一个空元素。
(开放地址类的散列表的核心思想是:与其将内存用作链表,不如将它们作为在散列表的空元素。这些空元素可以作为查找结束的标志。)
特点:散列最主要的目的在于均匀地将键散布开来,因此在计算散列后键的顺序信息就丢失了,如果你需要快速找到最大或最小的键,或是查找某个范围内的键,散列表都不是合适的选择。
【应用举例】
海量处理
给定a、b两个文件,各存放50亿个url,每个url各占64字节,内存限制是4G,让你找出a、b文件共同的url?
答:
可以估计每个文件安的大小为5G×64=320G,远远大于内存限制的4G。所以不可能将其完全加载到内存中处理。考虑采取分而治之的方法。
分而治之/hash映射:
遍历文件a,对每个url求取,然后根据所取得的值将url分别存储到1000个小文件(记为,这里漏写个了a1)中。这样每个小文件的大约为300M。遍历文件b,采取和a相同的方式将url分别存储到1000小文件中(记为)。这样处理后,所有可能相同的url都在对应的小文件()中,不对应的小文件不可能有相同的url。然后我们只要求出1000对小文件中相同的url即可。
hash_set统计:
求每对小文件中相同的url时,可以把其中一个小文件的url存储到hash_set中。然后遍历另一个小文件的每个url,看其是否在刚才构建的hash_set中,如果是,那么就是共同的url,存到文件里面就可以了。
(此题来源于v_July_v的博客)
B树(多向平衡查找树)
B-树是对2-3树数据结构的扩展。它支持对保存在磁盘或者网络上的符号表进行外部查找,这些文件可能比我们以前考虑的输入要大的多(以前的输入能够保存在内存中)。
(B树和B+树是实现数据库的数据结构,一般程序员用不到它。)
和2-3树一样,我们限制了每个结点中能够含有的“键-链接”对的上下数量界限:一个M阶的B-树,每个结点最多含有M-1对键-链接(假设M足够小,使得每个M向结点都能够存放在一个页中),最少含有M/2对键-链接,但也不能少于2对。
(B树是用于存储海量数据的,一般其一个结点就占用磁盘一个块的大小。)
【注】以下B树部分参考自July的博客,尤其是插入及删除示图,为了省力直接Copy自July。
B树中的结点存放的是键-值对。图中红色方块即为键对应值的指针。
B树中的每个结点根据实际情况可以包含大量的关键字信息和分支(当然是不能超过磁盘块的大小,根据磁盘驱动(diskdrives)的不同,一般块的大小在1k~4k左右);这样树的深度降低了,这就意味着查找一个元素只要很少结点从外存磁盘中读入内存,很快访问到要查找的数据。
查找
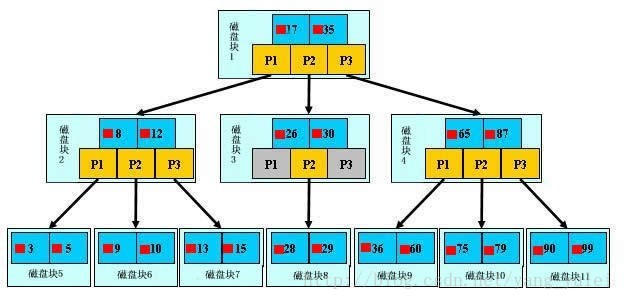
假如每个盘块可以正好存放一个B树的结点(正好存放2个文件名)。那么一个BTNODE结点就代表一个盘块,而子树指针就是存放另外一个盘块的地址。
下面,咱们来模拟下查找文件29的过程:
1. 根据根结点指针找到文件目录的根磁盘块1,将其中的信息导入内存。【磁盘IO操作1次】
2. 此时内存中有两个文件名17、35和三个存储其他磁盘页面地址的数据。根据算法我们发现:17<29<35,因此我们找到指针p2。
3. 根据p2指针,我们定位到磁盘块3,并将其中的信息导入内存。【磁盘IO操作 2次】
4. 此时内存中有两个文件名26,30和三个存储其他磁盘页面地址的数据。根据算法我们发现:26<29<30,因此我们找到指针p2。
5. 根据p2指针,我们定位到磁盘块8,并将其中的信息导入内存。【磁盘IO操作 3次】
6. 此时内存中有两个文件名28,29。根据算法我们查找到文件名29,并定位了该文件内存的磁盘地址。分析上面的过程,发现需要3 3次磁盘IO操作和次磁盘IO操作和3次内存查找 次内存查找操作。关于内存中的文件名查找,由于是一个有序表结构,可以利用折半查找提高效率。至于IO操作是影响整个B树查找效率的决定因素。
插入
想想2-3树的插入。2-3树结点的最大容量是2个元素,故当插入操作造成超出容量之后,就得分裂。同样m-阶B树规定的结点的最大容量是m-1个元素,故当插入操作造成超出容量之后也得分裂,其分裂成两个结点每个结点分m/2个元素。(副作用是在其父结点中要插入一个中间元素,用于分隔这两结点。和2-3树一样,再向父结点插入一个元素也可能会造成父结点的分裂,逐级向上操作,直到不再造成分裂为止。)
向某结点中插入一个元素使其分裂,可能会造成连锁反应,使其之上的结点也可能造成分裂。
总结:在B树中插入关键码key的思路:
对高度为h的m阶B树,新结点一般是插在第h层。通过检索可以确定关键码应插入的结点位置。然后分两种情况讨论:
1、 若该结点中关键码个数小于m-1,则直接插入即可。
2、 若该结点中关键码个数等于m-1,则将引起结点的分裂。以中间关键码为界将结点一分为二,产生一个新结点,并把中间关键码插入到父结点(h-1层)中
重复上述工作,最坏情况一直分裂到根结点,建立一个新的根结点,整个B树增加一层。
【例】
1、下面咱们通过一个实例来逐步讲解下。插入以下字符字母到一棵空的B 树中(非根结点关键字数小了(小于2个)就合并,大了(超过4个)就分裂):C N G A H E K Q M F W L T Z D P R X Y S,首先,结点空间足够,4个字母插入相同的结点中,如下图:
2、当咱们试着插入H时,结点发现空间不够,以致将其分裂成2个结点,移动中间元素G上移到新的根结点中,在实现过程中,咱们把A和C留在当前结点中,而H和N放置新的其右邻居结点中。如下图:

3、当咱们插入E,K,Q时,不需要任何分裂操作
4、插入M需要一次分裂,注意M恰好是中间关键字元素,以致向上移到父节点中
5、插入F,W,L,T不需要任何分裂操作

6、插入Z时,最右的叶子结点空间满了,需要进行分裂操作,中间元素T上移到父节点中,注意通过上移中间元素,树最终还是保持平衡,分裂结果的结点存在2个关键字元素。
7、插入D时,导致最左边的叶子结点被分裂,D恰好也是中间元素,上移到父节点中,然后字母P,R,X,Y陆续插入不需要任何分裂操作(别忘了,树中至多5个孩子)。
8、最后,当插入S时,含有N,P,Q,R的结点需要分裂,把中间元素Q上移到父节点中,但是情况来了,父节点中空间已经满了,所以也要进行分裂,将父节点中的中间元素M上移到新形成的根结点中,注意以前在父节点中的第三个指针在修改后包括D和G节点中。这样具体插入操作的完成,下面介绍删除操作,删除操作相对于插入操作要考虑的情况多点。

删除(delete)操作
首先查找B树中需删除的元素,如果该元素在B树中存在,则将该元素在其结点中进行删除,如果删除该元素后,首先判断该元素是否有左右孩子结点,如果有,则上移孩子结点中的某相近元素(“左孩子最右边的节点”或“右孩子最左边的节点”)到父节点中,然后是移动之后的情况;如果没有,直接删除后,移动之后的情况。
删除元素,移动相应元素之后,如果某结点中元素数目(即关键字数)小于ceil(m/2)-1,则需要看其某相邻兄弟结点是否丰满(结点中元素个数大于ceil(m/2)-1)(还记得第一节中关于B树的第5个特性中的c点么?: c)除根结点之外的结点(包括叶子结点)的关键字的个数n必须满足: (ceil(m / 2)-1)<= n <=m-1。m表示最多含有m个孩子,n表示关键字数。在本小节中举的一颗B树的示例中,关键字数n满足:2<=n<=4),如果丰满,则向父节点借一个元素来满足条件;如果其相邻兄弟都刚脱贫,即借了之后其结点数目小于ceil(m/2)-1,则该结点与其相邻的某一兄弟结点进行“合并”成一个结点,以此来满足条件。那咱们通过下面实例来详细了解吧。
以上述插入操作构造的一棵5阶B树(树中最多含有m(m=5)个孩子,因此关键字数最小为ceil(m/ 2)-1=2。还是这句话,关键字数小了(小于2个)就合并,大了(超过4个)就分裂)为例,依次删除H,T,R,E。
1、首先删除元素H,当然首先查找H,H在一个叶子结点中,且该叶子结点元素数目3大于最小元素数目ceil(m/2)-1=2,则操作很简单,咱们只需要移动K至原来H的位置,移动L至K的位置(也就是结点中删除元素后面的元素向前移动)
2、下一步,删除T,因为T没有在叶子结点中,而是在中间结点中找到,咱们发现他的继承者W(字母升序的下个元素),将W上移到T的位置,然后将原包含W的孩子结点中的W进行删除,这里恰好删除W后,该孩子结点中元素个数大于2,无需进行合并操作。
3、下一步删除R,R在叶子结点中,但是该结点中元素数目为2,删除导致只有1个元素,已经小于最小元素数目ceil(5/2)-1=2,而由前面我们已经知道:如果其某个相邻兄弟结点中比较丰满(元素个数大于ceil(5/2)-1=2),则可以向父结点借一个元素,然后将最丰满的相邻兄弟结点中上移最后或最前一个元素到父节点中(有没有看到红黑树中左旋操作的影子?),在这个实例中,右相邻兄弟结点中比较丰满(3个元素大于2),所以先向父节点借一个元素W下移到该叶子结点中,代替原来S的位置,S前移;然后X在相邻右兄弟结点中上移到父结点中,最后在相邻右兄弟结点中删除X,后面元素前移。
4、最后一步删除E, 删除后会导致很多问题,因为E所在的结点数目刚好达标,刚好满足最小元素个数(ceil(5/2)-1=2),而相邻的兄弟结点也是同样的情况,删除一个元素都不能满足条件,所以需要该节点与某相邻兄弟结点进行合并操作;首先移动父结点中的元素(该元素在两个需要合并的两个结点元素之间)下移到其子结点中,然后将这两个结点进行合并成一个结点。所以在该实例中,咱们首先将父节点中的元素D下移到已经删除E而只有F的结点中,然后将含有D和F的结点和含有A,C的相邻兄弟结点进行合并成一个结点。
5、也许你认为这样删除操作已经结束了,其实不然,在看看上图,对于这种特殊情况,你立即会发现父节点只包含一个元素G,没达标(因为非根节点包括叶子结点的关键字数n必须满足于2=<n<=4,而此处的n=1),这是不能够接受的。如果这个问题结点的相邻兄弟比较丰满,则可以向父结点借一个元素。假设这时右兄弟结点(含有Q,X)有一个以上的元素(Q右边还有元素),然后咱们将M下移到元素很少的子结点中,将Q上移到M的位置,这时,Q的左子树将变成M的右子树,也就是含有N,P结点被依附在M的右指针上。所以在这个实例中,咱们没有办法去借一个元素,只能与兄弟结点进行合并成一个结点,而根结点中的唯一元素M下移到子结点,这样,树的高度减少一层。
为了进一步详细讨论删除的情况,再举另外一个实例:
这里是一棵不同的5序B树,那咱们试着删除C
于是将删除元素C的右子结点中的D元素上移到C的位置,但是出现上移元素后,只有一个元素的结点的情况。
又因为含有E的结点,其相邻兄弟结点才刚脱贫(最少元素个数为2),不可能向父节点借元素,所以只能进行合并操作,于是这里将含有A,B的左兄弟结点和含有E的结点进行合并成一个结点。

这样又出现只含有一个元素F结点的情况,这时,其相邻的兄弟结点是丰满的(元素个数为3>最小元素个数2),这样就可以想父结点借元素了,把父结点中的J下移到该结点中,相应的如果结点中J后有元素则前移,然后相邻兄弟结点中的第一个元素(或者最后一个元素)上移到父节点中,后面的元素(或者前面的元素)前移(或者后移);注意含有K,L的结点以前依附在M的左边,现在变为依附在J的右边。这样每个结点都满足B树结构性质。
从以上操作可看出:除根结点之外的结点(包括叶子结点)的关键字的个数n满足:(ceil(m / 2)-1)<= n <= m-1,即2<=n<=4。这也佐证了咱们之前的观点。删除操作完。
(我思:)
(1、 关于B树中指针的表示。指针就是线索,是为了指示你找到目标。在内存中用内存的线性地址表示,在磁盘上,用磁盘的柱面和磁道号表示。
(2、 B树也是一种文件组织形式。它与OS文件系统的区别是,文件系统是面向磁盘上各种应用的文件的,所有文件的索引都被组织在一个系统文件表中。这样,一个相关应用的文件之间就没有体现有序性,我们对某组相关的文件进行查找,效率就会较低。 而B树是专门对某组相关的文件进行组织,使其之间相对有序,提高查找效率。 --尤其是对于需要频繁查找访问文件的操作。
例如: 对10亿个有序数,其分布在1000个文件中。普通的查找(类2分查找),和构造一个B树,普通的二分查找不仅需要多次访问文件,且其通过OS的文件系统通过文件名来访问文件,这样效率低——OS需要在整张系统文件表中通过文件名查找文件。 而B树,其是多叉树,树的深度比二分树要小很多,需要查找的文件比二分查找需要的少。且其通过自己建立的B树来索引文件(每次查找文件都通过该B树得到文件在磁盘上的位置)。B树是独立于OS的文件系统的,它中的每个文件都有相应的磁盘位置,而不仅是文件名。
B+树
B+ tree:是应文件系统所需而产生的一种B-tree的变形树。
一棵m阶的B+树和m阶的B树的异同点在于:
1、有n棵子树的结点中含有n-1 个关键字; (与B 树n棵子树有n-1个关键字 保持一致,)
2、所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接。
3、所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字。
【总结:最大的区别在于,B树是像2-3树那样把数据分散到所有的结点中,而B+树的数据都集中在叶结点,上层结点只是数据的索引,并不包含数据信息】

【应用举例】
1、为什么说B+-tree比B 树更适合实际应用中操作系统的文件索引和数据库索引?
数据库索引采用B+树的主要原因是 B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题。正是为了解决这个问题,B+树应运而生。
B+树只要遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的,而B树需要遍历整棵树,效率太低。
2、B+-tree的应用: VSAM(虚拟存储存取法)文件
B树与B+树
走进搜索引擎的作者梁斌老师针对B树、B+树给出了他的意见(来源于July):
“B+树还有一个最大的好处,方便扫库,B树必须用中序遍历的方法按序扫库,而B+树直接从叶子结点挨个扫一遍就完了,B+树支持range-query非常方便,而B树不支持。这是数据库选用B+树的最主要原因。
比如要查 5-10之间的,B+树一把到5这个标记,再一把到10,然后串起来就行了,B树就非常麻烦。B树的好处,就是成功查询特别有利,因为树的高度总体要比B+树矮。不成功的情况下,B树也比B+树稍稍占一点点便宜。B树比如你的例子中查,17的话,一把就得到结果了。
有很多基于频率的搜索是选用B树,越频繁query的结点越往根上走,前提是需要对query做统计,而且要对key做一些变化。
另外B树也好B+树也好,根或者上面几层因为被反复query,所以这几块基本都在内存中,不会出现读磁盘IO,一般已启动的时候,就会主动换入内存。”
"mysql 底层存储是用B+树实现的,因为在内存中B+树是没有优势的,但是一到磁盘,B+树的威力就出来了"。
B+树是B树的变形,它把所有的附属数据都放在叶子结点中,只将关键字和子女指针保存于内结点,内结点完全是索引的功能,最大化了内结点的分支因子。不过是n个关键字对应着n个子女,子女中含有父辈的结点信息,叶子结点包含所有信息(内结点包含在叶子结点中,内结点没有指向“附属数据”的指针必须索引到叶子结点)。这样的话还有一个好处就是对于每个结点所需的索引次数都是相等的,保证了稳定性。
【B*树】
B*树是B+树的变体,在B+树非根和非叶子结点再增加指向兄弟的指针;B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3(代替B+树的1/2)。
在数据库中的应用及性能分析
上文说过,红黑树等数据结构也可以用来实现索引,但是文件系统及数据库系统普遍采用B/B+Tree作为索引结构。
因为索引本身也很大,不可能全部存储在内存中,因此索引往往以索引文件的形式存储的磁盘上。这样的话,索引查找过程中就要产生磁盘I/O消耗,相对于内存存取,I/O存取的消耗要高几个数量级,所以评价一个数据结构作为索引的优劣最重要的指标就是在查找过程中磁盘I/O操作次数的渐进复杂度。
由于存储介质的特性,磁盘本身存取就比主存慢很多,再加上机械运动耗费,磁盘的存取速度往往是主存的几百分之一,因此为了提高效率,要尽量减少磁盘I/O。为了达到这个目的,磁盘往往不是严格按需读取,而是每次都会预读,即使只需要一个字节,磁盘也会从这个位置开始,顺序向后读取一定长度的数据放入内存。这样做的理论依据是计算机科学中著名的局部性原理:
当一个数据被用到时,其附近的数据也通常会马上被使用。程序运行期间所需要的数据通常比较集中。
由于磁盘顺序读取的效率很高(不需要寻道时间,只需很少的旋转时间),因此对于具有局部性的程序来说,预读可以提高I/O效率。
预读的长度一般为页(page)的整倍数。页是计算机管理存储器的逻辑块,硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块,每个存储块称为一页(在许多操作系统中,页得大小通常为4k),主存和磁盘以页为单位交换数据。当程序要读取的数据不在主存中时,会触发一个缺页异常,此时系统会向磁盘发出读盘信号,磁盘会找到数据的起始位置并向后连续读取一页或几页载入内存中,然后异常返回,程序继续运行。
【下面分析B/B+Tree索引的性能】
我们使用磁盘I/O次数评价索引结构的优劣。先从B Tree分析,根据B Tree的定义,可知检索一次最多需要访问h个节点。数据库系统的设计者巧妙利用了磁盘预读原理,将一个节点的大小设为等于一个页,这样每个节点只需要一次I/O就可以完全载入。为了达到这个目的,在实际实现中B-Tree在每次新建节点时,直接申请一个页的空间,这样就保证一个节点物理上也存储在一个页里,加之计算机存储分配都是按页对齐的,就实现了一个node只需一次I/O。
B-Tree中一次检索最多需要h-1次I/O(根节点常驻内存),渐进复杂度为O(h)=O(logdN)。一般实际应用中,出度d是非常大的数字,通常超过100,因此h非常小(通常不超过3)。
综上所述,用B-Tree作为索引结构效率是非常高的。
而红黑树这种结构,h明显要深的多。由于逻辑上很近的节点(父子)物理上可能很远,无法利用局部性,所以红黑树的I/O渐进复杂度也为O(h),效率明显比B-Tree差很多。
B+Tree更适合外存索引,原因和内节点出度d有关。从上面分析可以看到,d越大索引的性能越好,而出度的上限取决于节点内key和data的大小,由于B+Tree内节点去掉了data域,因此可以拥有更大的出度,拥有更好的性能。
我应该使用符号表的哪种实现
对于典型的应用程序,应该在散列表和二叉查找树之间进行选择。
相对于二叉查找树,散列表的优点在于代码更简单,且查找时间最优(常数级别)。二叉查找树相对于散列表的优点在于抽象结构更简单(不需要设计散列函数),红黑树可以保证最坏情况下的性能且它能够支持的操作更多(如排名、选择和范围查找)。
大多数程序员的第一选择都是散列表,在其他因素更重要时才会选择红黑树。(”第一选择”的例外:当键都是长字符串时,我们可以构造出比红黑树更灵活而又比散列表更高效的数据结构 Trie树)
=================================================字符串的查找============================================
单词查找树(Trie树)
单词查找树的英文单词trie来自于E.Fredkin在1960年玩的一个文字游戏,因为这个数据结构的作用是取出(retrieval)数据,但发音为try是为了避免与tree相混淆。
基本性质:
每个结点都含有R条链接,其中R为字母表的大小。(单词查找树一般都含有大量的空链接,因此在绘制一颗单词查找树时一般会忽略空链接。)
树中的每个结点中不是包含一个或几个关键字,而是只含有组成关键字的符号。例如,若关键字是数值,则结点中只包含一个数位;若关键字是单词,则结点中只包含一个字母字符。我们将每个键所关联的值保存在该键的最后一个字母所对应的结点中。
(这种树会给某种类型关键字的表的查找带来方便。)
假设有如下关键字的集合
{ CAI、CAO、LI、LAN、CHA、CHANG、WEN、CHAO、YUN、YANG、LONG、WANG、ZHAO、LIU、WU、CHEN }

若以树的多重链表来表示Trie树,则树的每个结点中应含有d个指针域。
若从Trie树中某个结点到叶子结点的路径上每个结点都只有一个孩子,则可将该路径上所有结点压缩成一个“叶子结点”,且在该叶子结点中存储关键字及指向记录的指针等信息。

在Trie树中有两种结点:
分支结点:含有d个指针域和一个指示该结点中非空指针域的个数的整数域。(分支结点所表示的字符是由其指向子树指针的索引位置决定的)
叶子结点:含有关键字域和指向记录的指针域。
typedef structTrieNode
{
NodeKind kind ;
union {
struct {KeyType K; Record *infoptr} lf ; //叶子结点
struct {TrieNode *ptr[27]; int num} bh ; //分支结点
} ;
} TrieNode,*TrieTree ;
查找
在Trie树上进行查找的过程为:从根结点出发,沿给定值相应的指针逐层向下,直至叶子结点,若叶子结点中的关键字和给定值相等,则查找成功。若分支结点中和给定值相应的指针为空,或叶结点中的关键字和给定值不相等,则查找不成功。
分割
查找操作的时间依赖于树的深度。
我们可以对关键字集选择一种合适的分割,以缩减Trie树的深度。
例如:先按首字符不同分成多个子集之后,然后按最后一个字符不同分割每个子集,再按第二个字符……,前后交叉分割。
如下图:在该树上,除两个叶子结点在第四层上外,其余叶子结点均在第三层上。
若分割的合适,则可使每个叶子结点中只含有少数几个同义词。

插入和删除
在Trie树上易于进行插入和删除,只是需要相应地增加和删除一些分支结点。
把沿途分支结点中相应的指针域置空,再把其分支结点中的num-1,然后删除叶子结点。当分支结点中num域的值减为1时,便可删除。
【应用举例】
寻找热门查询,300万个查询字符串中统计最热门的10个查询。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号