Redis之压缩列表ziplist

Redis是基于内存的nosql，有些场景下为了节省内存redis会用“时间”换“空间”。
ziplist就是很典型的例子。

ziplist是list键、hash键以及zset键的底层实现之一（3.0之后list键已经不直接用ziplist和linkedlist作为底层实现了，取而代之的是quicklist）
这些键的常规底层实现如下：

• list键：双向链表
• hash键：字典dict
• zset键：跳跃表zskiplist

但是当list键里包含的元素较少、并且每个元素要么是小整数要么是长度较小的字符串时，redis将会用ziplist作为list键的底层实现。同理hash和zset在这种场景下也会使用ziplist。

既然已有底层结构可以实现list、hash、zset键，为什么还要用ziplist呢？
当然是为了节省内存空间
我们先来看看ziplist是如何压缩的

原理

整体布局

ziplist是由一系列特殊编码的连续内存块组成的顺序存储结构，类似于数组，ziplist在内存中是连续存储的，但是不同于数组，为了节省内存 ziplist的每个元素所占的内存大小可以不同（数组中叫元素，ziplist叫节点entry，下文都用“节点”），每个节点可以用来存储一个整数或者一个字符串。
下图是ziplist在内存中的布局

 

• zlbytes: ziplist的长度（单位: 字节)，是一个32位无符号整数
• zltail: ziplist最后一个节点的偏移量，反向遍历ziplist或者pop尾部节点的时候有用。
• zllen: ziplist的节点（entry）个数
• entry: 节点
• zlend: 值为0xFF，用于标记ziplist的结尾

普通数组的遍历是根据数组里存储的数据类型 找到下一个元素的，例如int类型的数组访问下一个元素时每次只需要移动一个sizeof(int)就行（实际上开发者只需让指针p+1就行，在这里引入sizeof(int)只是为了说明区别）。
上文说了，ziplist的每个节点的长度是可以不一样的，而我们面对不同长度的节点又不可能直接sizeof(entry)，那么它是怎么访问下一个节点呢？
ziplist将一些必要的偏移量信息记录在了每一个节点里，使之能跳到上一个节点或下一个节点。
接下来我们看看节点的布局

节点的布局(entry)

每个节点由三部分组成：prevlength、encoding、data

• prevlengh: 记录上一个节点的长度，为了方便反向遍历ziplist
• encoding: 当前节点的编码规则，下文会详细说
• data: 当前节点的值，可以是数字或字符串 

为了节省内存，根据上一个节点的长度prevlength 可以将ziplist节点分为两类：

 

• entry的前8位小于254，则这8位就表示上一个节点的长度
• entry的前8位等于254，则意味着上一个节点的长度无法用8位表示，后面32位才是真实的prevlength。用254 不用255(11111111)作为分界是因为255是zlend的值，它用于判断ziplist是否到达尾部。

根据当前节点存储的数据类型及长度，可以将ziplist节点分为9类：
其中整数节点分为6类： 

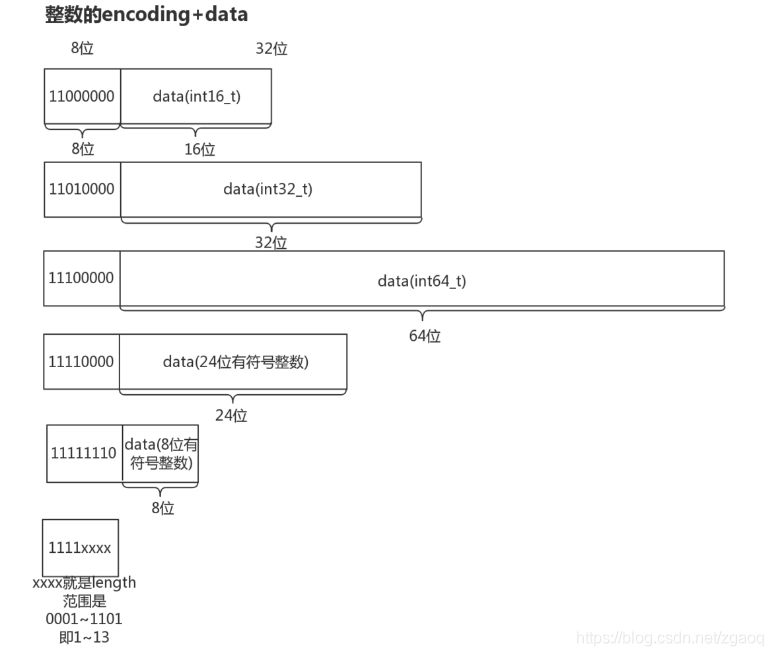
 整数节点的encoding的长度为8位，其中高2位用来区分整数节点和字符串节点（高2位为11时是整数节点），低6位用来区分整数节点的类型，定义如下:

1.  
   #define ZIP_INT_16B (0xc0 | 0<<4)//整数data,占16位（2字节）
2.  
   #define ZIP_INT_32B (0xc0 | 1<<4)//整数data,占32位（4字节）
3.  
   #define ZIP_INT_64B (0xc0 | 2<<4)//整数data,占64位（8字节）
4.  
   #define ZIP_INT_24B (0xc0 | 3<<4)//整数data,占24位（3字节）
5.  
   #define ZIP_INT_8B 0xfe //整数data,占8位（1字节）
6.  
   /* 4 bit integer immediate encoding */
7.  
   //整数值1~13的节点没有data，encoding的低四位用来表示data
8.  
   #define ZIP_INT_IMM_MASK 0x0f
9.  
   #define ZIP_INT_IMM_MIN 0xf1 /* 11110001 */
10.  
    #define ZIP_INT_IMM_MAX 0xfd /* 11111101 */

值得注意的是 最后一种encoding是存储整数0~12的节点的encoding，它没有额外的data部分，encoding的高4位表示这个类型，低4位就是它的data。这种类型的节点的encoding大小介于ZIP_INT_24B与ZIP_INT_8B之间（1~13），但是为了表示整数0，取出低四位xxxx之后会将其-1作为实际的data值（0~12）。在函数zipLoadInteger中，我们可以看到这种类型节点的取值方法：

1.  
   ...
2.  
   } else if (encoding >= ZIP_INT_IMM_MIN && encoding <= ZIP_INT_IMM_MAX) {
3.  
   ret = (encoding & ZIP_INT_IMM_MASK)-1;
4.  
   }
5.  
   ...

字符串节点分为3类：

• 当data小于63字节时(2^6)，节点存为上图的第一种类型，高2位为00，低6位表示data的长度。
• 当data小于16383字节时(2^14)，节点存为上图的第二种类型，高2位为01，后续14位表示data的长度。
• 当data小于4294967296字节时(2^32)，节点存为上图的第二种类型，高2位为10，下一字节起连续32位表示data的长度。

上图可以看出：
不同于整数节点encoding永远是8位，字符串节点的encoding可以有8位、16位、40位三种长度
相同encoding类型的整数节点 data长度是固定的，但是相同encoding类型的字符串节点，data长度取决于encoding后半部分的值。

1.  
   #define ZIP_STR_06B (0 << 6)//字符串data,最多有2^6字节(encoding后半部分的length有6位,length决定data有多少字节)
2.  
   #define ZIP_STR_14B (1 << 6)//字符串data,最多有2^14字节
3.  
   #define ZIP_STR_32B (2 << 6)//字符串data,最多有2^32字节

 

上文介绍了ziplist节点（entry）的分类，知道了节点可以细分为9种类型，那么当遍历一个ziplist时，指针到达某个节点时 如何判断出节点的类型从而找到data呢？

已知节点的位置，求data的值

根据图2 entry布局 可以看出，若要算出data的偏移量，得先计算出prevlength所占内存大小（1字节和5字节）：

1.  
   //根据ptr指向的entry，返回这个entry的prevlensize
2.  
   #define ZIP_DECODE_PREVLENSIZE(ptr, prevlensize) do { \
3.  
   if ((ptr)[0] < ZIP_BIGLEN) { \
4.  
   (prevlensize) = 1; \
5.  
   } else { \
6.  
   (prevlensize) = 5; \
7.  
   } \
8.  
   } while(0);

接着再用ZIP_DECODE_LENGTH(ptr + prevlensize, encoding, lensize, len)算出encoding所占的字节，返回给lensize；data所占的字节返回给len

1.  
   //根据ptr指向的entry求出该entry的len（encoding里存的 data所占字节）和lensize（encoding所占的字节）
2.  
   #define ZIP_DECODE_LENGTH(ptr, encoding, lensize, len) do { \
3.  
   ZIP_ENTRY_ENCODING((ptr), (encoding)); \
4.  
   if ((encoding) < ZIP_STR_MASK) { \
5.  
   if ((encoding) == ZIP_STR_06B) { \
6.  
   (lensize) = 1; \
7.  
   (len) = (ptr)[0] & 0x3f; \
8.  
   } else if ((encoding) == ZIP_STR_14B) { \
9.  
   (lensize) = 2; \
10.  
    (len) = (((ptr)[0] & 0x3f) << 8) | (ptr)[1]; \
11.  
    } else if (encoding == ZIP_STR_32B) { \
12.  
    (lensize) = 5; \
13.  
    (len) = ((ptr)[1] << 24) | \
14.  
    ((ptr)[2] << 16) | \
15.  
    ((ptr)[3] << 8) | \
16.  
    ((ptr)[4]); \
17.  
    } else { \
18.  
    assert(NULL); \
19.  
    } \
20.  
    } else { \
21.  
    (lensize) = 1; \
22.  
    (len) = zipIntSize(encoding); \
23.  
    } \
24.  
    } while(0);
25.  
     
26.  
    //将ptr的encoding解析成1个字节：00000000、01000000、10000000(字符串类型)和11??????(整数类型)
27.  
    //如果是整数类型，encoding直接照抄ptr的;如果是字符串类型，encoding被截断成一个字节并清零后6位
28.  
    #define ZIP_ENTRY_ENCODING(ptr, encoding) do { \
29.  
    (encoding) = (ptr[0]); \
30.  
    if ((encoding) < ZIP_STR_MASK) (encoding) &= ZIP_STR_MASK; \
31.  
    } while(0)
32.  
     
33.  
    //根据encoding返回数据(整数)所占字节数
34.  
    unsigned int zipIntSize(unsigned char encoding) {
35.  
    switch(encoding) {
36.  
    case ZIP_INT_8B: return 1;
37.  
    case ZIP_INT_16B: return 2;
38.  
    case ZIP_INT_24B: return 3;
39.  
    case ZIP_INT_32B: return 4;
40.  
    case ZIP_INT_64B: return 8;
41.  
    default: return 0; /* 4 bit immediate */
42.  
    }
43.  
    assert(NULL);
44.  
    return 0;
45.  
    }

完成以上步骤之后，即可算出data的位置:ptr+prevlensize+lensize，以及data的长度len

ziplist接口

上文已经阐述了ziplist的底层内存布局，接下来看看一些基本的增删改查操作在ziplist中是如何执行的。

ziplistNew 创建一个ziplist O(1)

1.  
   /* Create a new empty ziplist. */
2.  
   unsigned char *ziplistNew(void) {
3.  
   unsigned int bytes = ZIPLIST_HEADER_SIZE+1;//4字节4字节2字节1字节，没有entry节点
4.  
   unsigned char *zl = zmalloc(bytes);
5.  
   ZIPLIST_BYTES(zl) = intrev32ifbe(bytes);//赋值
6.  
   ZIPLIST_TAIL_OFFSET(zl) = intrev32ifbe(ZIPLIST_HEADER_SIZE);//
7.  
   ZIPLIST_LENGTH(zl) = 0;//
8.  
   zl[bytes-1] = ZIP_END;//
9.  
   return zl;
10.  
    }
11.  
    #define ZIPLIST_HEADER_SIZE (sizeof(uint32_t)*2+sizeof(uint16_t))//空ziplist除了的大小
12.  
    #define ZIPLIST_BYTES(zl) (*((uint32_t*)(zl)))//的指针的值，可读可写
13.  
    #define ZIPLIST_TAIL_OFFSET(zl) (*((uint32_t*)((zl)+sizeof(uint32_t))))//的指针的值
14.  
    #define ZIPLIST_HEADER_SIZE (sizeof(uint32_t)*2+sizeof(uint16_t))//空ziplist除了的大小
15.  
    #define ZIPLIST_LENGTH(zl) (*((uint16_t*)((zl)+sizeof(uint32_t)*2)))//的指针的值

参照着图1理解会直观些，分配了一块内存并初始化，没有entry。

ziplistFind 从ziplist里找出一个entry O(n)

1.  
   //返回p节点之后data与vstr(长度是vlen)相等的节点，只找p节点之后每隔skip的节点
2.  
   //时间复杂度 O(n)
3.  
   unsigned char *ziplistFind(unsigned char *p, unsigned char *vstr, unsigned int vlen, unsigned int skip) {
4.  
   int skipcnt = 0;
5.  
   unsigned char vencoding = 0;
6.  
   long long vll = 0;
7.  
    
8.  
   while (p[0] != ZIP_END) {
9.  
   unsigned int prevlensize, encoding, lensize, len;
10.  
    unsigned char *q;
11.  
     
12.  
    ZIP_DECODE_PREVLENSIZE(p, prevlensize);
13.  
    ZIP_DECODE_LENGTH(p + prevlensize, encoding, lensize, len);
14.  
    q = p + prevlensize + lensize;//当前节点的data
15.  
     
16.  
    if (skipcnt == 0) {
17.  
    /* Compare current entry with specified entry */
18.  
    if (ZIP_IS_STR(encoding)) {//判断当前节点是不是字符串节点
19.  
    if (len == vlen && memcmp(q, vstr, vlen) == 0) {
20.  
    return p;
21.  
    }
22.  
    } else {
23.  
    /* Find out if the searched field can be encoded. Note that
24.  
    * we do it only the first time, once done vencoding is set
25.  
    * to non-zero and vll is set to the integer value. */
26.  
    if (vencoding == 0) {//这个代码块只会执行一次,计算vstr的整数表示
27.  
    if (!zipTryEncoding(vstr, vlen, &vll, &vencoding)) {
28.  
    //将参数给的节点vstr当做整数节点转换；将data值返回给vll，节点编码返回给vencoding
29.  
    //进入这个代码块说明将vstr转换成整数失败，vencoding不变，下次判断当前节点是整数节点之后可以跳过这个节点
30.  
    /* If the entry can't be encoded we set it to
31.  
    * UCHAR_MAX so that we don't retry again the next
32.  
    * time. */
33.  
    vencoding = UCHAR_MAX;//当前节点是整数节点，但是vstr是字符串节点，跳过不用比较了
34.  
    }
35.  
    /* Must be non-zero by now */
36.  
    assert(vencoding);
37.  
    }
38.  
     
39.  
    /* Compare current entry with specified entry, do it only
40.  
    * if vencoding != UCHAR_MAX because if there is no encoding
41.  
    * possible for the field it can't be a valid integer. */
42.  
    if (vencoding != UCHAR_MAX) {
43.  
    long long ll = zipLoadInteger(q, encoding);//算出当前节点的data
44.  
    if (ll == vll) {
45.  
    return p;
46.  
    }
47.  
    }
48.  
    }
49.  
     
50.  
    /* Reset skip count */
51.  
    skipcnt = skip;
52.  
    } else {
53.  
    /* Skip entry */
54.  
    skipcnt--;
55.  
    }
56.  
     
57.  
    /* Move to next entry */
58.  
    p = q + len;
59.  
    }
60.  
     
61.  
    return NULL;
62.  
    }
63.  
     
64.  
    //尝试将entry地址的内容转换成整数，并根据这个整数算出一个合适的encoding返回给encoding参数。
65.  
    //若无法转换成整数，则encoding不变，返回0，等到下次调用zipEncodeLength时再计算一个该字符串的encoding
66.  
    int zipTryEncoding(unsigned char *entry, unsigned int entrylen, long long *v, unsigned char *encoding) {
67.  
    long long value;
68.  
     
69.  
    if (entrylen >= 32 || entrylen == 0) return 0;
70.  
    if (string2ll((char*)entry,entrylen,&value)) {
71.  
    /* Great, the string can be encoded. Check what's the smallest
72.  
    * of our encoding types that can hold this value. */
73.  
    if (value >= 0 && value <= 12) {
74.  
    *encoding = ZIP_INT_IMM_MIN+value;
75.  
    } else if (value >= INT8_MIN && value <= INT8_MAX) {
76.  
    *encoding = ZIP_INT_8B;
77.  
    } else if (value >= INT16_MIN && value <= INT16_MAX) {
78.  
    *encoding = ZIP_INT_16B;
79.  
    } else if (value >= INT24_MIN && value <= INT24_MAX) {
80.  
    *encoding = ZIP_INT_24B;
81.  
    } else if (value >= INT32_MIN && value <= INT32_MAX) {
82.  
    *encoding = ZIP_INT_32B;
83.  
    } else {
84.  
    *encoding = ZIP_INT_64B;
85.  
    }
86.  
    *v = value;
87.  
    return 1;
88.  
    }
89.  
    return 0;
90.  
    }
91.  
     
92.  
    /* Read integer encoded as 'encoding' from 'p' */
93.  
    int64_t zipLoadInteger(unsigned char *p, unsigned char encoding) {
94.  
    int16_t i16;
95.  
    int32_t i32;
96.  
    int64_t i64, ret = 0;
97.  
    if (encoding == ZIP_INT_8B) {
98.  
    ret = ((int8_t*)p)[0];
99.  
    } else if (encoding == ZIP_INT_16B) {
100.  
     memcpy(&i16,p,sizeof(i16));
101.  
     memrev16ifbe(&i16);
102.  
     ret = i16;
103.  
     } else if (encoding == ZIP_INT_32B) {
104.  
     memcpy(&i32,p,sizeof(i32));
105.  
     memrev32ifbe(&i32);
106.  
     ret = i32;
107.  
     } else if (encoding == ZIP_INT_24B) {
108.  
     i32 = 0;
109.  
     memcpy(((uint8_t*)&i32)+1,p,sizeof(i32)-sizeof(uint8_t));
110.  
     memrev32ifbe(&i32);
111.  
     ret = i32>>8;
112.  
     } else if (encoding == ZIP_INT_64B) {
113.  
     memcpy(&i64,p,sizeof(i64));
114.  
     memrev64ifbe(&i64);
115.  
     ret = i64;
116.  
     } else if (encoding >= ZIP_INT_IMM_MIN && encoding <= ZIP_INT_IMM_MAX) {
117.  
     ret = (encoding & ZIP_INT_IMM_MASK)-1;
118.  
     } else {
119.  
     assert(NULL);
120.  
     }
121.  
     return ret;
122.  
     }
123.  
     其他接口

• ziplistInsert 往ziplist里插入一个entry 时间复杂度 平均:O(n), 最坏:O(n²)
• ziplistDelete 从siplist里删除一个entry 时间复杂度 平均:O(n), 最坏:O(n²)

为什么插入节点和删除节点两个接口的最坏时间复杂度会是O(n²)呢？这是由于ziplist的“连锁更新”导致的，连锁更新在最坏情况下需要对ziplist执行n次空间重分配操作，而且每次空间重分配的最坏时间复杂度为O(n) ----《Redis设计与实现》
但是出现“连锁更新”的情况并不多见，所以这里基本不会造成性能问题。
篇幅有限这里不能细说连锁更新，感兴趣可以阅读《Redis设计与实现》的相关章节以及ziplist.c里的__ziplistCascadeUpdate()函数。

总结

• ziplist是为节省内存空间而生的。
• ziplist是一个为Redis专门提供的底层数据结构之一，本身可以有序也可以无序。当作为list和hash的底层实现时，节点之间没有顺序；当作为zset的底层实现时，节点之间会按照大小顺序排列。

https://blog.csdn.net/zgaoq/article/details/89710600

跳表（skiplist）的理解

听到跳表（skiplist）这个名字，既然是list，那么应该跟链表有关。
跳表是有序链表，但是我们知道，即使对于排过序的链表，我们对于查找还是需要进行通过链表的指针进行遍历的，时间复杂度很高依然是O(n)，这个显然是不能接受的。是否可以像数组那样，通过二分法进行查找呢，但是由于在内存中的存储的不确定性，不能这做。

但是我们可以结合二分法的思想，没错，跳表就是链表与二分法的结合。
1.链表从头节点到尾节点都是有序的
2.可以进行跳跃查找（形如二分法），降低时间复杂度

一个有序的链表，我们选取它的一半的节点用来建索引，这样如果插入一个节点，我们比较的次数就减少了一半。这种做法，虽然增加了50%的空间，但是性能提高了一倍。如上图。

既然，我们已经提取了一层节点索引，那么，可以在第一层索引上再提取索引。如下图。(二级索引应去掉node2节点)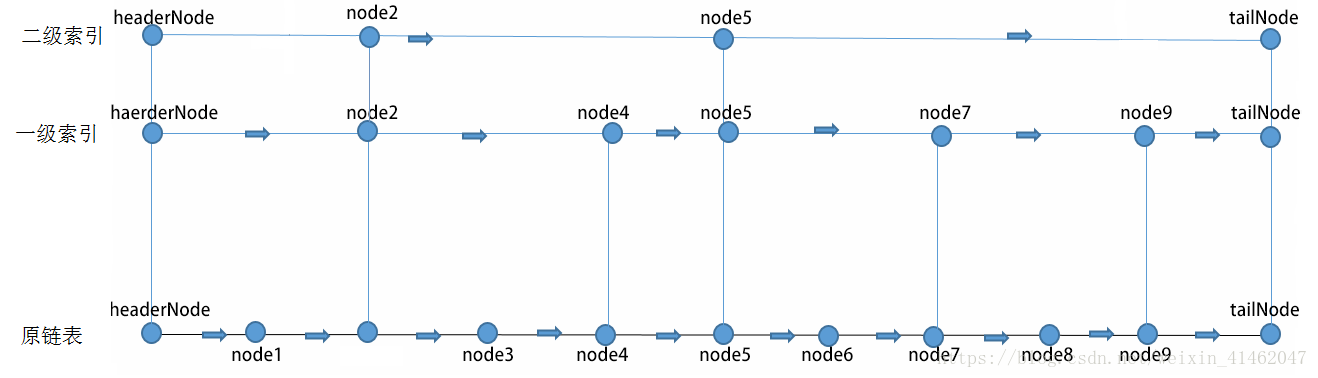

对于node5来说，它的next：

node5->next[2] = tailNode;
node5->next[1] = node7;
node5->next[0] = node6;

• 1
• 2
• 3

对于node7来说，它的next：

node7->next[1] = node9;
node7->next[0] = node8;

• 1
• 2

对于node3来说，它的next：

node3->next[0] = node4;

• 1

查找

如果我们要找node6节点，(二级索引应去掉node2节点)
第一次比较headerNode->next[2]的值，也就是node5的值。显然node5小于node6（跳表的数据是有序的），所以，下一次应该从第2级的node5开始查询，也就是令targetNode = targetNode->next[2];

第二次应该比较node5->next[2]的值，也就是tailNode的值。tailNode的值是最大的。所以结果是大于，下一次应该从第1级的node5开始查询。这里从第2级跳到第1级。但是没有改变targetNode。

第三次我们应该比较node5->next[1]的值，也就是node7的值。因为node7大于node6，所以，下一次应该从第0级的node5开始查询。这里从第1级跳到第0级。也没有改变targetNode。

第四次应该比较node5->next[0]的值，也就是node6的值。这时终于相等，找到了，结束。
如果小于，targetNode往后移，改变targetNode = targetNode->next[0]，如果大于，则没找到，结束。因为这已经是第0级，没法再降了。

综上：
当targetNode->next[i]的值 < 待查找的值时，令targetNode = targetNode->next[i]，targetNode移到第i级的下一个结点；
当targetNode->next[i]的值 > 待查找的值时，向下降级，i- - ，不改变targetNode；
当targetNode->next[i]的值 = 待查找的值时，向下降级，i- - ，不改变targetNode。

最后，再次比较targetNode->next[0]和theElement，判断是否找到。
所以整个运算下来，targetNode是要查找的节点前面那个节点。

插入
当有2级索引时，新的节点先和2级索引比较，再和1级索引比较，最后和原链表比较，最终插到原链表中。当节点很多时，比较次数是原来的四分之一。

当然，当节点足够多的时候，我们还可以继续加索引，保证每一层索引数是低级索引的一半。当这一层只剩两个节点时，就没有必要再建索引了，因为一个节点没有比较的意义。

当很多节点插入时，上层索引节点已经不够用，我们需要在新节点中选取一部分节点提到上一层，跳表的设计者用“抛硬币”的方法选取节点是否提拔，也就是随机的方式，每个节点有50%概率会提拔。这样虽然不会让索引绝对均匀分布，但也会大体上是均匀的。

综上,插入的步骤：

1. 新节点和各层索引节点逐一比较，确定原链表的插入位置。O（logN）
2. 把索引插入到原链表。O（1）
3. 利用抛硬币的随机方式，决定新节点是否提升为上一级索引。结果为“正”则提升并继续抛硬币，结果为“负”则停止。O（logN）

总体上，跳表插入操作的时间复杂度是O（logN），而这种数据结构所占空间是2N，既空间复杂度是 O（N）。

删除

1. 自上而下，查找第一次出现节点的索引，并逐层找到每一层对应的节点。O（logN）
2. 删除每一层查找到的节点，如果该层只剩下1个节点，删除整个一层（原链表除外）。O（logN）

总体上，跳表删除操作的时间复杂度是O（N）。

应用
Redis当中的Sorted-set这种有序的集合，正是对于跳表的改进和应用。

相比于二叉查找树，跳表维持结构平衡的成本比较低，完全靠随机。而二叉查找树需要Rebalance来重新调整平衡的结构。
😃