深入理解浮点数有效位,浮点数分布
平时接触C及Java较多,这种层次的语言对数据的表示有一定局限。基本的数据类型无外呼整数和浮点数。整数好说,一般仅需考虑越界问题。但对于浮点数,除了范围外,通常很容易忽略精度问题。
浮点数为什么会有精度问题?计算机中的浮点数对应于数学当中的小数。简单计算下,32位浮点数最多可以表示2^32个数,但从数学上说区间[0,1]中的小数就有无穷多个。所以计算机是不可能描述得尽的,必然会有一些近似,也就带来了精度损失。
所以在使用计算机中的浮点数之前,我们先要搞清楚计算机表示小数有多准。
浮点数标准
考虑这个问题,首先要知道浮点数在计算机中是怎么表示的。当前,计算机中浮点数采用的是IEEE 754标准。浮点数分为单精度浮点数(32位)和双精度浮点数(64位)。浮点数的基本格式如下:
各部分含义如下:
sign:符号位,0表示正,1表示负
exponent:阶码,浮点数的幂次。一般采用移码表示。
fraction:浮点数的小数部分
上述格式描述的浮点数的十进制值为V=(-1)^SX(1.fraction)X2^E。其中(-1)^S表示符号,1.fraction是二进制的小数,2^E表示幂次,类似于二进制的科学计数法。由于除0外的所有小数都可以写成1.fractionX2^E的形式,因而,在表示浮点数时,省略掉了前面的整数部分1.
对于单精度浮点数,S是1位,E是8位,小数部分是23位。对于双精度浮点数,S是1位,E是11位,小数部分是52位。指数部分E有正负性,使用移码表示。8位E要表示正负,一般减去127,23位则是减去1023。例如,实际的小数指数部分是0的话,在单精度浮点数表示中,E部分是127.
上面描述的是规格化的浮点数,如果浮点数的阶码部分全0或者全1,则表示非规格化的浮点数。
(1)阶码不是全0或全1,规格化浮点数。
(2)阶码全0:表示0.fractionX2^-126次。注意,此时指数部分是1-127.这一类表示了接近0的小数部分。
(3)阶码全1:如果小数部分全0,表示正负无穷大。如果出现1,表示不是一个数(NaN)。
浮点数精度
通过上面的介绍可以发现,浮点数的精度取决于二进制小数部分的精度。对于单精度浮点数,小数部分有23位,对应十进制小数见下表:
| 二进制小数 | 十进制小数 |
| 2^-23 | 0.00000011920928955078125 |
| 2^-22 | 0.0000002384185791015625 |
| 2^-21 | 0.000000476837158203125 |
| 2^-20 | 0.00000095367431640625 |
| 2^-19 | 0.0000019073486328125 |
| 2^-18 | 0.000003814697265625 |
由于是规格化的浮点数,所以小数部分都要加上1,可以知道,单精度浮点数的小数部分最小是1.00000011920928955078125,其次是1.0000002384185791015625,注意到这两个小数之间是有间隔的,如果要表示1.0000001和1.0000002之间的小数,则单精度浮点数无能为力,1.0000001已经是23位小数部分描述的最小值了。通过这样的分析可以发现,23位只能描述到小数点后第7位,即1.0000001,1.0000002,1.0000004,1.0000009对应了二进制的小数值,其他要通过上面几个的组合来表示。
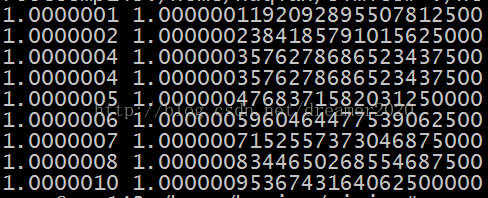
事实上,如果考虑第八位的舍入,1.0000004,1.0000009本身的表示也是不准确的。为了验证这一点,通过程序将1.0000001到1.0000009的结果均打印出来,得如下:
程序中直接将1.0000001到1.0000009分别赋给float型变量,左边一列是输出时小数点后保留7位的结果,右边是保留了25位的结果。
通过上面的结果可以发现,小数点后第7位是部分准确的。例如,1.0000004就是1.00000035通过得到的,其实际保存和1.0000003相同。1.0000006也是通过舍入得到的。再往前第6位及以后均可以通过小数准确表示出来。通常说float数据的有效位是6~7位,也是这个原因。
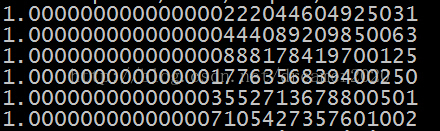
类似的分析,双精度浮点数小数部分有52位,和上面类似,最低6位(2^-52,2^-51,......)表示的规格化小数如下所示。从图中可以看出,双精度浮点数能准确表示到小数点后第15位,第16位部分准确。
整数转化为浮点数
那么如果一个整数用float来存储,保存的精度有多少呢?首先,我们需要将整数转化为二进制科学计数法形式,然后再对应到规格化浮点数中。在处理小数部分时,多余的数位即为损失的精度。
可以测试二进制整数1000 0000 0000 0000 0000 0001,即小数点后面刚好23位。下图展示了小数点后23位、24位及0位的输出结果。只有小数点后24位这一种情况数据表示是不准确的,虽然损失的小数点后第24位,但在科学计数法的前提下,真实值相差为1.
由此可以确定,从1到0xFFFFFF(24位全1,16777215)的整数均可以表示为不超过24位的二进制整数,小数部分不超过23位,因而可以准确的用浮点数表示。还有一部分整数,在表示为二进制的科学计数法时,小数部分不超过23位,也可以准确表示,除此外,其他整数,转化为float后均会损失精度。
一般来说,无论是整数或者小数,用float表示时,从左边第一个非0的数字算起,从高到低的7位是准确的。此后的数位是不能保证精确的。
相应的,从1到0x1FFFFFFFFFFFFF(53位全1,18014398509481983)均可以准确用double来表示。其他整数,只有在转化为double时小数部分不超过52位才可以精确表示。否则,会有一定的精度损失。无论整数或者小数,用double表示时,从左边第一个非0的数字起,从高到低的16位是准确的,此后的数位不一定精确。
浮点数分布
通过上面的分析可以发现,尽管浮点数表示的范围很广,但由于精度损失的存在,加上幂次的放大作用,一个浮点数实际上是表示了周围的一个有理数区间。如果将浮点数绘制到一个数轴上,直观上看,靠近0的部分,浮点数出现较密集。越靠近无穷大,浮点数分布越稀疏,一个浮点值代表了周围一片数据。如下图所示。从这个意义上来说,浮点数不宜直接比较相等,它们是代表了一个数据范围。实际应用中,如果要使用浮点数计算,一定要考虑精度问题。在满足精度要求的前提下,计算结果才是有效的。
在计算精度要求情形下,例如商业计算等,应该避免使用浮点数,严格采取高精度计算。