[C00001F]生活・分个房而已-如何用数学方法合理分配房租/房间？

我和室友们租到了一个非常好的新公寓。但是第一个棘手的问题是，如何合理地分配房间？我们有一个房间非常大，朝西，下午阳光很好；有一个房间稍小，但是房间周正，面街朝东，阳光充足；最后一个房间，面积居中，但是阳光稍有不足。很明显，大家都想要最大的房间。对于另外两个房间，每个人的偏好不一定相同。

作为三个书呆子的（nerdy）经济学家（in training），我们第一反应当然是让价格来决定。但是拍卖有个严重的问题就是，总价无法保证正好等于房租。如果只拍卖其中两个房子，又很难保证无嫉妒（envy-free）。因为第三个房子与另外两个房子并没有差很多，但是拍卖结果很有可能让它变得非常便宜，或者非常贵，这时候一定会有人心理不平衡。举个例子，也许A先生觉得第一间房能带来的效用（utility）是$2000 ，第三间房的效用是$500 。那么拍卖第一间房时，他是愿意出价到$2000 的，然后他拿到这间房。但是等到第二间房也拍卖完以后，大家发现第三间房子只需要支付$100 就可以住了。这时候A先生会后悔，因为他若是住第三间房可以有$400 剩余效用，而住第一间只有$0 的效用。

后来我们发现，哈佛的书呆子（nerdy）数学家们已经想过并解决了相同的问题。解决的方法非常优雅（elegant），并且对个人偏好（preference）只需要三个简单合理的假设便可以证出均衡的存在。

简单概括全文。谈起分配房租，正常人的第一反应是所有人坐下来一起讨论，讨论出一个所有人都认为合理的房租支付方案。此过程分两步，确定房间，确定房租。但是复杂之处在于，不确定房间难以确定房租，不确定房租难以确定房间。因此此文章介绍的方法旨在将这个讨论的过程数学化、定理化，从而实现更高效更准确的分配。纽约时报通过本文介绍这种算法开发了一个分房的 APP（http://www.nytimes.com/interactive/2014/science/rent-division-calculator.html?_r=0%E3%80%82 ）。有兴趣的知友可以去试一试，从而可以更好的理解本文介绍的原理。用两句话概括分房的思路：通过算法产生一个房租分配方式（每一个房间制定一个房价），然后让每一个租客在给定的房价下选择一个最想住的房间。如果有两个人选择了同一个房间，说明该房租分配不合理，换一个分配方式，重复以上步骤，直到找到某一个分配方式使得所有人选择不同的房间。纽约时报的简单介绍（英文） |  http://www.nytimes.com/2014/04/29/science/to-divide-the-rent-start-with-a-triangle.html 。 下文将简要介绍的和谐租房定理证明了，在满足一定条件下，这样的和谐分配方式一定存在。通过对存在性证明的简要介绍，希望读者能大致理解分房算法，以及感受数学的魅力。实际操作可以直接使用 NYT 的 APP，不需要完全理解本文。

和谐租房定理【Rental Harmony Theorem (Su 1999)】. n 个室友想分配 n 个房间。假设以下三个条件成立：

1. 在任何房租分配方式下，每一个人都会接受至少一个房间。

2. 面对一个免费的房间和不免费的房间，每一个人都会选择免费的房间。

3. 偏好集的闭合性（Closed Preference Sets）：如果一个人面对一序列的价格（a sequence of prices），都选择同一个房间，那么面对序列的极限价格（the limiting price），他还会选择同一个房间。

那么， 一定存在一种房租分配方式使得每个人都选择不同的房间。

这个结论是挺令人震撼的。我们不需要知道房间的任何情况，也不需要知道每个人具体的偏好便可以达到理想的无嫉妒（envy-free）均衡。每个人都很满意，因为他要么支付便宜的房租，要么住上了喜欢的房子。定理的前两个假设很实际，我觉得没有太大的争议。1. 毕竟整个房子签下来说明每个人都是想住的。如果有一个人只爱上一个房间并且非它不住，那么不妨就把那个房间定个合理的价钱给他，然后其他人分配剩下的房间。2. 免费的干吗不住。这实际上是对房子的一个要求，保证没有差得离谱的房间（比如没有暖气没有窗户的小冰窖）。这个条件可以放松。3. 闭合性要求，保证人们对房租没有奇怪的偏好。

下面简单讲解一下证明的过程。我们不妨只讨论最简单的三个人情况。我们希望先找到一个分蛋糕问题的解，然后把这个解套用到房租问题上。

事实上，分房问题其实和切蛋糕问题是一样的。 蛋糕问题这里有更多介绍：三个极度自私的人分一个蛋糕，采用什么策略，能让三人都觉得公平？| http://www.zhihu.com/question/20615717 

假设有一个长方形的蛋糕，上面不均匀地分布着不同的装饰配料（toppings），比方说草莓，猕猴桃，樱桃，等等。 每个人在选择的时候既考虑蛋糕的大小，也考虑装饰配料（toppings）。有的人也许很喜欢草莓，所以如果有分到草莓，蛋糕小一点也无所谓。那么这种情况下，如果有三个人，应该怎么分最合理呢？

 

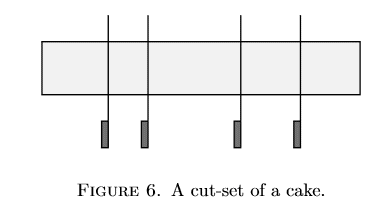
从上面的描述中，我们可以看到其实分房就是在分蛋糕。整个房租是蛋糕，房间的特点就像装饰配料。不同于蛋糕的是，这时候每个都想要最少的房租。我们一会儿说如何转化的问题。

Simmons (1980) 提出一个蛋糕问题的解决方案，利用了 Sperner 引理（Sperner's lemma）。

我们只考虑三个人的情况。取一个大三角形，把大三角形的顶点分别标成 1，2，3。然后它再细分成很多小三角形（elementary triangles） ，如下图所示。之后再给每个小三角形的顶点随机标号。标号遵循一个原则，在大三角形边上的顶点只能出现与该边相连的顶点上的那两个数字。比如，下图中的底边上不能出现 3，但是标 1 或 2 是随机选择的。三角形内部的标号完全随机。

 

Sperner's Lemma for Triangles （Sperner 1928）.任何满足上面叙述要求的标号方式叫作 Sperner 式标识的三角形化（Sperner-labelled triangulation），这样的标号一定包含着奇数个（至少一个）小三角形，使得小三角形的三个顶点标号各不相同。（比如上图中灰色部分）

现在把 Sperner 引理运用到分蛋糕问题中去。假设我们有三个吃货，A ，B ，C 。要切三块蛋糕，分别编号 1，2，3 分给他们。先画一个如下图所示的大三角形，博弈论中管这个叫做单纯形（Simplex），是所有可能的蛋糕分配方式的集合。三角形中任一点代表着一种分配方式，并且任何点的 x , y , z 坐标相加的和都为 1 。比如，某一个点在三角形内，坐标为（1/2 , 1/4 , 1/4）， 它意味着编号为 1 的蛋糕体积为整个的 1/2 ，编号 2 的体积为 1/4 ，编号 3 体积为 1/4 。又比如，左下顶点坐标为（ 1 , 0 , 0 ），意味着 1 号蛋糕分走全部。然后，把每个小三角形的顶点按如图所示方法都标上人名，A ，B ，C ，使得每个小三角形的顶点标号都是ABC。

 

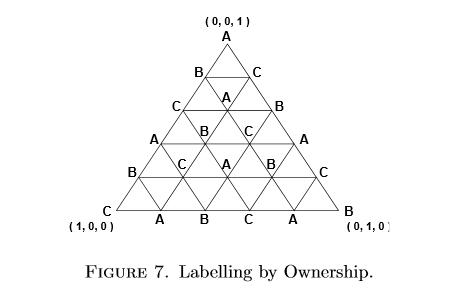
下面精彩的一步要来了。如果我们走遍所有的顶点，问标在顶点的那个人，「如果蛋糕按你所在这一点的方式分配，你会选择哪一块蛋糕？」比如在大三角形的上顶点，分配方式为（ 0 , 0 , 1 ），我们应该问A，「1 号蛋糕和2 号蛋糕只有点渣儿，3 号分走全部蛋糕，你想要哪个？」这时候 A 一定会选 3 。重复上述步骤，我们有可能达到如下图所示的结果。下图中的数字标号有很多很多种可能的方式，下图所示只是其中一种可能性，但是所有可能数字标号都一定满足 Sperner 引理要求的编号方式！（这个结果用到了和谐租房定理的前两个条件）。在实际的算法中，并不需要问遍所有的顶点，详情可以参见论文原文。

 

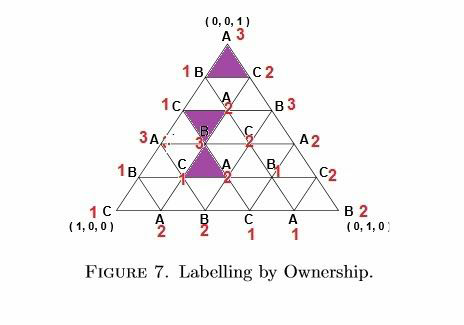
于是通过 Sperner 引理我们知道一定有至少一个小三角形有着三个标号不同的顶点，如图中紫色区域。但是紫色区域依然是一个集合，并不是一个具体的分配方式。如果我们想分的粗糙一点，随便在某一个紫色三角形内选一点 （比如某紫色三角形几何中心）便找到了近似合理的分配方式，然后按三角形顶点的标号分配蛋糕。例如，如果用最下方的紫三角，那么 A 得到 2 号蛋糕，B 得到 3 号，C 得到 1 号。1 , 2 , 3 号蛋糕大小由紫三角形内某一点坐标决定。（注意：这个点只是一个估测值，并不能保证三个人在这一点一定会主动选择方案指定的蛋糕，所以说近似合理）

如果希望更精确，可以给定一个误差，然后选择一个紫色三角形继续细分，并重复之前步骤，最终可以找到一个点（分配方式）使得每个人选择不同的蛋糕，（此处用到了定理的第三个条件）。对于出现多个紫三角的情况，所有这些三角在理论上都是等价的，可以随机选择一个。

蛋糕分完了，我们可以用同样的方式分房。一个小问题是，大家都希望房租越少越好。所以我们要用负数（房租补贴）才能直接运用分蛋糕的方法。用一个具体例子来说，假设房租一个月 3000 刀，那么我们可以先要求每人都交一个较高的房租（只要足够高都可以，比如$1200 ），然后将多出部分作为补贴像蛋糕一样分配（我的例子里$600 的补贴）。

于是我们就花了一下午的时间愉快地分出了房间……

 

All figures are adapted from Su (1999). 

Cover photo credit: Home Designing. http://www.home-designing.com/2014/07/3-bedroom-apartment-house-3d-layout-floor-plans  

Reference:

Simmons, F. W., Private communication to Michael Starbird, 1980.

Sperner, Emanuel. "Neuer Beweis für die Invarianz der Dimensionszahl und des Gebietes." Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg. Vol. 6. No. 1. Springer Berlin/Heidelberg, 1928.

Su, Francis Edward. "Rental harmony: Sperner's lemma in fair division." American Mathematical Monthly (1999): 930-942.

Sun, Albert. "To Divide the Rent, Start With a Triangle." The New York Times. The New York Times, 28 Apr. 2014. Web. 02 June 2015.