机器学习学习笔记（1）——错误率、精度、准确率、召回率、F1度量

本文是我在阅读西瓜书的时候的一些学习笔记和少许理解，更多的我个人觉得算是抛砖引玉吧，如果有误，请麻烦纠正。

顺带说一句，自从看了《西瓜书》，再也不愁出去买到烂瓜了。

本文内容是机器学习算法的性能度量，西瓜书上对性能度量的定义是：衡量模型泛化能力的评价标准。简单来说就是我们要怎样评价这个算法的优劣。

 

目录

• 一、混淆矩阵
• 二、错误率与精度
• • 1. 错误率
  • 2. 精度
• 三、准确率、召回率与F1度量
• • 1. 准确率
  • 2. 召回率
  • 3. F1度量
• 四、参考

 

一、混淆矩阵

混淆矩阵也称误差矩阵，是表示精度评价的一种标准格式，用n行n列的矩阵形式来表示[摘自百度百科]。

我们就借鉴书上的二分类混淆矩阵（如果是n分类，那么就是n×n的矩阵），如图所示：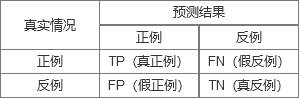

反正就我个人而言，我认为真正例、假正例、假反例、真反例这四个中文是真的难理解，不如从英文的角度来理解这4个定义：

1. 正例：positive，即最后结果是正向的（比如好瓜）；
2. 反例：negative，即最后结果是负向的（比如烂瓜）；
3. TP：True Positive，把正例预测为正例，也就是说，首先预测出来是个正例，其次这是一个真正的正例（比如预测出来是个好瓜，而且是个好瓜）；
4. FP：False Positive，把反例预测为正例，也就是说，首先预测出来是个正例，其次这是个反例（比如预测出来是个好瓜，但是是个烂瓜）；
5. FN：False Negative，把正例预测为反例，也就是说，首先预测出来是个反例，其次这是个正例（比如预测出来是个烂瓜，但是是个好瓜）；
6. TN：True Negative，把反例预测为反例，也就是说，首先预测出来是个反例，其次这是一个真正的反例（比如预测出来是个烂瓜，而且是个烂瓜）。

二、错误率与精度

从上面我们看得出来TP、FP、FN、TN是相互独立的，因为不可能有个瓜预测出来既是好瓜又是烂瓜对吧，所以样本总数 = TP + FP + FN + TN。

1. 错误率

西瓜书上对错误率的定义是：分类错误的样本数占样本总数的比例。

对离散的样例集D，分类错误率为：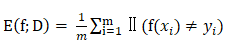

• f(x_i)是指学习器学习示例x_i的结果；
• y_i是指示例x_i的真实标记；
• Ⅱ(f(x_i) ≠ y_i)是指如果f(x_i) = y_i则等于0，否则为1。

而对于连续的数据分布D和概率密度p(·)，错误率为：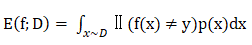

如果我们使用混淆矩阵来描述错误率，那么如下：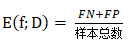

2. 精度

西瓜书上对精度的定义是：分类正确的样本数占样本总数的比例。

对离散的样例集D，分类精度为：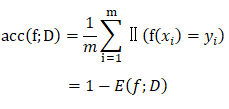

• f(x_i)是指学习器学习示例x_i的结果；
• y_i是指示例x_i的真实标记；
• Ⅱ(f(x_i) = y_i)是指如果f(x_i) = y_i则等于1，否则为0；
• E(f；D)是指错误率。

而对于连续的数据分布D和概率密度p(·)，精度为：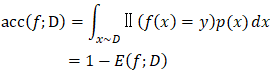

如果我们使用混淆矩阵来描述精度，那么如下：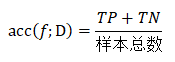

三、准确率、召回率与F1度量

书上更多的是写的“查准率”（precision）和“查全率”（recall），但是我查了些资料，更多的都是写的准确率与召回率，所以我下面都是些准确率和召回率。

由于书上并没有直接给出准确率和召回率的定义，所以我们不妨先看看他们的公式，再来进行理解。

1. 准确率

准确率的公式如下：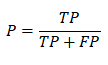

我们不妨把字母代表的意思书写出来，那么这个公式就一目了然了。

那么我们就可以总结出来准确率就是：预测出来为正类中真正的正类所占的比例。

2. 召回率

召回率的公式如下：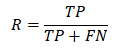

还是一样把字母翻译为汉字：

那么我们就可以总结出来召回率就是：预测出来正确的正类占所有真实正类的比例。

3. F1度量

书上写了这么一句话：查准率（准确率）和查全率（召回率）是一对矛盾的度量。一般来说，查准率（准确率）高时，查全率（召回率）往往偏低；而查全率（召回率）高时，查准率（准确率）往往偏低。

这句话我们结合上样本总数 = TP + FP + FN + TN这个公式来思考，因为在TP相同的情况下，FP高了，那么FN和TN肯定会变小，FN高了，那么FP和TN肯定会变小。

但是我们对一个算法的评估，不可能单单只考虑某一个方面的性能，所以我们需要综合考虑准确率和召回率的性能度量，于是就有了平衡点和F1度量。

平衡点很简单，就是准确率 = 召回率的点，比较这几个点与原点之间的欧氏距离得到的大小，越大的越优。

但是这样又会引出一个问题，比如有的算法更倾向于准确率，有的算法更倾向于召回率（详见书32页例子），那么这么一个简单的考虑方法显然就不适用了，于是就引出了F1度量。

F1度量是基于准确率和召回率的调和平均数的倒数由来的，其原本的公式如下：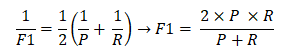

这里先说一下调和平均数，调和平均数就是n个数的倒数的算数平均数，其主要解决的问题如下：

假设你发现脱发严重，你在家门口扫了架自行车飞到了超市买了瓶霸王，然后心满意足慢慢的走回家，求这个过程你的速度的平均数。
首先我们肯定不可能使用算数平均数，因为来回的速度是完全不同的，连近似都不算，几何平均数也不可能，因为我们不是考虑连续乘积的问题，这时就要使用调和平均数。
因为调和平均数有惩罚机制，会更靠近较小值（重视较小值），从上面例子来看，长度一样，前者时间短，速度快，后者时间长，速度慢，那么对于速度的平均数肯定更靠近于小的这个速度，那么取个倒数，大的值就变小，小的值就变大，所以这个就更趋近于我们想要的结果。

而对于我们这个性能度量问题来说，我们肯定是综合考虑准确率和召回率，那么我们引入这样的惩罚机制就不会使得过小的值发不出声音，从而使评估变得更准确。

当然，书上还有F_β这个加权调和平均，主要是能够更好地衡量召回率与准确率的平均值。（我个人认为在实际运用中这个β其实也可以在算法中训练，看算法更倾向于召回率还是准确率）

附：关于F1度量书上公式的推导过程如下：

四、参考

[1]周志华.机器学习[M].清华大学出版社:北京,2016:28.
[2]论智.调和平均数的含义[EB/OL].https://www.zhihu.com/question/23096098/answer/513277869,2018-10-18.

 

机器学习学习笔记（1）——错误率、精度、准确率、召回率、F1度量_机器学习中的错误率-CSDN博客