oom,类加载,红黑树
JVM 发生OOM的四种情况_236004的博客-CSDN博客
1、Java堆溢出:heap
Java堆内存主要用来存放运行过程中所以的对象,该区域OOM异常一般会有如下错误信息;
java.lang.OutofMemoryError:Java heap space
此类错误一般通过Eclipse Memory Analyzer分析OOM时dump的内存快照就能分析出来,到底是由于程序原因导致的内存泄露,还是由于没有估计好JVM内存的大小而导致的内存溢出。
另外,Java堆常用的JVM参数:
-Xms:初始堆大小,默认值为物理内存的1/64(<1GB),默认(MinHeapFreeRatio参数可以调整)空余堆内存小于40%时,JVM就会增大堆直到-Xmx的最大限制.
-Xmx:最大堆大小,默认值为物理内存的1/4(<1GB),默认(MaxHeapFreeRatio参数可以调整)空余堆内存大于70%时,JVM会减少堆直到 -Xms的最小限制
-Xmn:年轻代大小(1.4or lator),此处的大小是(eden + 2 survivor space),与jmap -heap中显示的New gen是不同的。
2、栈溢出:stack
栈用来存储线程的局部变量表、操作数栈、动态链接、方法出口等信息。如果请求栈的深度不足时抛出的错误会包含类似下面的信息:
java.lang.StackOverflowError
另外,由于每个线程占的内存大概为1M,因此线程的创建也需要内存空间。操作系统可用内存-Xmx-MaxPermSize即是栈可用的内存,如果申请创建的线程比较多超过剩余内存的时候,也会抛出如下类似错误:
java.lang.OutofMemoryError: unable to create new native thread
相关的JVM参数有:
-Xss: 每个线程的堆栈大小,JDK5.0以后每个线程堆栈大小为1M,以前每个线程堆栈大小为256K.
在相同物理内存下,减小这个值能生成更多的线程.但是操作系统对一个进程内的线程数还是有限制的,不能无限生成,经验值在3000~5000左右。
3、运行时常量溢出 constant
运行时常量保存在方法区,存放的主要是编译器生成的各种字面量和符号引用,但是运行期间也可能将新的常量放入池中,比如String类的intern方法。
如果该区域OOM,错误结果会包含类似下面的信息:
java.lang.OutofMemoryError: PermGen space
相关的JVM参数有:
-XX:PermSize:设置持久代(perm gen)初始值,默认值为物理内存的1/64
-XX:MaxPermSize:设置持久代最大值,默认为物理内存的1/4
4、方法区溢出 directMemory
方法区主要存储被虚拟机加载的类信息,如类名、访问修饰符、常量池、字段描述、方法描述等。理论上在JVM启动后该区域大小应该比较稳定,但是目前很多框架,比如Spring和Hibernate等在运行过程中都会动态生成类,因此也存在OOM的风险。
如果该区域OOM,错误结果会包含类似下面的信息:
java.lang.OutofMemoryError: PermGen space
相关的JVM参数可以参考运行时常量。
另外,在定位JVM内存问题的时候可以借助于一些辅助信息:
1、日志相关
-XX:+PrintGC:输出形式:
[GC 118250K->113543K(130112K), 0.0094143 secs]
[Full GC 121376K->10414K(130112K), 0.0650971 secs]
-XX:+PrintGCDetails:输出形式:
[GC [DefNew: 8614K->781K(9088K), 0.0123035 secs] 118250K->113543K(130112K), 0.0124633 secs]
[GC [DefNew: 8614K->8614K(9088K), 0.0000665 secs][Tenured: 112761K->10414K(121024K), 0.0433488 secs] 121376K->10414K(130112K), 0.0436268 secs]
-XX:+PrintGCTimeStamps:打印GC停顿耗时
-XX:+PrintGCApplicationStoppedTime:打印垃圾回收期间程序暂停的时间.
-XX:+PrintHeapAtGC:打印GC前后的详细堆栈信息
-Xloggc:filename:把相关日志信息记录到文件以便分析.
2、错误调试相关:
-XX:ErrorFile=./hs_err_pid.log:如果JVM crashed,将错误日志输出到指定文件路径。
-XX:HeapDumpPath=./java_pid.hprof:堆内存快照的存储文件路径。
-XX:-HeapDumpOnOutOfMemoryError:在OOM时,输出一个dump.core文件,记录当时的堆内存快照
3、类装载相关
-XX:-TraceClassLoading:打印class装载信息到stdout。记Loaded状态。
-XX:-TraceClassUnloading:打印class的卸载信息到stdout。记Unloaded状态。
来源:http://www.cnblogs.com/baizhanshi/p/6704731.html
Java 自定义 ClassLoader 实现 JVM 类加载 - 简书 (jianshu.com)
定义需要加载的类
为了能够实现类加载,并展示效果,定义一个Hello类,再为其定义一个sayHello()方法,加载Hello类之后,调用它的sayHello()方法。
public class Hello {
public static void sayHello(){
System.out.println("Hello,I am ....");
}
}定义类加载器
自定义加载器,需要继承ClassLoader,并重写里面的protected Class<?> findClass(String name) throws ClassNotFoundException方法。
import java.io.File;
import java.io.FileInputStream;
import java.io.IOException;
import java.lang.reflect.Method;
import java.nio.MappedByteBuffer;
import java.nio.channels.FileChannel;
import java.nio.channels.FileChannel.MapMode;
public class MyClassLoader extends ClassLoader {
/**
* 重写父类方法,返回一个Class对象
* ClassLoader中对于这个方法的注释是:
* This method should be overridden by class loader implementations
*/
protected Class<?> findClass(String name) throws ClassNotFoundException {
Class clazz = null;
String classFilename = name + ".class";
File classFile = new File(classFilename);
if (classFile.exists()) {
try (FileChannel fileChannel = new FileInputStream(classFile)
.getChannel();) {
MappedByteBuffer mappedByteBuffer = fileChannel
.map(MapMode.READ_ONLY, 0, fileChannel.size());
byte[] b = mappedByteBuffer.array();
clazz = defineClass(name, b, 0, b.length);
} catch (IOException e) {
e.printStackTrace();
}
}
if (clazz == null) {
throw new ClassNotFoundException(name);
}
return clazz;
}
public static void main(String[] args) throws Exception{
MyClassLoader myClassLoader = new MyClassLoader();
Class clazz = myClassLoader.loadClass(args[0]);
Method sayHello = clazz.getMethod("sayHello");
sayHello.invoke(null, null);
}
}编译需要加载的类文件
类加载的时候加载的是字节码文件,所以需要预先把定义的Hello类编译成字节友文件。
javac Hello.java验证字节码文件是否编译成功,利用二进制文件查看器查看我们编译之后的文件,样式如下:
0000000 177312 137272 000000 032000 016000 000012 000006 004416
0000020 007400 010000 000010 005021 011000 011400 000007 003424
0000040 012400 000001 036006 067151 072151 000476 001400 024450
0000060 000526 002000 067503 062544 000001 046017 067151 047145
0000100 066565 062542 052162 061141 062554 000001 071410 074541
0000120 062510 066154 000557 005000 067523 071165 062543 064506
0000140 062554 000001 044012 066145 067554 065056 073141 006141
0000160 003400 004000 000007 006026 013400 014000 000001 044017
0000200 066145 067554 044454 060440 020155 027056 027056 000007
0000220 006031 015000 015400 000001 044005 066145 067554 000001
0000240 065020 073141 027541 060554 063556 047457 065142 061545
0000260 000564 010000 060552 060566 066057 067141 027547 074523
0000300 072163 066545 000001 067403 072165 000001 046025 060552
0000320 060566 064457 027557 071120 067151 051564 071164 060545
0000340 035555 000001 065023 073141 027541 067551 050057 064562
0000360 072156 072123 062562 066541 000001 070007 064562 072156
0000400 067154 000001 024025 065114 073141 027541 060554 063556
0000420 051457 071164 067151 035547 053051 020400 002400 003000
0000440 000000 000000 001000 000400 003400 004000 000400 004400
0000460 000000 016400 000400 000400 000000 002400 133452 000400
0000500 000261 000000 000001 000012 000000 000006 000001 000000
0000520 000002 000011 000013 000010 000001 000011 000000 000045
0000540 000002 000000 000000 131011 001000 001422 000266 130404
0000560 000000 000400 005000 000000 005000 001000 000000 002000
0000600 004000 002400 000400 006000 000000 001000 006400
0000616b树和b+树的区别
转载自https://blog.csdn.net/login_sonata/article/details/75268075
一,b树
b树(balance tree)和b+树应用在数据库索引,可以认为是m叉的多路平衡查找树,但是从理论上讲,二叉树查找速度和比较次数都是最小的,为什么不用二叉树呢?
因为我们要考虑磁盘IO的影响,它相对于内存来说是很慢的。数据库索引是存储在磁盘上的,当数据量大时,就不能把整个索引全部加载到内存了,只能逐一加载每一个磁盘页(对应索引树的节点)。所以我们要减少IO次数,对于树来说,IO次数就是树的高度,而“矮胖”就是b树的特征之一,它的每个节点最多包含m个孩子,m称为b树的阶,m的大小取决于磁盘页的大小。
█一个M阶的b树具有如下几个特征:
- 定义任意非叶子结点最多只有M个儿子,且M>2;
- 根结点的儿子数为[2, M];
- 除根结点以外的非叶子结点的儿子数为[M/2, M],向上取整;
- 非叶子结点的关键字个数=儿子数-1;
- 所有叶子结点位于同一层;
- k个关键字把节点拆成k+1段,分别指向k+1个儿子,同时满足查找树的大小关系。
█有关b树的一些特性,注意与后面的b+树区分:
- 关键字集合分布在整颗树中;
- 任何一个关键字出现且只出现在一个结点中;
- 搜索有可能在非叶子结点结束;
- 其搜索性能等价于在关键字全集内做一次二分查找;
█如图是一个3阶b树,顺便讲一下查询元素5的过程: 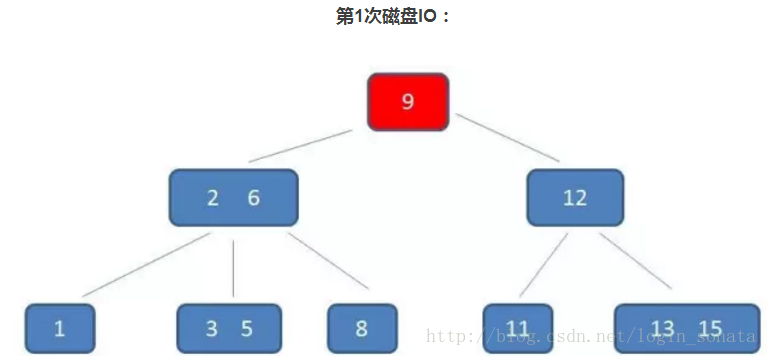
1,第一次磁盘IO,把9所在节点读到内存,把目标数5和9比较,小,找小于9对应的节点;
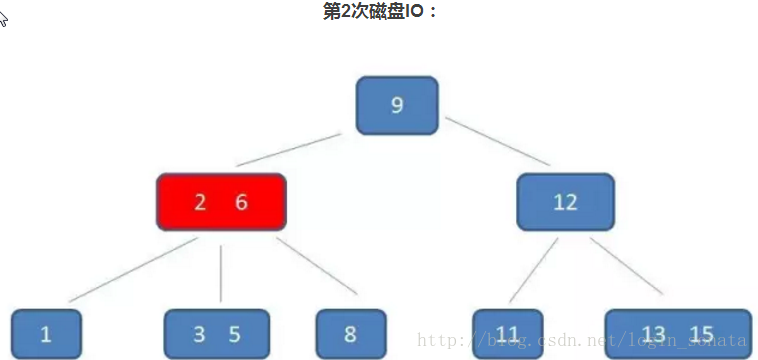
2,第二次磁盘IO,还是读节点到内存,在内存中把5依次和2、6比较,定位到2、6中间区域对应的节点;
3,第三次磁盘IO就不上图了,跟第二步一样,然后就找到了目标5。
可以看到,b树在查询时的比较次数并不比二叉树少,尤其是节点中的数非常多时,但是内存的比较速度非常快,耗时可以忽略,所以只要树的高度低,IO少,就可以提高查询性能,这是b树的优势之一。
█b树的插入删除元素操作:
比如我们要在下图中插入元素4: 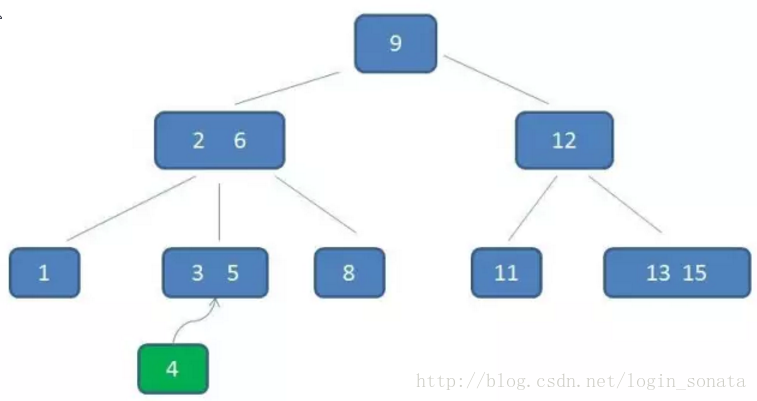
1,首先自顶向下查询找到4应该在的位置,即3、5之间;
2,但是3阶b树的节点最多只能有2个元素,所以把3、4、5里面的中间元素4上移(中间元素上移是插入操作的关键);
3,上一层节点加入4之后也超载了,继续中间元素上移的操作,现在根节点变成了4、9;
4,还要满足查找树的性质,所以对元素进行调整以满足大小关系,始终维持多路平衡也是b树的优势,最后变成这样: 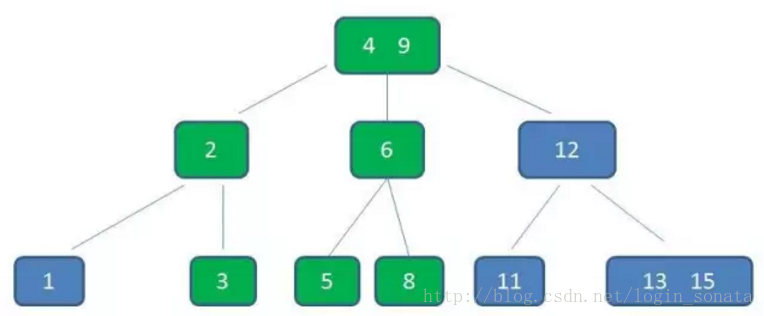
再比如我们要删除元素11:
1,自顶向下查询到11,删掉它;
2,然后不满足b树的条件了,因为元素12所在的节点只有一个孩子了,所以我们要“左旋”,元素12下来,元素13上去: 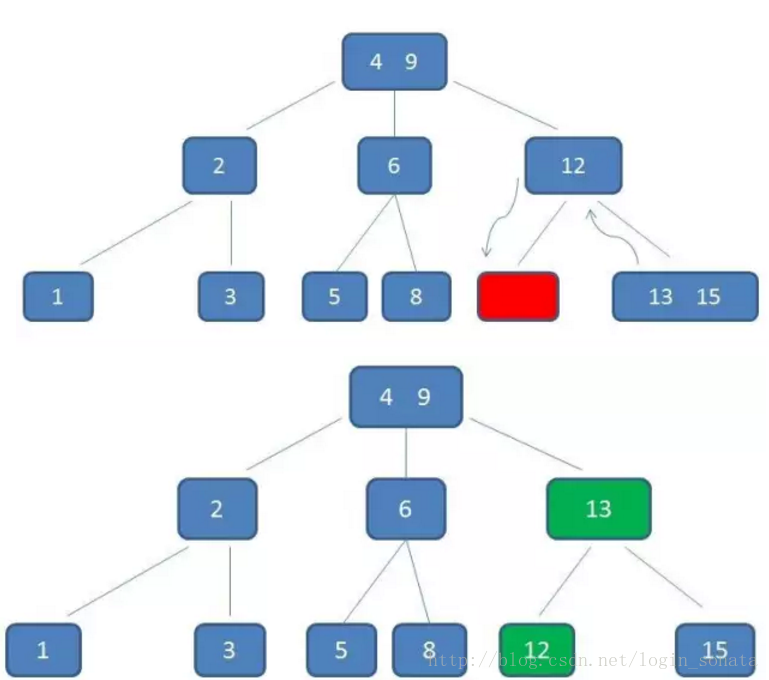
这时如果再删除15呢?很简单,当元素个数太少以至于不能再旋转时,12直接上去就行了。
二,b+树
b+树,是b树的一种变体,查询性能更好。m阶的b+树的特征:
- 有n棵子树的非叶子结点中含有n个关键字(b树是n-1个),这些关键字不保存数据,只用来索引,所有数据都保存在叶子节点(b树是每个关键字都保存数据)。
- 所有的叶子结点中包含了全部关键字的信息,及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
- 所有的非叶子结点可以看成是索引部分,结点中仅含其子树中的最大(或最小)关键字。
- 通常在b+树上有两个头指针,一个指向根结点,一个指向关键字最小的叶子结点。
- 同一个数字会在不同节点中重复出现,根节点的最大元素就是b+树的最大元素。
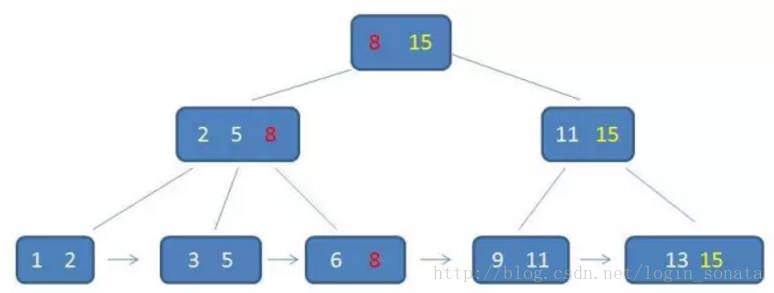
█b+树相比于b树的查询优势:
- b+树的中间节点不保存数据,所以磁盘页能容纳更多节点元素,更“矮胖”;
- b+树查询必须查找到叶子节点,b树只要匹配到即可不用管元素位置,因此b+树查找更稳定(并不慢);
- 对于范围查找来说,b+树只需遍历叶子节点链表即可,b树却需要重复地中序遍历,如下两图:
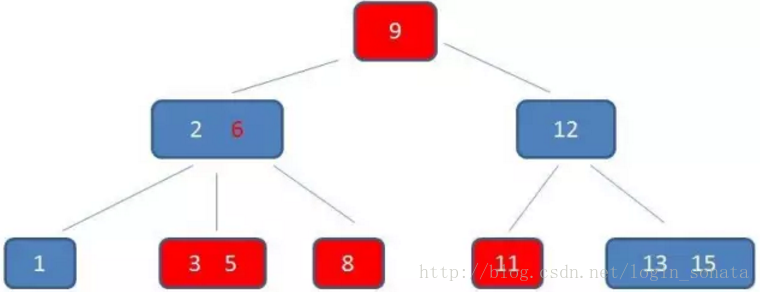
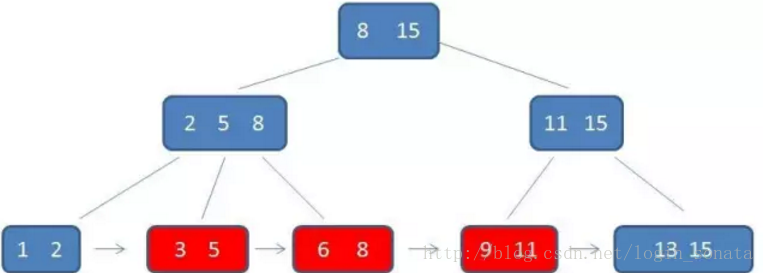




————————————








————————————



二叉查找树(BST)具备什么特性呢?
1.左子树上所有结点的值均小于或等于它的根结点的值。
2.右子树上所有结点的值均大于或等于它的根结点的值。
3.左、右子树也分别为二叉排序树。
下图中这棵树,就是一颗典型的二叉查找树:


1.查看根节点9:

2.由于10 > 9,因此查看右孩子13:

3.由于10 < 13,因此查看左孩子11:
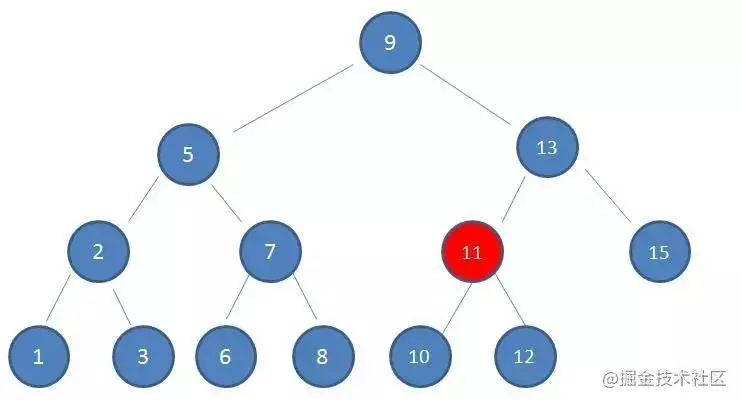
4.由于10 < 11,因此查看左孩子10,发现10正是要查找的节点:
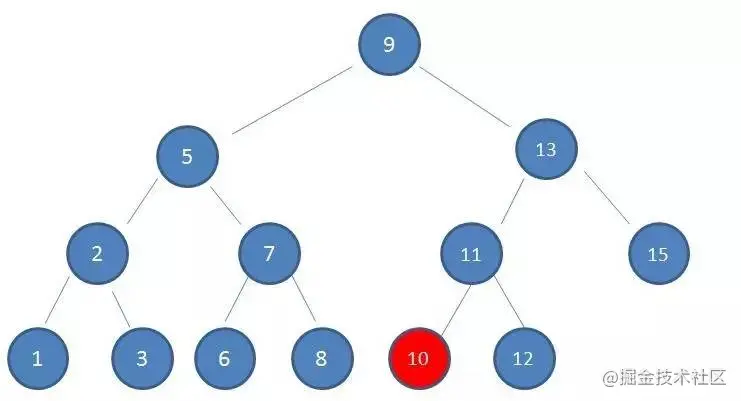






假设初始的二叉查找树只有三个节点,根节点值为9,左孩子值为8,右孩子值为12:
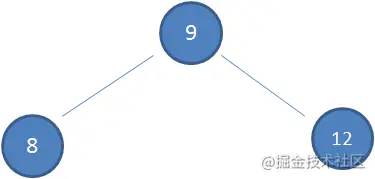
接下来我们依次插入如下五个节点:7,6,5,4,3。依照二叉查找树的特性,结果会变成什么样呢?
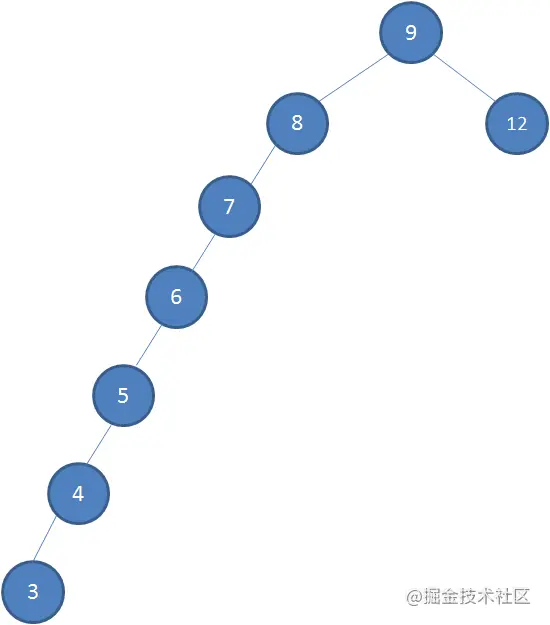




1.节点是红色或黑色。
2.根节点是黑色。
3.每个叶子节点都是黑色的空节点(NIL节点)。
4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
下图中这棵树,就是一颗典型的红黑树:




什么情况下会破坏红黑树的规则,什么情况下不会破坏规则呢?我们举两个简单的栗子:
1.向原红黑树插入值为14的新节点:
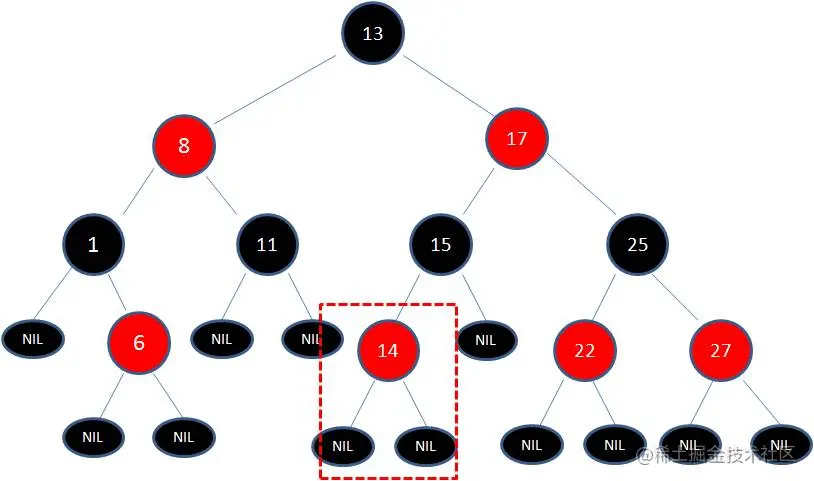
由于父节点15是黑色节点,因此这种情况并不会破坏红黑树的规则,无需做任何调整。
2.向原红黑树插入值为21的新节点:
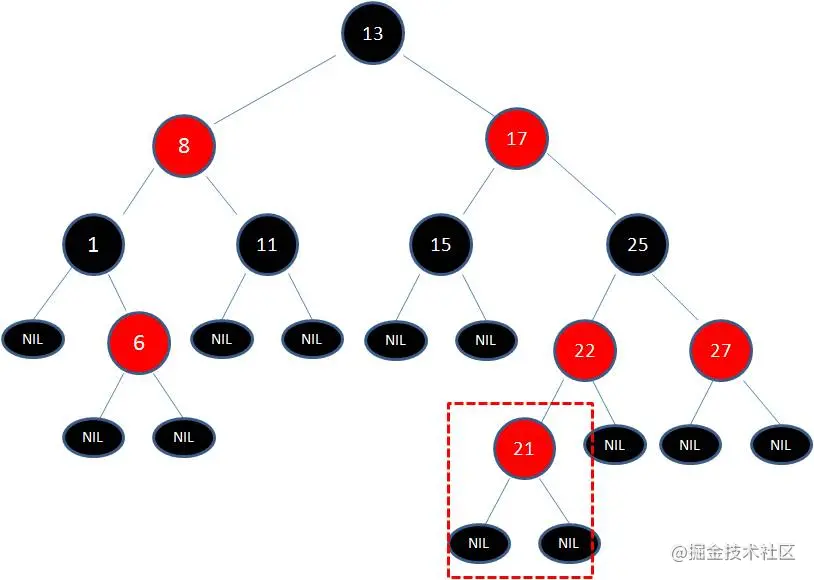
由于父节点22是红色节点,因此这种情况打破了红黑树的规则4(每个红色节点的两个子节点都是黑色),必须进行调整,使之重新符合红黑树的规则。


变色:
为了重新符合红黑树的规则,尝试把红色节点变为黑色,或者把黑色节点变为红色。
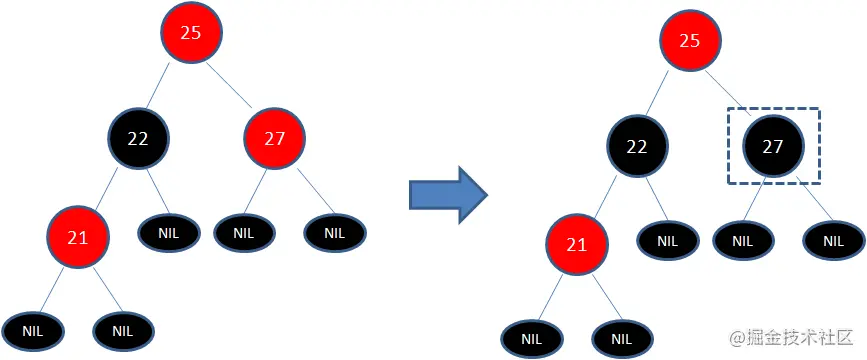
下图所表示的是红黑树的一部分,需要注意节点25并非根节点。因为节点21和节点22连续出现了红色,不符合规则4,所以把节点22从红色变成黑色:
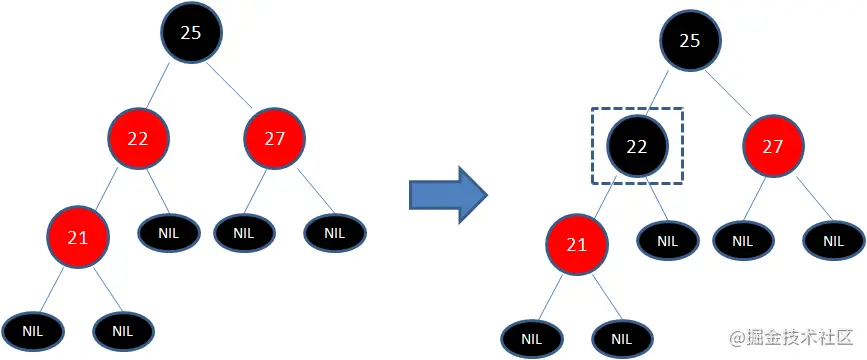
但这样并不算完,因为凭空多出的黑色节点打破了规则5,所以发生连锁反应,需要继续把节点25从黑色变成红色:
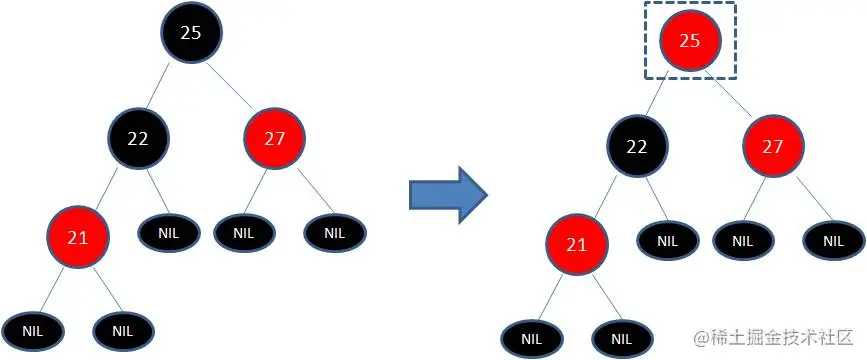
此时仍然没有结束,因为节点25和节点27又形成了两个连续的红色节点,需要继续把节点27从红色变成黑色:
左旋转:
逆时针旋转红黑树的两个节点,使得父节点被自己的右孩子取代,而自己成为自己的左孩子。说起来很怪异,大家看下图:
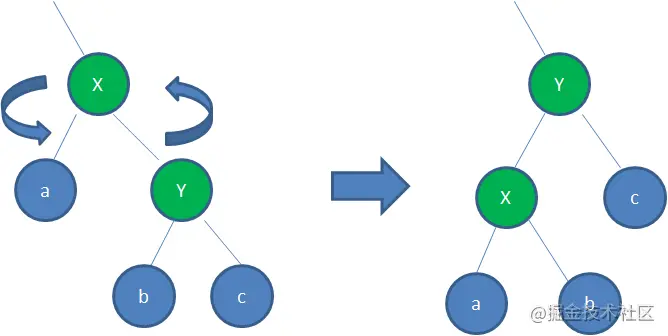
图中,身为右孩子的Y取代了X的位置,而X变成了自己的左孩子。此为左旋转。
右旋转:
顺时针旋转红黑树的两个节点,使得父节点被自己的左孩子取代,而自己成为自己的右孩子。大家看下图:

图中,身为左孩子的Y取代了X的位置,而X变成了自己的右孩子。此为右旋转。


我们以刚才插入节点21的情况为例:

首先,我们需要做的是变色,把节点25及其下方的节点变色:
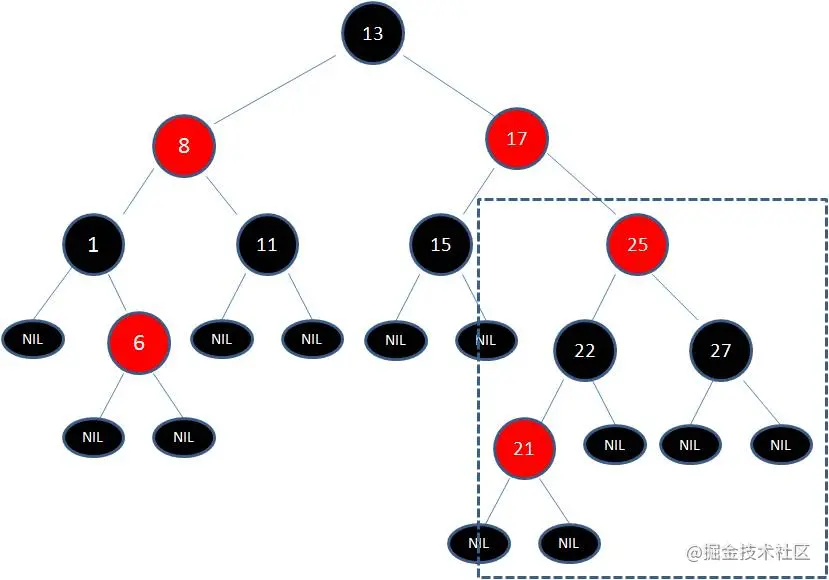
此时节点17和节点25是连续的两个红色节点,那么把节点17变成黑色节点?恐怕不合适。这样一来不但打破了规则4,而且根据规则2(根节点是黑色),也不可能把节点13变成红色节点。
变色已无法解决问题,我们把节点13看做X,把节点17看做Y,像刚才的示意图那样进行左旋转:


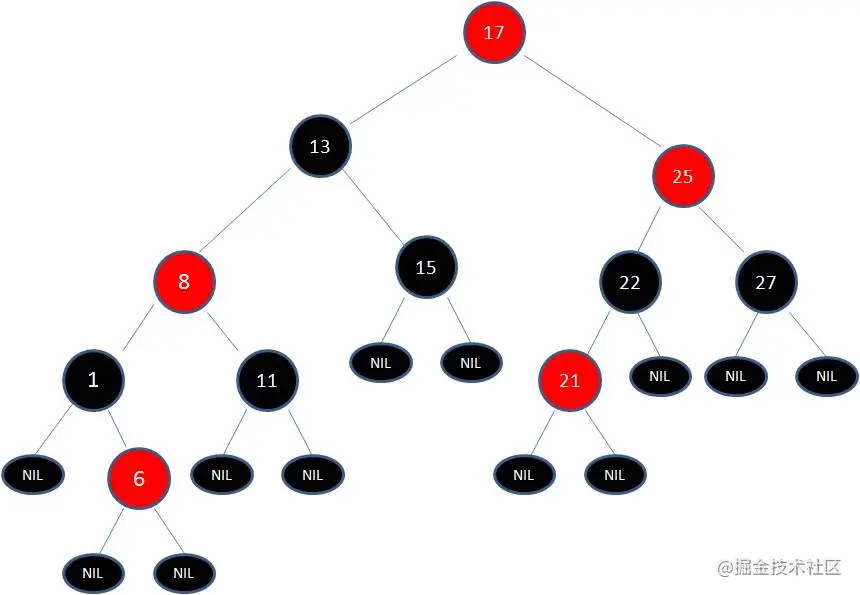
由于根节点必须是黑色节点,所以需要变色,变色结果如下:
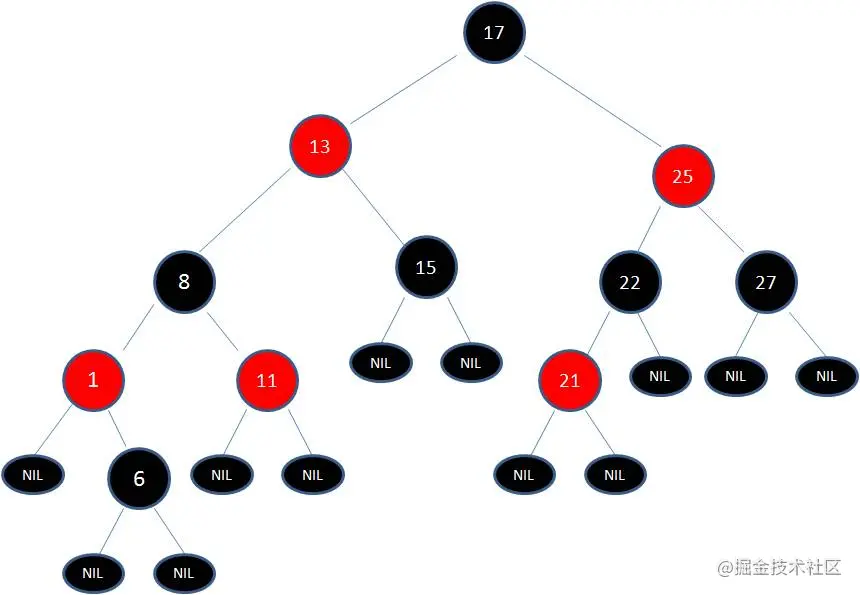
这样就结束了吗?并没有。因为其中两条路径(17 -> 8 -> 6 -> NIL)的黑色节点个数是4,其他路径的黑色节点个数是3,不符合规则5。
这时候我们需要把节点13看做X,节点8看做Y,像刚才的示意图那样进行右旋转:

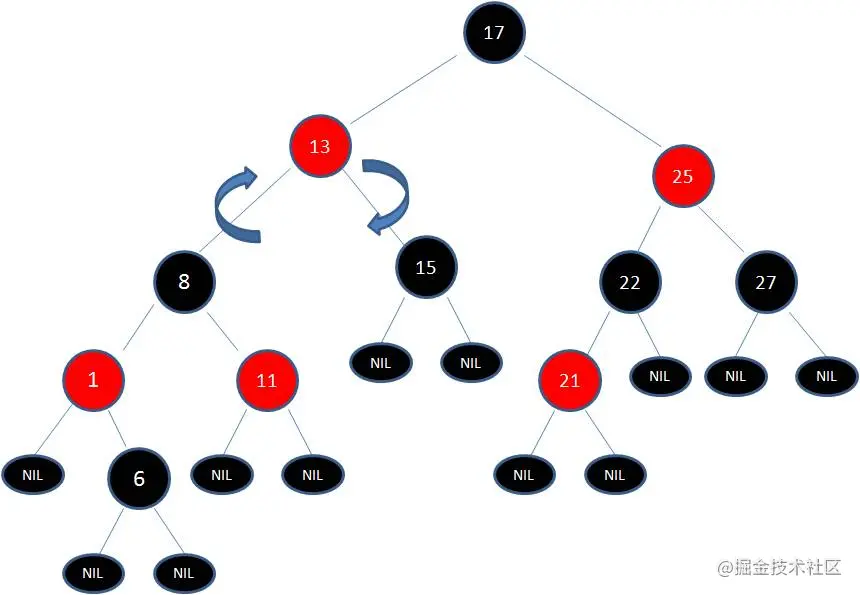

最后根据规则来进行变色:
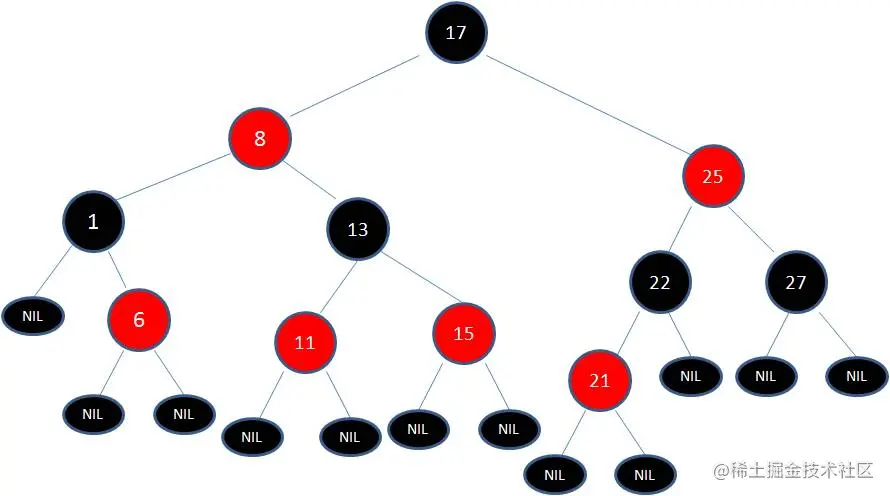
如此一来,我们的红黑树变得重新符合规则。这一个例子的调整过程比较复杂,经历了如下步骤:
变色 -> 左旋转 -> 变色 -> 右旋转 -> 变色




几点说明:
1. 关于红黑树自平衡的调整,插入和删除节点的时候都涉及到很多种Case,由于篇幅原因无法展开来一一列举,有兴趣的朋友可以参考维基百科,里面讲的非常清晰。
2.漫画中红黑树调整过程的示例是一种比较复杂的情形,没太看明白的小伙伴也不必钻牛角尖,关键要懂得红黑树自平衡调整的主体思想。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号