图解Gossip：可能是最有趣的一致性协议

Gossip是什么

Gossip协议是一个通信协议，一种传播消息的方式，灵感来自于：瘟疫、社交网络等。使用Gossip协议的有：Redis Cluster、Consul、Apache Cassandra等。

六度分隔理论

说到社交网络，就不得不提著名的六度分隔理论。1967年，哈佛大学的心理学教授Stanley Milgram想要描绘一个连结人与社区的人际连系网。做过一次连锁信实验，结果发现了“六度分隔”现象。简单地说：“你和任何一个陌生人之间所间隔的人不会超过六个，也就是说，最多通过六个人你就能够认识任何一个陌生人。

数学解释该理论：若每个人平均认识260人，其六度就是260↑6 =1,188,137,600,000。消除一些节点重复，那也几乎覆盖了整个地球人口若干多多倍，这也是Gossip协议的雏形。

原理

Gossip协议基本思想就是：一个节点想要分享一些信息给网络中的其他的一些节点。于是，它周期性的随机选择一些节点，并把信息传递给这些节点。这些收到信息的节点接下来会做同样的事情，即把这些信息传递给其他一些随机选择的节点。一般而言，信息会周期性的传递给N个目标节点，而不只是一个。这个N被称为fanout（这个单词的本意是扇出）。

用途

Gossip协议的主要用途就是信息传播和扩散：即把一些发生的事件传播到全世界。它们也被用于数据库复制，信息扩散，集群成员身份确认，故障探测等。

基于Gossip协议的一些有名的系统：Apache Cassandra，Redis（Cluster模式），Consul等。

图解

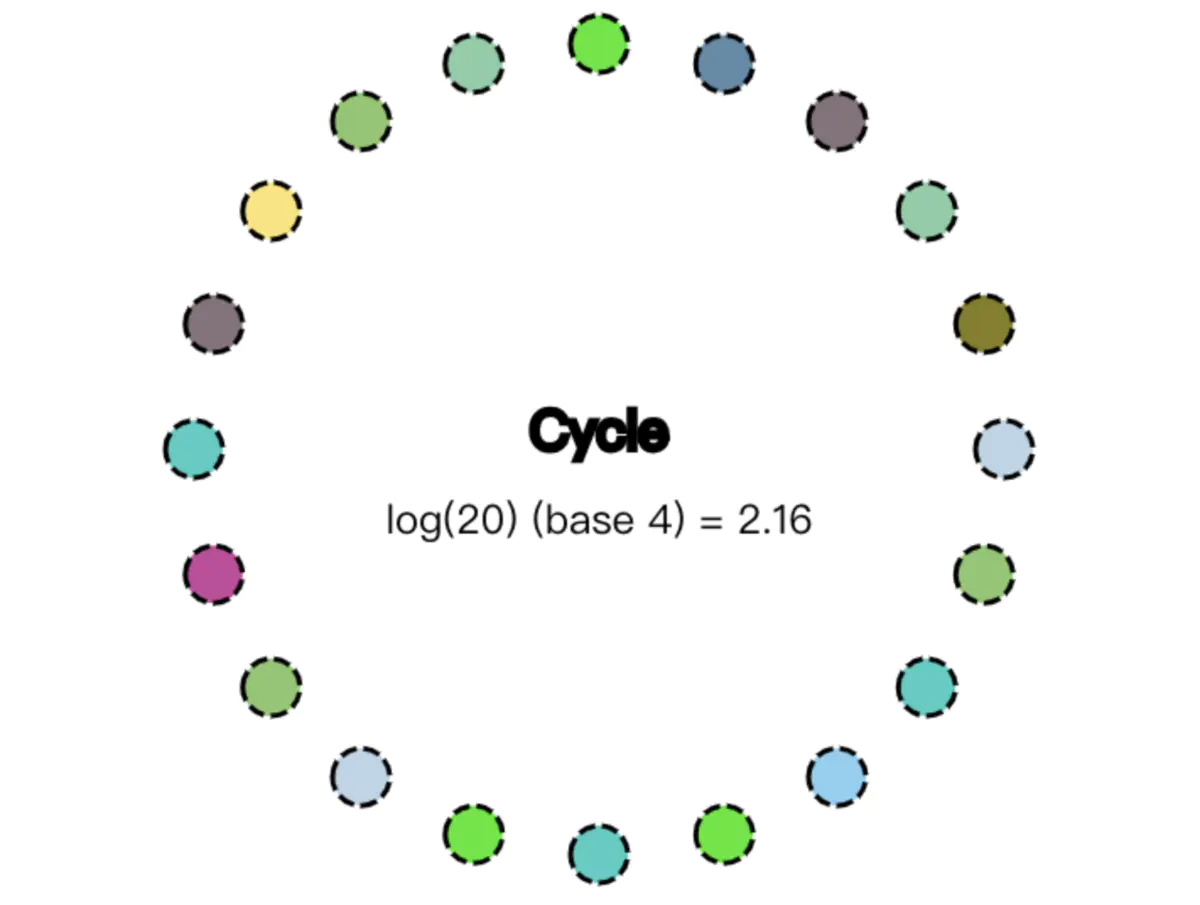
接下来通过多张图片剖析Gossip协议是如何运行的。如下图所示，Gossip协议是周期循环执行的。图中的公式表示Gossip协议把信息传播到每一个节点需要多少次循环动作，需要说明的是，公式中的20表示整个集群有20个节点，4表示某个节点会向4个目标节点传播消息：

 

 

Gossip Protocol

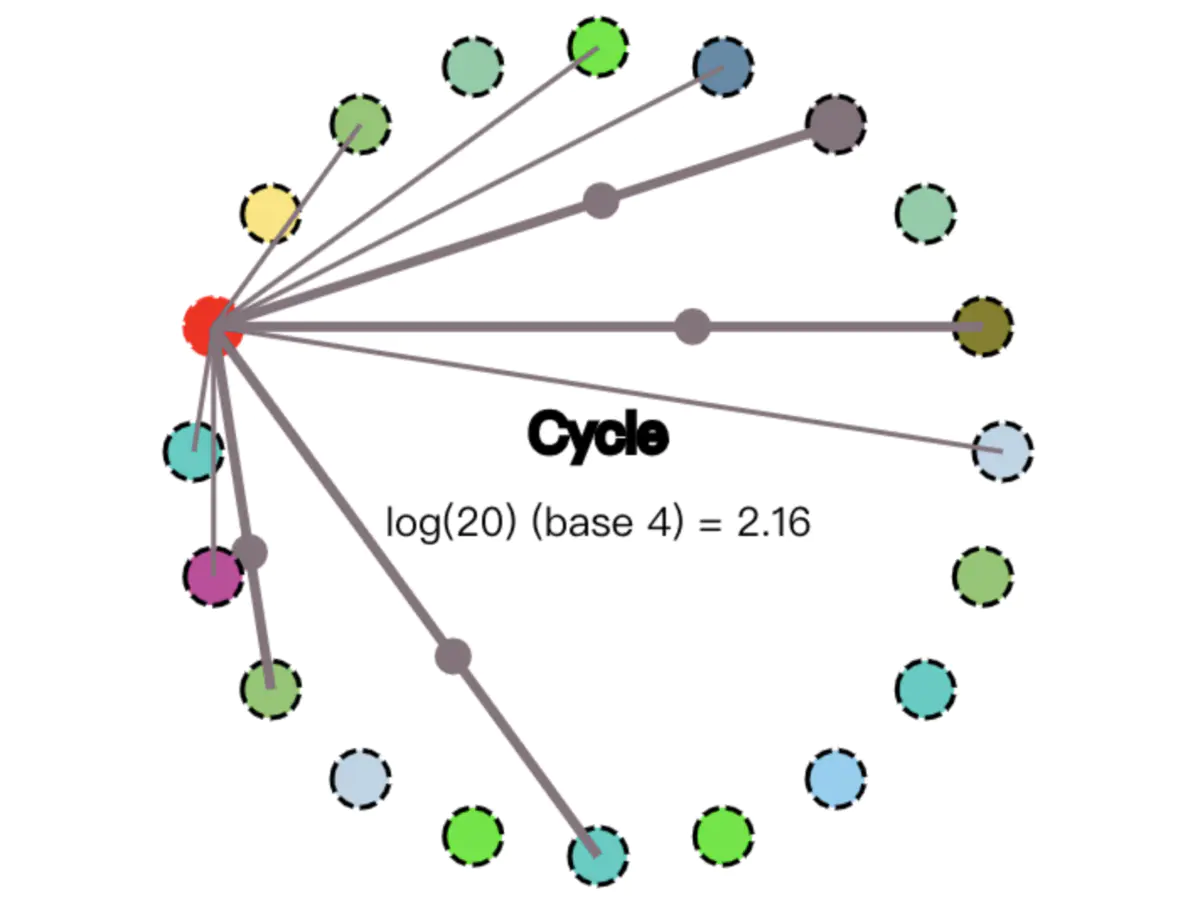
如下图所示，红色的节点表示其已经“受到感染”，即接下来要传播信息的源头，连线表示这个初始化感染的节点能正常连接的节点（其不能连接的节点只能靠接下来感染的节点向其传播消息）。并且N等于4，我们假设4根较粗的线路，就是它第一次传播消息的线路：

 

 

first infected node

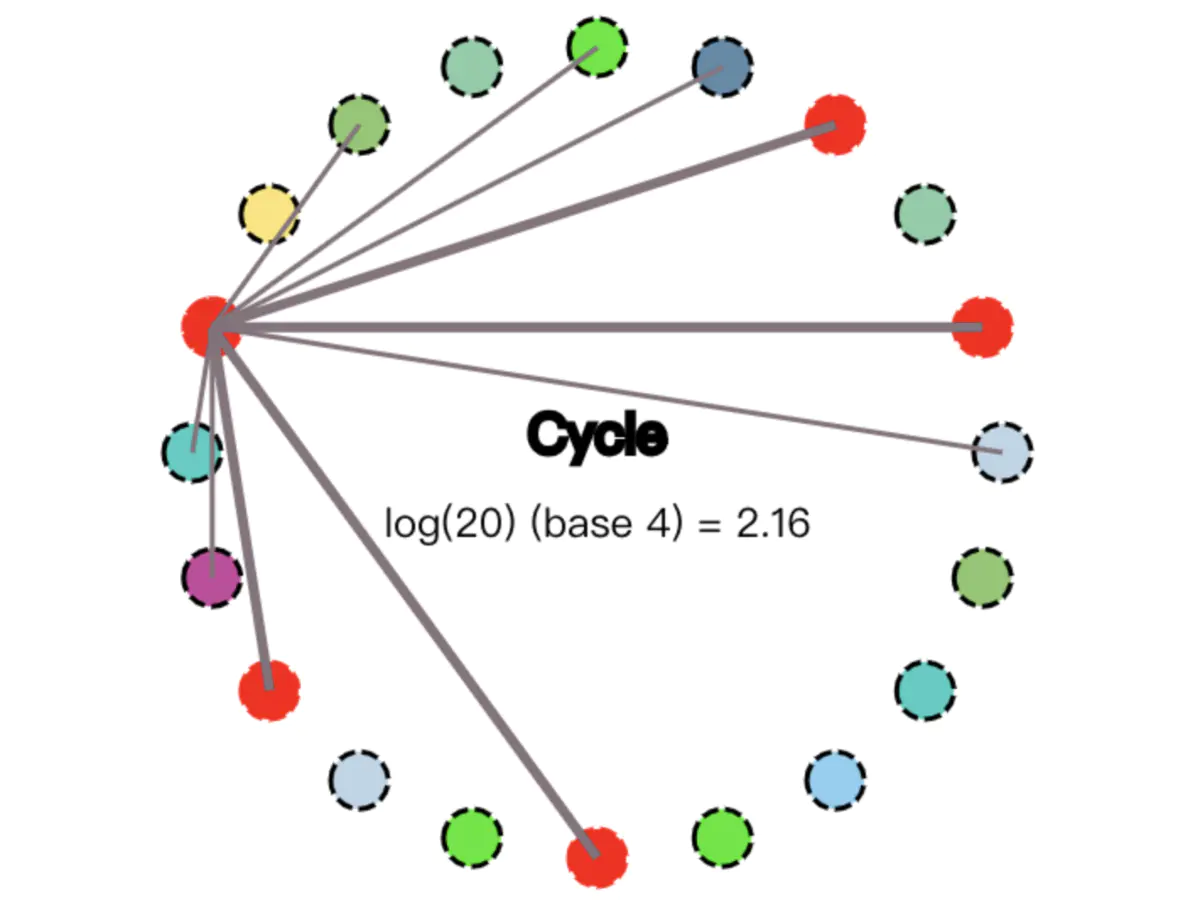
第一次消息完成传播后，新增了4个节点会被“感染”，即这4个节点也收到了消息。这时候，总计有5个节点变成红色：

 

 

infected nodes

那么在下一次传播周期时，总计有5个节点，且这5个节点每个节点都会向4个节点传播消息。最后，经过3次循环，20个节点全部被感染（都变成红色节点），即说明需要传播的消息已经传播给了所有节点：

 

 

infected all nodes

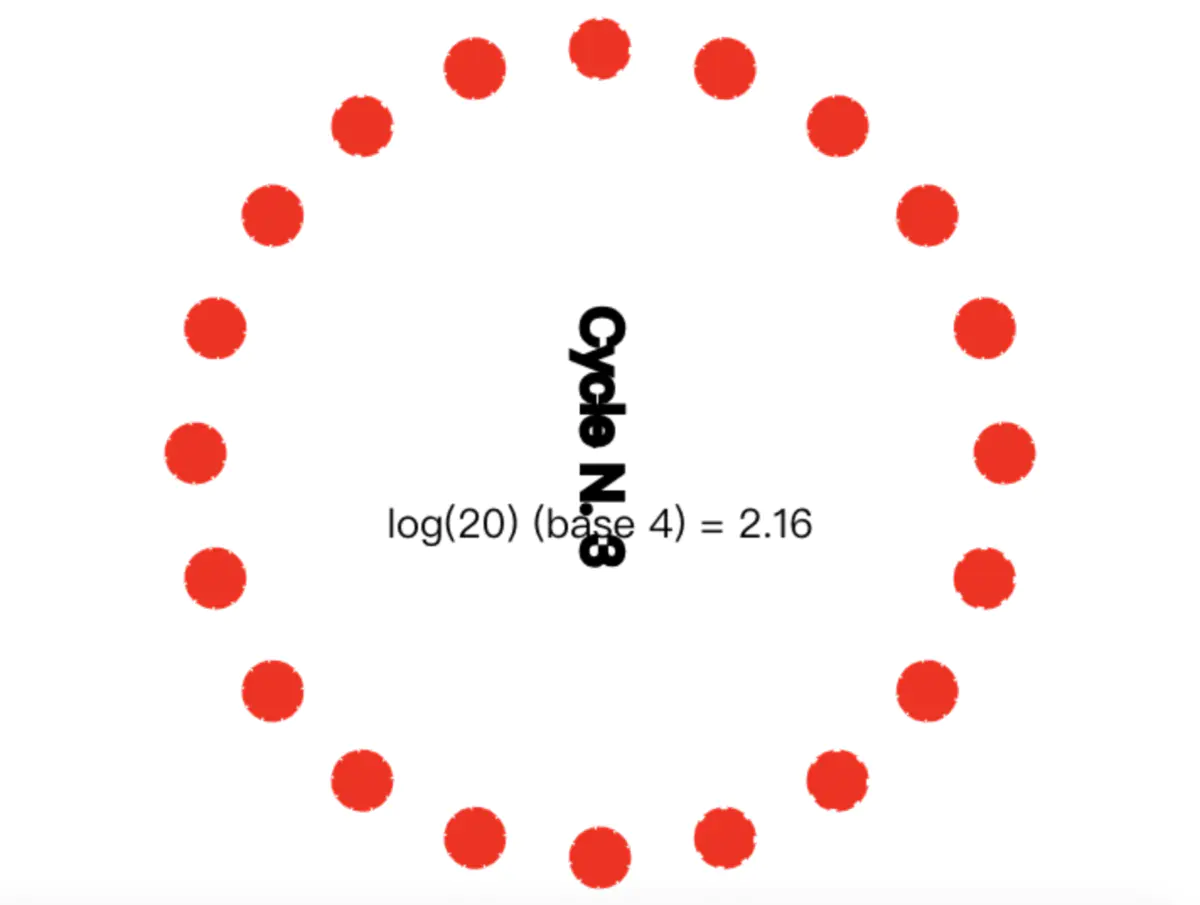
需要说明的是，20个节点且设置fanout=4，公式结果是2.16，这只是个近似值。真实传递时，可能需要3次甚至4次循环才能让所有节点收到消息。这是因为每个节点在传播消息的时候，是随机选择N个节点的，这样的话，就有可能某个节点会被选中2次甚至更多次。

发送消息

由前面对Gossip协议图解分析可知，节点传播消息是周期性的，并且每个节点有它自己的周期。另外，节点发送消息时的目标节点数由参数fanout决定。至于往哪些目标节点发送，则是随机的。

一旦消息被发送到目标节点，那么目标节点也会被感染。一旦某个节点被感染，那么它也会向其他节点传播消息，试图感染更多的节点。最终，每一个节点都会被感染，即消息被同步给了所有节点：

 

 

infected

可扩展性

Gossip协议是可扩展的，因为它只需要O(logN) 个周期就能把消息传播给所有节点。某个节点在往固定数量节点传播消息过程中，并不需要等待确认（ack），并且，即使某条消息传播过程中丢失，它也不需要做任何补偿措施。大哥比方，某个节点本来需要将消息传播给4个节点，但是由于网络或者其他原因，只有3个消息接收到消息，即使这样，这对最终所有节点接收到消息是没有任何影响的。

如下表格所示，假定fanout=4，那么在节点数分别是20、40、80、160时，消息传播到所有节点需要的循环次数对比，在节点成倍扩大的情况下，循环次数并没有增加很多。所以，Gossip协议具备可扩展性：

 

可扩展性

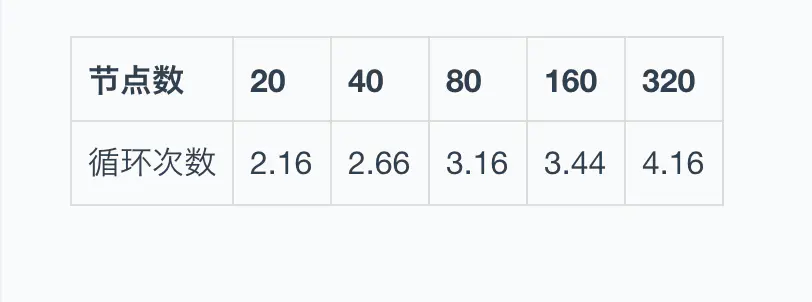
失败容错

Gossip也具备失败容错的能力，即使网络故障等一些问题，Gossip协议依然能很好的运行。因为一个节点会多次分享某个需要传播的信息，即使不能连通某个节点，其他被感染的节点也会尝试向这个节点传播信息。

健壮性

Gossip协议下，没有任何扮演特殊角色的节点（比如leader等）。任何一个节点无论什么时候下线或者加入，并不会破坏整个系统的服务质量。

然而，Gossip协议也有不完美的地方，例如，拜占庭问题（Byzantine）。即，如果有一个恶意传播消息的节点，Gossip协议的分布式系统就会出问题。

https://zhuanlan.zhihu.com/p/41228196

背景

Gossip protocol 也叫 Epidemic Protocol （流行病协议），实际上它还有很多别名，比如：“流言算法”、“疫情传播算法”等。

 

这个协议的作用就像其名字表示的意思一样，非常容易理解，它的方式其实在我们日常生活中也很常见，比如电脑病毒的传播，森林大火，细胞扩散等等。

 

Gossip protocol 最早是在 1987 年发表在 ACM 上的论文 《Epidemic Algorithms for Replicated Database Maintenance》中被提出。主要用在分布式数据库系统中各个副本节点同步数据之用，这种场景的一个最大特点就是组成的网络的节点都是对等节点，是非结构化网络，这区别与之前介绍的用于结构化网络中的 DHT 算法 Kadmelia。

 

我们知道，很多知名的 P2P 网络或区块链项目，比如 IPFS，Ethereum 等，都使用了 Kadmelia 算法，而大名鼎鼎的 Bitcoin 则是使用了 Gossip 协议来传播交易和区块信息。

实际上，只要仔细分析一下场景就知道，Ethereum 使用 DHT 算法并不是很合理，因为它使用节点保存整个链数据，不像 IPFS 那样分片保存数据，因此 Ethereum 真正适合的协议应该像 Bitcoin 那样，是 Gossip 协议。

 

这里先简单介绍一下 Gossip 协议的执行过程：

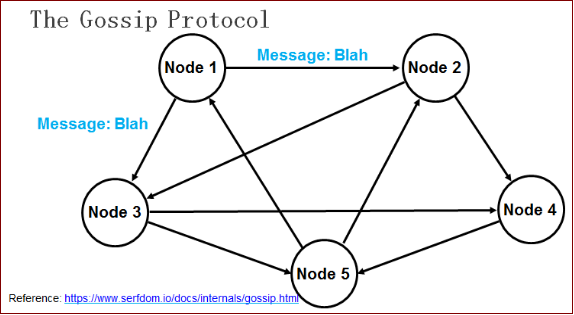
Gossip 过程是由种子节点发起，当一个种子节点有状态需要更新到网络中的其他节点时，它会随机的选择周围几个节点散播消息，收到消息的节点也会重复该过程，直至最终网络中所有的节点都收到了消息。这个过程可能需要一定的时间，由于不能保证某个时刻所有节点都收到消息，但是理论上最终所有节点都会收到消息，因此它是一个最终一致性协议。

 

Gossip 演示

现在，我们通过一个具体的实例来深入体会一下 Gossip 传播的完整过程

 

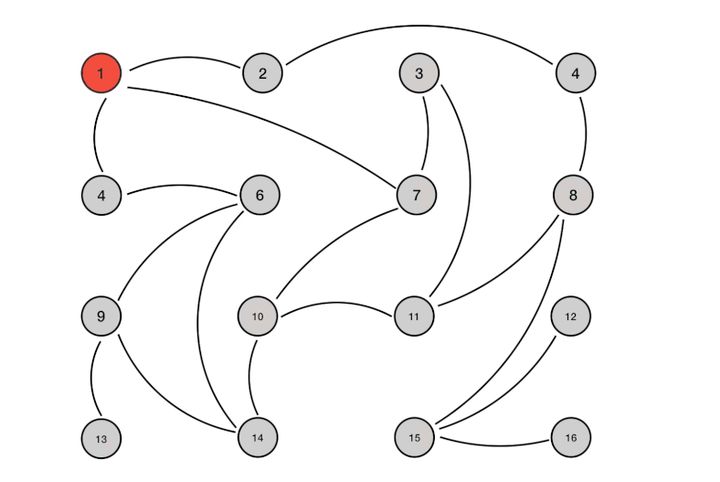
为了表述清楚，我们先做一些前提设定

1、Gossip 是周期性的散播消息，把周期限定为 1 秒

2、被感染节点随机选择 k 个邻接节点（fan-out）散播消息，这里把 fan-out 设置为 3，每次最多往 3 个节点散播。

3、每次散播消息都选择尚未发送过的节点进行散播

4、收到消息的节点不再往发送节点散播，比如 A -> B，那么 B 进行散播的时候，不再发给 A。

注意：Gossip 过程是异步的，也就是说发消息的节点不会关注对方是否收到，即不等待响应；不管对方有没有收到，它都会每隔 1 秒向周围节点发消息。异步是它的优点，而消息冗余则是它的缺点。

 

这里一共有 16 个节点，节点 1 为初始被感染节点，通过 Gossip 过程，最终所有节点都被感染：

 

1.50

 

 

Gossip 的特点（优势）

1）扩展性

网络可以允许节点的任意增加和减少，新增加的节点的状态最终会与其他节点一致。

2）容错

网络中任何节点的宕机和重启都不会影响 Gossip 消息的传播，Gossip 协议具有天然的分布式系统容错特性。

3）去中心化

Gossip 协议不要求任何中心节点，所有节点都可以是对等的，任何一个节点无需知道整个网络状况，只要网络是连通的，任意一个节点就可以把消息散播到全网。

4）一致性收敛

Gossip 协议中的消息会以一传十、十传百一样的指数级速度在网络中快速传播，因此系统状态的不一致可以在很快的时间内收敛到一致。消息传播速度达到了 logN。

5）简单

Gossip 协议的过程极其简单，实现起来几乎没有太多复杂性。

Márk Jelasity 在它的 Gossip一书中对其进行了归纳：

 

Gossip 的缺陷

分布式网络中，没有一种完美的解决方案，Gossip 协议跟其他协议一样，也有一些不可避免的缺陷，主要是两个：

1）消息的延迟

由于 Gossip 协议中，节点只会随机向少数几个节点发送消息，消息最终是通过多个轮次的散播而到达全网的，因此使用 Gossip 协议会造成不可避免的消息延迟。不适合用在对实时性要求较高的场景下。

2）消息冗余

Gossip 协议规定，节点会定期随机选择周围节点发送消息，而收到消息的节点也会重复该步骤，因此就不可避免的存在消息重复发送给同一节点的情况，造成了消息的冗余，同时也增加了收到消息的节点的处理压力。而且，由于是定期发送，因此，即使收到了消息的节点还会反复收到重复消息，加重了消息的冗余。

 

 

Gossip 类型

Gossip 有两种类型：

• Anti-Entropy（反熵）：以固定的概率传播所有的数据
• Rumor-Mongering（谣言传播）：仅传播新到达的数据

Anti-Entropy 是 SI model，节点只有两种状态，Suspective 和 Infective，叫做 simple epidemics。

Rumor-Mongering 是 SIR model，节点有三种状态，Suspective，Infective 和 Removed，叫做 complex epidemics。

其实，Anti-entropy 反熵是一个很奇怪的名词，之所以定义成这样，Jelasity 进行了解释，因为 entropy 是指混乱程度（disorder），而在这种模式下可以消除不同节点中数据的 disorder，因此 Anti-entropy 就是 anti-disorder。换句话说，它可以提高系统中节点之间的 similarity。

在 SI model 下，一个节点会把所有的数据都跟其他节点共享，以便消除节点之间数据的任何不一致，它可以保证最终、完全的一致。

由于在 SI model 下消息会不断反复的交换，因此消息数量是非常庞大的，无限制的（unbounded），这对一个系统来说是一个巨大的开销。

 

但是在 Rumor Mongering（SIR Model） 模型下，消息可以发送得更频繁，因为消息只包含最新 update，体积更小。而且，一个 Rumor 消息在某个时间点之后会被标记为 removed，并且不再被传播，因此，SIR model 下，系统有一定的概率会不一致。

而由于，SIR Model 下某个时间点之后消息不再传播，因此消息是有限的，系统开销小。

 

Gossip 中的通信模式

在 Gossip 协议下，网络中两个节点之间有三种通信方式:

• Push: 节点 A 将数据 (key,value,version) 及对应的版本号推送给 B 节点，B 节点更新 A 中比自己新的数据
• Pull：A 仅将数据 key, version 推送给 B，B 将本地比 A 新的数据（Key, value, version）推送给 A，A 更新本地
• Push/Pull：与 Pull 类似，只是多了一步，A 再将本地比 B 新的数据推送给 B，B 则更新本地

如果把两个节点数据同步一次定义为一个周期，则在一个周期内，Push 需通信 1 次，Pull 需 2 次，Push/Pull 则需 3 次。虽然消息数增加了，但从效果上来讲，Push/Pull 最好，理论上一个周期内可以使两个节点完全一致。直观上，Push/Pull 的收敛速度也是最快的。

 

 

复杂度分析

对于一个节点数为 N 的网络来说，假设每个 Gossip 周期，新感染的节点都能再感染至少一个新节点，那么 Gossip 协议退化成一个二叉树查找，经过 LogN 个周期之后，感染全网，时间开销是 O(LogN)。由于每个周期，每个节点都会至少发出一次消息，因此，消息复杂度（消息数量 = N * N）是 O(N^2) 。注意，这是 Gossip 理论上最优的收敛速度，但是在实际情况中，最优的收敛速度是很难达到的。

 

假设某个节点在第 i 个周期被感染的概率为 pi，第 i+1 个周期被感染的概率为 pi+1 ，

1）则 Pull 的方式:

 

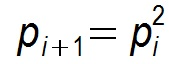
2）Push 方式：

 

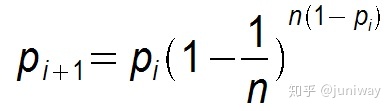
显然 Pull 的收敛速度大于 Push ，而每个节点在每个周期被感染的概率都是固定的 p (0<p<1)，因此 Gossip 算法是基于 p 的平方收敛，也称为概率收敛，这在众多的一致性算法中是非常独特的。

 https://www.backendcloud.cn/2017/11/12/raft-gossip/

Raft算法和Gossip协议

简单介绍下集群数据同步，集群监控用到的两种常见算法。

Raft算法

raft 集群中的每个节点都可以根据集群运行的情况在三种状态间切换：follower, candidate 与 leader。leader 向 follower 同步日志，follower 只从 leader 处获取日志。在节点初始启动时，节点的 raft 状态机将处于 follower 状态并被设定一个 election timeout，如果在这一时间周期内没有收到来自 leader 的 heartbeat，节点将发起选举：节点在将自己的状态切换为 candidate 之后，向集群中其它 follower 节点发送请求，询问其是否选举自己成为 leader。当收到来自集群中过半数节点的接受投票后，节点即成为 leader，开始接收保存 client 的数据并向其它的 follower 节点同步日志。leader 节点依靠定时向 follower 发送 heartbeat 来保持其地位。任何时候如果其它 follower 在 election timeout 期间都没有收到来自 leader 的 heartbeat，同样会将自己的状态切换为 candidate 并发起选举。每成功选举一次，新 leader 的步进数都会比之前 leader 的步进数大1。

Raft一致性算法处理日志复制以保证强一致性。

follower 节点不可用

follower 节点不可用的情况相对容易解决。因为集群中的日志内容始终是从 leader 节点同步的，只要这一节点再次加入集群时重新从 leader 节点处复制日志即可。

leader 不可用

一般情况下，leader 节点定时发送 heartbeat 到 follower 节点。

 

 

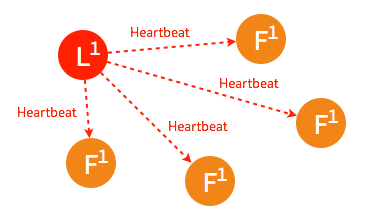
由于某些异常导致 leader 不再发送 heartbeat ，或 follower 无法收到 heartbeat 。

 

 

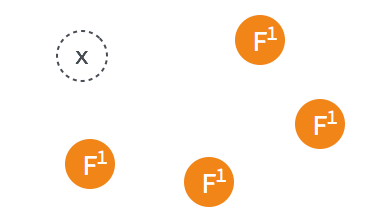
当某一 follower 发生 election timeout 时，其状态变更为 candidate，并向其他 follower 发起投票。

 

 

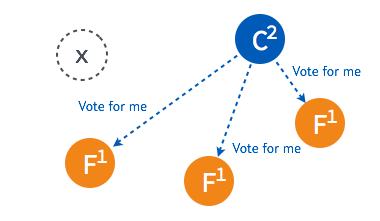
当超过半数的 follower 接受投票后，这一节点将成为新的 leader，leader 的步进数加1并开始向 follower 同步日志。

 

 

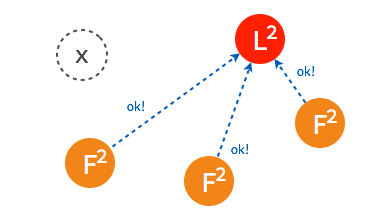
当一段时间之后，如果之前的 leader 再次加入集群，则两个 leader 比较彼此的步进数，步进数低的 leader 将切换自己的状态为 follower。

 

 

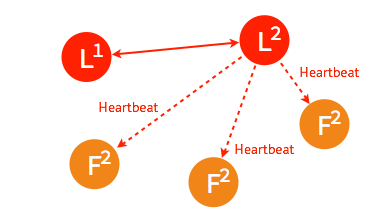
较早前 leader 中不一致的日志将被清除，并与现有 leader 中的日志保持一致。

 

 

Gossip协议

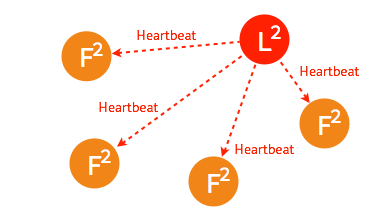
传统的监控，如ceilometer，由于每个节点都会向server报告状态，随着节点数量的增加server的压力随之增大。分布式健康检查可以解决这类性能瓶颈，降节点数量从数百台扩至数千台，甚至更多。

Agent在每台节点上运行，可以在每个Agent上添加一些健康检查的动作，Agent会周期性的运行这些动作。用户可以添加脚本或者请求一个URL链接。一旦有健康检查报告失败，Agent就把这个事件上报给服务器节点。用户可以在服务器节点上订阅健康检查事件，并处理这些报错消息。

在所有的Agent之间（包括服务器模式和普通模式）运行着Gossip协议。服务器节点和普通Agent都会加入这个Gossip集群，收发Gossip消息。每隔一段时间，每个节点都会随机选择几个节点发送Gossip消息，其他节点会再次随机选择其他几个节点接力发送消息。这样一段时间过后，整个集群都能收到这条消息。示意图如下。

 

 

Gossip协议已经是P2P网络中比较成熟的协议了。Gossip协议的最大的好处是，即使集群节点的数量增加，每个节点的负载也不会增加很多，几乎是恒定的。这就允许Consul管理的集群规模能横向扩展到数千个节点。

Consul的每个Agent会利用Gossip协议互相检查在线状态，本质上是节点之间互Ping，分担了服务器节点的心跳压力。如果有节点掉线，不用服务器节点检查，其他普通节点会发现，然后用Gossip广播给整个集群。

Gossip算法又被称为反熵（Anti-Entropy），熵是物理学上的一个概念，代表杂乱无章，而反熵就是在杂乱无章中寻求一致，这充分说明了Gossip的特点：在一个有界网络中，每个节点都随机地与其他节点通信，经过一番杂乱无章的通信，最终所有节点的状态都会达成一致。每个节点可能知道所有其他节点，也可能仅知道几个邻居节点，只要这些节可以通过网络连通，最终他们的状态都是一致的，当然这也是疫情传播的特点。

要注意到的一点是，即使有的节点因宕机而重启，有新节点加入，但经过一段时间后，这些节点的状态也会与其他节点达成一致，也就是说，Gossip天然具有分布式容错的优点。