经典算法面试题：LeetCode两个有序数组中位数

Leetcode算法系列将详细讲解一些经典的面试算法题。

今天的算法是LeetCode中第四个题目，Median of Two Sorted Arrays，也就是给定两个有序数组求出中位数。

 

理解题意

首先给定的是两个有序数组，比如{1,3}以及{2}，那么合并这两个数组就是{1,2,3}，因此很显然中位数是2；

再给定两个数组{1,3}和{2,4}，那么合并这两个数组就是{1,2,3,4}，因此中位数就是(2+3)/2，也就是2.5；

理解了题意后该如何解决这个问题呢？

 

思路1：最直观解法

对于各种各样的算法题来说通常都会有一个最简单最直接的方法，在面试中如果你一下想不到最优解，那么首先提出一个最简单最直接的方案是比较好的方法，不要一下就去想最优解法，卡住后也不和面试官沟通，这会让面试官觉得你可能连最简单的解法都想不出来。

那么对于这个问题来说，最简单最直接的解法当然就是重新建立一个数组，然后按序合并这两个数组，这样我们就得到了一个完整的数组，比如对于{1,3}和{2}来说，我们对其进行合并这样就得到了{1,2,3}，因为合并后的数组是有序的，因此我们可以直接计算出中位数。

上面的这种解法是相当直观的，让我们来分析一下这个题目的时间和空间复杂度，所谓“时间复杂度”是说对于给定数据规模你的算法需要多少次操作，比如数据规模是N个，你的算法对每个数据进行10次操作，那么你的时间复杂度就是10N，用算法的术语就是O(10N)；而所谓“空间复杂度”是说对于给定的数据规模你的算法需要多少内存，比如数据规模是N个，你的算法对于每个数据的处理都要新开辟6个内存单元(这里的单元是依据具体情况的，可以是一个int，一个bool或者一个复杂的对象等)，那么你的空间复杂度就是6N，即O(6N)。

有了时间和空间复杂度的概念，让我们来分析一下。

首先我们要开辟一个新的数组，该数组的长度是原来两个数组的和，假设这两个数组的长度是M和N，那么新的数组长度就是M+N，因此空间复杂度是O(M+N)。

创建出新的数组后我们要合并原来的两个数组，合并过程相对简单，只需要依次遍历一遍这两个数组即可，仅此时间复杂度也是O(M+N)。

显然最简单的解法过不了面试，那么该如何改进呢？

 

思路2：二分查找

注意这里给的是两个有序数组，对于有序数组的搜索来说最常用的就是二分搜索，二分搜索中每次都可以丢一半的数据，大大加快了搜索速度。

那么具体到这里该如何应用二分查找的思想呢？

首先找到数组中位数是一个很具体的问题，在《一道决定面试成败的算法题》这篇文章中我们说过，有时一个具体的问题反而不如一个通用的问题容易求解，在这里这个通用的问题就是“找到数组中第K大的数”，如果这个问题得到了解决，那么原题就不在话下。

但是这里题目给的是两个数组，我们该如何利用二分查找的思想每次都丢掉一部分数据呢？

二分搜索中每次都找到数组最中间的一个数字开始比较，而这里有两个数组，要想找到这里的“中间数字”就会有两个，每个数组各自一个。因此我们需要对这两个数组进行划分，假设有两个数组：数组A和数组B，我们需要从数组A和数组B中各自划分出一段，并且这两段的长度就是K，如图所示：

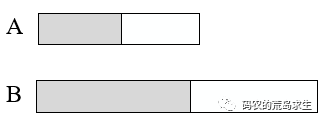
我们将数组A的左部称为AL，右部称为AR，相应的B的左部称为BL，右部称为BR，其中AL+BL的数字个数是K。

这样我们就得到了两个数组的“中间数字”，并且这两个中间数字只可能有三种情况：相等，大于或小于。

如果这两个中间数字相等，那么就很简单了，这两个数组的第K个数就是这两个中间数字，这是显而易见的，难点在于不等的情况。

假如数组A的中间数字是10，数组B的中间数字是2：

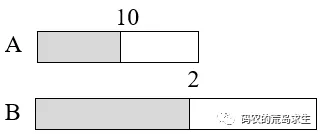
那么我们可以得出以下两个结论：

• 这两个数组的第K大的数一定不在数组A中间数字10的右部

• 这两个数组的第K大的数一定不在数组B中间数字2的左部

我们来简单的证明一下。

假设第K大的数字出现在了数组A中间数字10的右部，那么k一定大于10，因此将AL和BL合并后K也一定出现在10的右边，但是不要忘了AL+BL的个数是k个，现在第K大的数字跑到了10的右边，这显然是矛盾的，因此第K大的数一定不在数组A中间数字10的右部，如图所示：

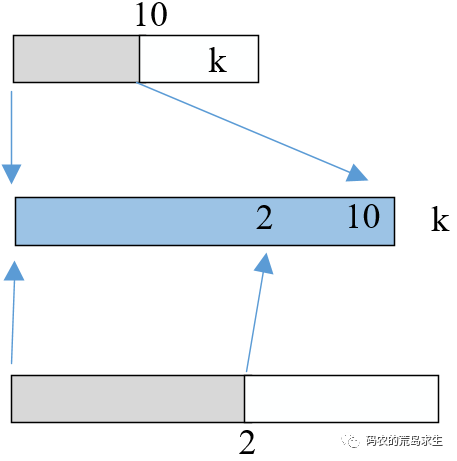
假如第K大的数字出现在了数组B中间数字2的左部，因此k一定小于2，那么将AL和BL合并后K也一定出现在2的左边，同时AL也会有一部分合并到2的左边，最极端情况就是只有10位于2的右边，其它所有数字都在2的左边，这就出现矛盾点了，因为AL+BL的个数是K个，但是现在这个数字居然出现在了2的左边，因此k一定不在数组B的左部，如图所示：

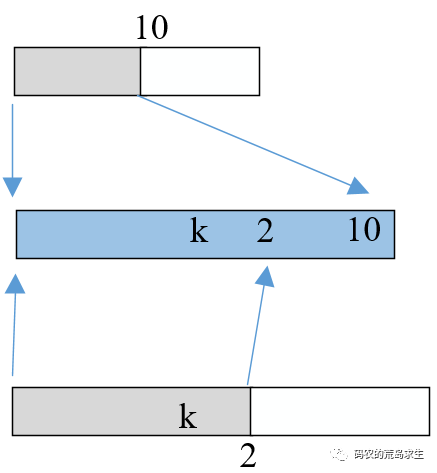
有了这样的结论每次比较两个中间数字后都可以丢掉两个数组的一部分，因此可以快速减小问题规模。

当数组A的中间数字小于数组B的中间数字时有同样的结论，有了这样的分析代码就很简单了。

 

代码实现

int findKInSortedArrays(vector<int>& A, int b, int e,                      vector<int>& B, int f, int s,                      int k) {  if (b > e)    return B[f+k-1];  if (f > s)    return A[b+k-1];  if (k == 1)    return min(A[b], B[f]);  if (e-b > s-f)    return findKInSortedArrays(B,f,s,A,b,e,k);
  int lenA = min(k/2, e-b+1);  int lenB = k - lenA;  if (A[b+lenA-1] == B[f+lenB-1])    return A[b+lenA-1];  else if (A[b+lenA-1] < B[f+lenB-1])    return findKInSortedArrays(A, b+lenA,e,B,f,f+lenB-1,k-lenA);  else    return findKInSortedArrays(A,b,b+lenA-1,B,f+lenB,s,k-lenB);}double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {    int sizeA = nums1.size();    int sizeB = nums2.size();
    if ((sizeA+sizeB) % 2 == 1)        return findKInSortedArrays(nums1,0,sizeA-1, nums2,0,sizeB-1,(sizeA+sizeB)/2 + 1);    else        return (findKInSortedArrays(nums1,0,sizeA-1, nums2,0,sizeB-1,(sizeA+sizeB)/2) +                findKInSortedArrays(nums1,0,sizeA-1, nums2,0,sizeB-1,(sizeA+sizeB)/2 + 1)) / 2.0;}

代码相当直观，这里就不再多解释了。

该实现没有申请额外的内存空间因此空间复杂度为O(1)，时间复杂度O(log(M+N))，该算法速度相当快，超过了LeetCode中90%的C++算法实现，如果将递归改为循环速度预期会进一步加快。

 

结论

实际上这个题目的思考范围依然没有跳出“二分查找”的思想，找出两个参照数字，比较后丢掉问题的一部分，这里再一次印证了算法是各种各样千奇百怪的，但是这背后的思想就那么多，我们看到一个算法不要仅仅去“记住”问题的解，而是要了解这个算法是怎么来的，只有做到这一点才能真正以不变应万变。

 

//        assert args.length >5; // -ea