98.验证二叉搜索树 Golang实现「自顶向下」

题目描述：

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左
子树
只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

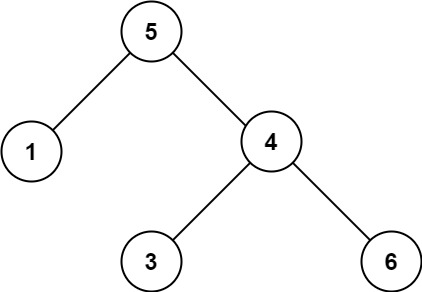
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

思路分析：

递归问题有两种解题思路：

使用 自顶向下：

• 决策依赖父节点的状态：当当前节点的决策依赖于父节点（或祖先节点）的状态时，通常使用自顶向下递归。例如，判断树是否为二叉搜索树（BST），每个节点都需要知道其父节点的有效范围。
• 有条件提前终止：如果可以在递归的过程中提早终止（例如发现某个条件不满足就停止），那么通常使用自顶向下的递归方式。
• 状态传递较为简单：如果需要将状态信息（如最小值、最大值等）从上到下传递给每个子树，可以使用自顶向下递归。
  使用 自底向上：
• 子问题合并：当每个子问题的解是基于其子树或子问题的解来计算时，通常使用自底向上的递归。例如，计算树的深度、求解子树的最大路径和等。
• 动态规划问题：动态规划问题通常需要先解决最小的子问题，然后通过组合它们来得到最终解。这种方法是自底向上的。
• 问题拆解成多个子问题：当问题可以被拆解为多个较小的子问题，每个子问题独立解决并返回一个结果时，自底向上的方法通常更有效。

本题陷阱：二叉树是根节点的值大于所有右子树的值！

关键点（采用自顶向下）：

• 每个节点即时判断：当我们递归到一个节点时，首先判断它的值是否在允许的范围内（由其父节点和祖先节点决定）。如果不符合，立刻返回 false。否则继续递归其左右子树。
• 递归到底层节点时（叶子节点）：当递归到达叶子节点时，我们并不是直接返回 true，而是返回它是否满足当前节点的条件（即父节点和祖先节点所定义的有效值范围）。如果没有违反条件，才认为这个叶子节点是有效的，才会继续返回 true。

点击查看代码

func isValidBST(root *TreeNode) bool {
    return isValidBSTHelper(root, nil, nil)
}

func isValidBSTHelper(root *TreeNode,min,max *TreeNode)bool{
    if root==nil{
        return true
    }
    if (min != nil && root.Val <= min.Val) || (max != nil && root.Val >= max.Val) {
        return false
    }
    // 递归检查左子树和右子树
    return isValidBSTHelper(root.Left, min, root) && isValidBSTHelper(root.Right, root, max)
}