题目:
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
思路分析:
我们通过二分查找一个较短的数组的某个切分点,计算出另一个数组对应的切分点,从而找到中位数。
问题分解:
输入:两个已排序的数组 nums1 和 nums2。
目标:找出这两个数组合并后有序数组的中位数。
要求:时间复杂度为 O(log(m + n))。
关键思路:
-
[1 ] 中位数的定义:
假设一个数组长度为m,
对于奇数长度的合并数组,中位数是正中间的那个数,对应下标为m/2。
对于偶数长度的合并数组,中位数是中间两个数的平均值,对应下标为(m-1)/2,m/2。
下面为了统一不区分奇数偶数,可以使用:(m+1)/2,涉及到一个很关键的点,就是计算机的整除只取整数部分,即整体有几个偶数。如果原本是偶数,那么计算后的下标(m+1)/2,指向第二个数。而保证了第一个数:无论奇数偶数长度,都在这个下标的左侧。从而达到了统一公式的目的。那么合并两个数组,不确定哪个数组是奇数偶数,只需要记录下来分类点,从而可以获取到左右两侧的值。 -
[2 ] 不直接合并数组:
如果简单地合并数组再取中位数,时间复杂度是 O(m + n),不符合题目要求。
我们可以通过二分查找,将问题转换为寻找“两个数组的切分点”,使得切分线左边的数都小于右边的数。 -
[ 3] 二分查找的核心思想:
先选定较短的数组 nums1,假设长度为 m,较长的数组 nums2 长度为 n。
我们在较短的数组 nums1 上进行二分搜索,找到一个合适的切分点 i。
根据 i,可以计算出 nums2 的切分点 j = (m + n + 1) / 2 - i,这样保证总是有 (m + n + 1) / 2 个元素在左边。因为中位数在有序列表中的位置必然是合并后的数组的中间位置! -
[ 4] 找到中位数的条件:
目标是找到两个切分点 i 和 j,使得:
nums1[i-1] ≤ nums2[j]
nums2[j-1] ≤ nums1[i]
也就是说,左边的最大值小于等于右边的最小值。如果这两个条件成立,那么说明切分点是合理的,可以得到最终中位数。
调整切分点:
如果 nums1[i-1] > nums2[j],说明 i 太大了,需要左移。
如果 nums2[j-1] > nums1[i],说明 i 太小了,需要右移。
通过不断调整 i,最终可以找到一个满足条件的切分点。
中位数的计算:
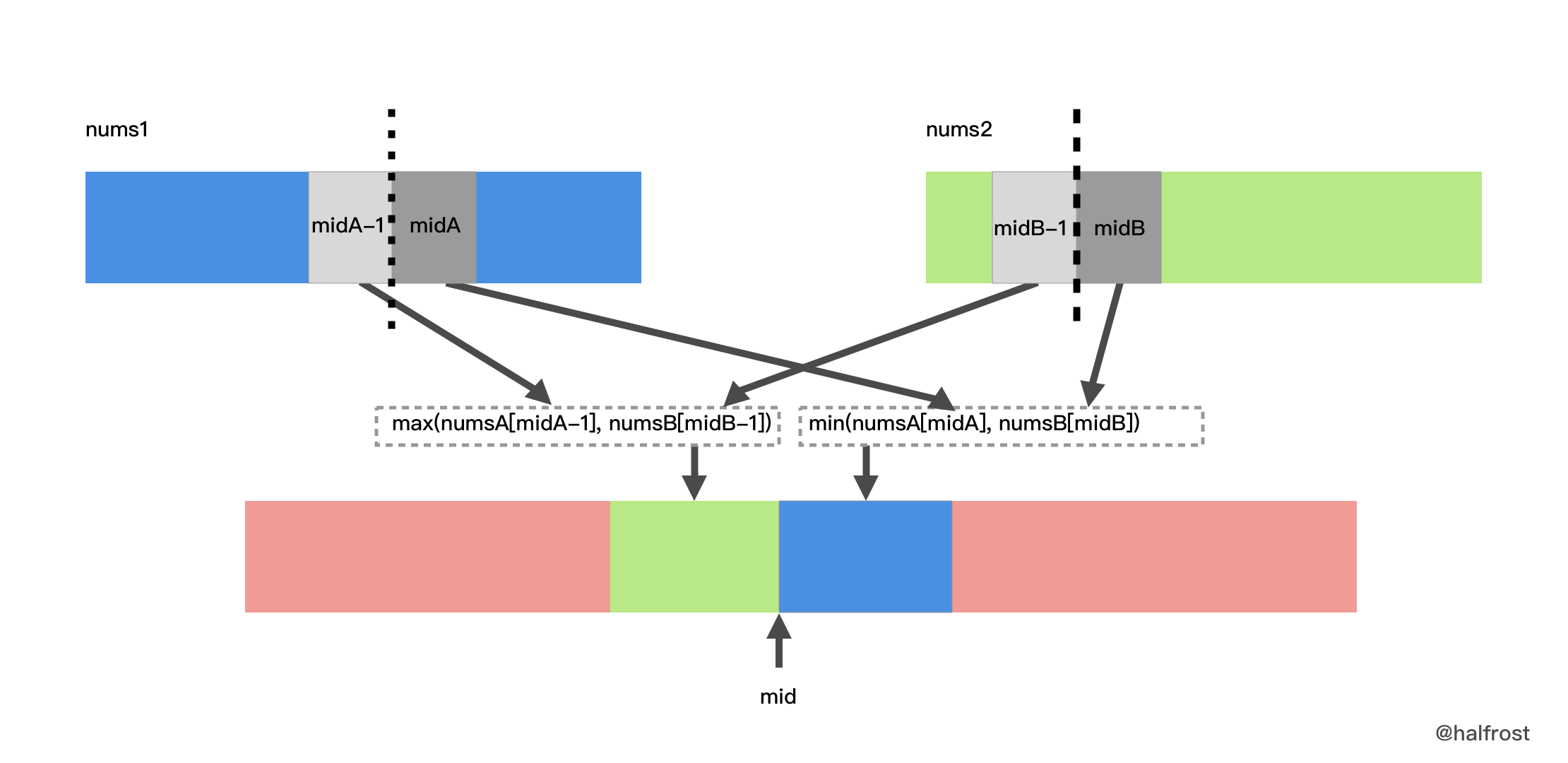
如果 m + n 是奇数,那么中位数就是左边部分的最大值,即 max(nums1[i-1], nums2[j-1])。
如果 m + n 是偶数,那么中位数是左边最大值和右边最小值的平均值,即 (max(nums1[i-1], nums2[j-1]) + min(nums1[i], nums2[j])) / 2。
具体步骤:
-
[ 1] 初始化:
让 nums1 的长度为 m,nums2 的长度为 n。
保证 nums1 的长度小于等于 nums2,即 m ≤ n。 -
[2 ] 二分查找:
在 nums1 上进行二分搜索。设定 i 为 nums1 的切分点,j 为 nums2 的切分点,满足 j = (m + n + 1) / 2 - i。通过二分调整 i 的位置,直到满足 nums1[i-1] ≤ nums2[j] 且 nums2[j-1] ≤ nums1[i]。
找到切分点:如果找到满足条件的切分点,计算中位数:
如果 m + n 是奇数,中位数就是左半部分的最大值。
如果 m + n 是偶数,中位数是左半部分的最大值与右半部分的最小值的平均值。 -
[3 ] 边界情况:
当 i 或 j 为 0 或 m 时,需要特别处理,因为此时可能没有左边或右边的元素。
边界处理情况详细说明:
-
nums1Mid == 0 和 nums1Mid == m 的情况:
-
nums2Mid == 0 和 nums2Mid == n 的情况:
点击查看代码
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
if len(nums1) > len(nums2) {
return findMedianSortedArrays(nums2, nums1)
}
m, n := len(nums1), len(nums2)
low, high, k := 0, m, (m+n+1)/2
var nums1Mid, nums2Mid int
for low <= high {
nums1Mid = low + (high - low) / 2
nums2Mid = k - nums1Mid
if nums1Mid > 0 && nums1[nums1Mid-1] > nums2[nums2Mid] {
// nums1Mid is too large, need to decrease
high = nums1Mid - 1
} else if nums1Mid < m && nums1[nums1Mid] < nums2[nums2Mid-1] {
// nums1Mid is too small, need to increase
low = nums1Mid + 1
} else {
// Found the correct partition
break
}
}
// Determine left half's maximum
var midLeft int
if nums1Mid == 0 {
midLeft = nums2[nums2Mid-1]
} else if nums2Mid == 0 {
midLeft = nums1[nums1Mid-1]
} else {
midLeft = max(nums1[nums1Mid-1], nums2[nums2Mid-1])
}
// If total length is odd, return the left side's maximum
if (m+n) % 2 == 1 {
return float64(midLeft)
}
// Determine right half's minimum
var midRight int
if nums1Mid == m {
midRight = nums2[nums2Mid]
} else if nums2Mid == n {
midRight = nums1[nums1Mid]
} else {
midRight = min(nums1[nums1Mid], nums2[nums2Mid])
}
// Return the average of the two middle values
return float64(midLeft + midRight) / 2.0
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号