初三奥赛模拟测试3
前言
我们的 \(Shadow\) 又 \(41\) 秒 \(AC\) \(T0\) 啦!

是的又换题了,大多数人都做过,但是我没做过啊 \(qwq\) 。
于是从别的地方扒了 \(4\) 道题,前两道是 \(NOIP\) 模拟赛的题,后两道从 \(NOI\) 模拟赛扒来的,知识点根本不会 \(qwq\) 。
T1 网络图
点击查看题面

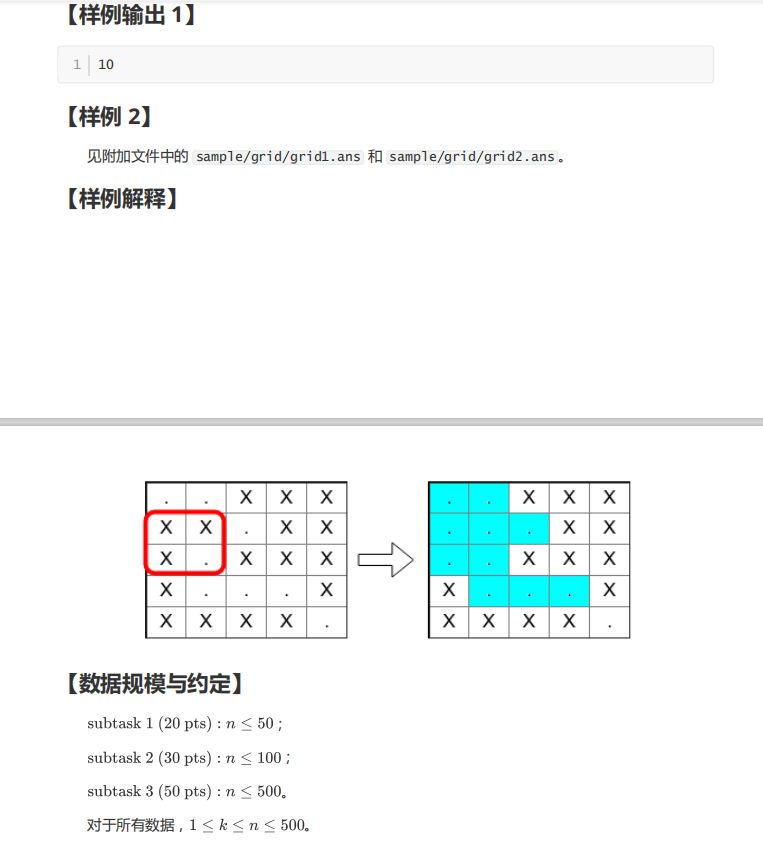
-
部分分 \(50pts\) :
暴力 \(O(n^4)\) 枚举 \(k\times k\) 矩形每次跑 \(dfs(bfs)\) 求连通块。
点击查看代码
#include<bits/stdc++.h> #define int long long #define endl '\n' using namespace std; const int N=1010; template<typename Tp> inline void read(Tp&x) { x=0;register bool z=true; register char c=getchar(); for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0; for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); x=(z?x:~x+1); } int n,m,cnt,t[N*N],ans; char s[N][N],ss[N][N]; bool v[N][N]; struct aa { int x,y; }; int h[4]={-1,1,0,0},z[4]={0,0,-1,1}; int bfs(int x,int y) { queue<aa>q; q.push({x,y}); v[x][y]=1; int ans=0; while(!q.empty()) { aa e=q.front(); int xx=e.x,yy=e.y; q.pop(); ans++; for(int k=0;k<4;k++) { int i=xx+h[k],j=yy+z[k]; if(!v[i][j]&&s[i][j]=='.'&&i>=1&&i<=n&&j>=1&&j<=n) v[i][j]=1, q.push({i,j}); } } return ans; } signed main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); freopen("out.txt","w",stdout); #endif read(n),read(m); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>s[i][j], ss[i][j]=s[i][j]; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { for(int i1=i;i1<=i+m-1;i1++) for(int j1=j;j1<=j+m-1;j1++) s[i1][j1]='.'; memset(v,0,sizeof(v)); if(!v[i][j]&&s[i][j]=='.') ans=max(ans,bfs(i,j)); for(int i1=i;i1<=i+m-1;i1++) for(int j1=j;j1<=j+m-1;j1++) s[i1][j1]=ss[i1][j1]; } cout<<ans; } -
正解:
先跑一遍 \(dfs(bfs)\) 预处理出每个连通块的编号与大小,以及每个点属于哪一个联通块。
然后去枚举 \(k\times k\) 矩形的位置,发现已经 \(O(n^2)\) 了,如果再每次处理其内部的情况肯定会 \(TLE\) 。
发现 \(k\times k\) 矩形每次就是往右移一位,那么减去矩形左边那一列的贡献,再加上新的这一列的贡献即可,类似于滑动窗口。
当然每一行的开头与结尾需要特殊处理,不过复杂度已经优化得可以接受了。
答案就是与 \(k\times k\) 矩阵相邻的一圈的贡献加上 \(k\times k\) ,当然矩阵 内部的会算重复,所以也是类似于滑动窗口的顺便处理其内部即可。
复杂度 \(O(n^2k)\) 。
点击查看代码
#include<bits/stdc++.h> #define int long long #define endl '\n' using namespace std; const int N=1010; template<typename Tp> inline void read(Tp&x) { x=0;register bool z=true; register char c=getchar(); for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0; for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); x=(z?x:~x+1); } int n,m,cnt,t[N*N],ans,to[N][N],sum; char s[N][N],ss[N][N]; bool v[N][N],vis[N*N]; struct aa { int x,y; }; int h[4]={-1,1,0,0},z[4]={0,0,-1,1}; int bfs(int x,int y) { queue<aa>q; q.push({x,y}); v[x][y]=1; to[x][y]=cnt; int ans=0; while(!q.empty()) { aa e=q.front(); int xx=e.x,yy=e.y; q.pop(); ans++; for(int k=0;k<4;k++) { int i=xx+h[k],j=yy+z[k]; if(!v[i][j]&&s[i][j]=='.'&&i>=1&&i<=n&&j>=1&&j<=n) v[i][j]=1, q.push({i,j}), to[i][j]=cnt; } } return ans; } signed main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); freopen("out.txt","w",stdout); #endif read(n),read(m); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>s[i][j], ss[i][j]=s[i][j]; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(!v[i][j]&&s[i][j]=='.') { cnt++; int tmp=bfs(i,j); t[cnt]=tmp; } for(int i=m;i<=n;i++) for(int j=m;j<=n;j++) { if(j==m) { for(int k=i-m+1;k<=i;k++) for(int l=j-m+1;l<=j;l++) if(s[k][l]=='.') t[to[k][l]]--; } else { for(int k=i-m+1;k<=i;k++) if(s[k][j-m]=='.') t[to[k][j-m]]++; for(int k=i-m+1;k<=i;k++) if(s[k][j]=='.') t[to[k][j]]--; } sum=0; if(i-m>=1) for(int k=j-m+1;k<=j;k++) sum+=(vis[to[i-m][k]]==0)*t[to[i-m][k]], vis[to[i-m][k]]=1; if(i+1<=n) for(int k=j-m+1;k<=j;k++) sum+=(vis[to[i+1][k]]==0)*t[to[i+1][k]], vis[to[i+1][k]]=1; if(j-m>=1) for(int k=i-m+1;k<=i;k++) sum+=(vis[to[k][j-m]]==0)*t[to[k][j-m]], vis[to[k][j-m]]=1; if(j+1<=n) for(int k=i-m+1;k<=i;k++) sum+=(vis[to[k][j+1]]==0)*t[to[k][j+1]], vis[to[k][j+1]]=1; if(i-m>=1) for(int k=j-m+1;k<=j;k++) vis[to[i-m][k]]=0; if(i+1<=n) for(int k=j-m+1;k<=j;k++) vis[to[i+1][k]]=0; if(j-m>=1) for(int k=i-m+1;k<=i;k++) vis[to[k][j-m]]=0; if(j+1<=n) for(int k=i-m+1;k<=i;k++) vis[to[k][j+1]]=0; if(j==n) for(int k=i-m+1;k<=i;k++) for(int l=j-m+1;l<=j;l++) if(s[k][l]=='.') t[to[k][l]]++; ans=max(ans,sum+m*m); } cout<<ans; }
T2 序列问题
点击查看题面


-
部分分:
-
\(20pts\) :
暴力 \(dfs\) \(O(2^n)\) 枚举每个点删或不删。
-
\(45pts\) :
考虑 \(DP\) 。
用 \(f_i\) 表示处理 \(1\sim i\) 这些数,并且该序列以 \(a_i\) 结尾的最优答案。
首先 \(f_i\) 合法,需要 \(a_i\leq i\) 。
一个 \(j\) 转移到 \(i\) 需要满足:
- \(j<i\)
- \(a_j<a_i\)
- \(a_i-a_j\leq i-j\)
于是有:
\[f_{i}=max(f_j+((j<i\&\&a_j<a_i\&\&a_i-a_j<i-j)?1:0)) \]复杂度 \(O(n^2)\) 。
点击查看代码
#include<bits/stdc++.h> using namespace std; long long n,dis[500100],dp[500100],a[500100],in,siz,ans; int main() { freopen("sequence.in","r",stdin); freopen("sequence.out","w",stdout); scanf("%lld",&n); for(int i=1;i<=n;i++) { scanf("%lld",&a[i]); dis[i]=i-a[i]; } for(int i=1;i<=n;i++) { for(int j=0;j<i;j++) { if(dis[j]<=dis[i]&&dis[i]-dis[j]<=i-j-1&&dis[j]>=0&&dis[i]>=0) dp[i]=max(dp[j]+1,dp[i]); } ans=max(ans,dp[i]); } printf("%lld\n",ans); return 0; }
-
-
正解:
对于这三个限制:
- \(j<i\)
- \(a_j<a_i\)
- \(a_i-a_j\leq i-j\)
发现只要满足后两个则第一个一定满足。
那么将 \(a_i\) 从小到大排序,然后求一个对于 \(i-a_i\) 的最长不下降子序列(\(i\) 指排序前的 \(i\))。
但是发现对于 \(a_i=a_j\) 的情况会造成影响。
那么可以在排序的时候使 \(a_i=a_j\) 的下标大的放前面,设 \(i>j\) ,则 \(i-a_i>j-a_j\) ,将 \(i-a_i\) 放前面就不会对求最长不下降子序列产生影响。
关于我之前只会 \(O(n^2)\) \(DP\) 求最长不下降子序列这件事。复杂度 \(O(n\log(n))\) 。
点击查看代码
#include<bits/stdc++.h> #define int long long #define endl '\n' using namespace std; const int N=5e5+10; template<typename Tp> inline void read(Tp&x) { x=0;register bool z=true; register char c=getchar(); for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0; for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); x=(z?x:~x+1); } int n,tot,c[N],b[N]; struct aa { int dr,id; }a[N]; bool cmp(aa a,aa b) {return a.dr==b.dr?a.id>b.id:a.dr<b.dr;} queue<int>q; signed main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); freopen("out.txt","w",stdout); #endif freopen("sequence.in","r",stdin); freopen("sequence.out","w",stdout); read(n); for(int i=1;i<=n;i++) read(a[i].dr), a[i].id=i; stable_sort(a+1,a+1+n,cmp); for(int i=1;i<=n;i++) if(a[i].id-a[i].dr>=0) q.push(a[i].id-a[i].dr); while(!q.empty()) b[++tot]=q.front(), q.pop(); c[1]=b[1]; int len=1; for(int i=2;i<=tot;i++) { if(b[i]>=c[len]) c[++len]=b[i]; else { int j=upper_bound(c+1,c+len+1,b[i])-c; c[j]=b[i]; } } cout<<len; }至于一些同学用树状数组优化 \(DP\) 从而达到 \(AC\) 的方法就不讨论了。
T3 置换
看不懂啥叫置换,超纲了,咕了咕了。
T4 同桌的你
基环树(虽然也可以不用),其实也可以学一学打的,懒得打了,挺麻烦的。
但是附上 \(wkh\) 的题解:

