题解:Fibonacci 前 n 项和 (矩阵乘法与快速幂)
前言
\(loj\) 上的题,题目链接 。
我们高级的 \(loj\) 又双叒叕卡死了,所以我用 \(vjudge\) 把 \(loj\) 绑上了。
题面
\(f_x=\begin{cases} 1&x\in\{1,2\}\\ f_{x-1}+f_{x-2}&x \geq 3\\ \end{cases}\)
定义 \(s_x=\sum\limits_{i=1}^nf_i\) 。
求 \(s_n\) 。
方法一
- 结论:
-
证明:
\(∵f_{n+2}=f_{n+1}+f_n\)
\(∴f_n=f_{n+2}-f_{n+1}\)
已知 \(s_n=f_n+f_{n-1}+…+f_1\)
\(∴s_n=f_{n+2}-f_{n+1}+f_{n-1}+…+f_1\)
又 \(∵ f_{n+1}=f_{n}+f_{n-1}\)
\(∴s_n=f_{n+2}-f_n+f_{n-2}+…+f_1\)
同理消去 \(f_{n}\) 和 \(f_{n-2}\)
得 \(s_n=f_{n+2}-f_{n+1}+f_{n-3}+…+f_3\)
如此循环,直到:
\(s_n=f_{n+2}-f_3+f_1\)
\(s_n=f_{n+2}-2+1\)
\(s_n=f_{n+2}-1\)
由此,通过矩阵乘法与快速幂求出 \(f_{n+2}\) ,再 \(-1\) 即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=10;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int n,P,ans[N][N],c[N][N],a[N][N];
void qpow(int b)
{
for(;b;b>>=1)
{
if(b&1)
{
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
for(int k=1;k<=2;k++)
(c[i][j]+=(ans[k][j]*a[i][k])%P)%P;
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
ans[i][j]=c[i][j],c[i][j]=0;
}
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
for(int k=1;k<=2;k++)
(c[i][j]+=(a[i][k]*a[k][j])%P)%P;
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
a[i][j]=c[i][j],c[i][j]=0;
}
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(n),read(P);
a[1][1]=1;
a[2][1]=1;
a[1][2]=1;
a[2][2]=0;
for(int i=1;i<=2;i++)
ans[i][i]=1;
qpow(n);
cout<<(ans[1][1]+ans[1][2]-1)%P;
}
方法二
-
前言:
其实第一次是用这个方法做的,当时发现一个小结论,但不知道怎么证明的,直接用就 \(A\) 了。
-
结论:
\(s_n=s_{n-1}+s_{n-2}+1\) 。
-
证明:
需要在已知 \(s_n=f_{n+2}-1\) 条件下证明。
\(∵ s_n=f_{n+2}-1\)
\(~~~~s_{n-1}=f_{n+1}-1\)
\(~~~~s_{n-2}=f_{n}-1\)
\(~~~~f_{n+2}=f_{n+1}+f_n\)
\(∴ s_n=f_{n+2}-1=f_{n+1}+f_{n}-1=s_{n-1}+s_{n-2}+1\)
于是就可以用和求 \(f_n\) 差不多大方式用矩阵乘法与快速幂求了。
将矩阵范围扩展到 \(3\times 3\),多出来那一维用来搞这个 \(+1\) 。
-
另一种证明方法:
好的的刚才 \(jjidawang\) 来教了不用 \(s_n=f_{n+2}-1\) 的方法。(2024年03月13日15:35:43)
\(∵ s_{n-1}=f_1+f_2+…+f_{n-2}+f_{n-1}\)
\(~~~~s_{n-2}=f_1+f_2+…+f_{n-2}\)
将其错开一位相加。
\(f_1+f_2+f_3+…+f_{n-1}\)
\(~~~~~~~~~+~~~~+~~~~~~~~~~~~~~~+\)
\(~~~~~~~~~f_1~~~~~f_2~~~~~~~~~~~~~~f_{n-2}\)
\(∵ f_x=f_{x-1}+f_{x-2}\)
从而得到 \(s_{n-1}+s_{n-2}=f_1+f_3+f_4+…+f_n\)
\(∴ s_n=f_1+f_2+f_3+…+f_n\)
\(~~~~~~~~=s_{n-1}+s_{n-2}+f_2\)
\(~~~~~~~~=s_{n-1}+s_{n-2}+1\)
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=10;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int n,P,ans[N][N],c[N][N],a[N][N];
void qpow(int b)
{
for(;b;b>>=1)
{
if(b&1)
{
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
for(int k=1;k<=3;k++)
(c[i][j]+=(ans[k][j]*a[i][k])%P)%P;
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
ans[i][j]=c[i][j],c[i][j]=0;
}
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
for(int k=1;k<=3;k++)
(c[i][j]+=(a[i][k]*a[k][j])%P)%P;
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
a[i][j]=c[i][j],c[i][j]=0;
}
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(n),read(P);
a[1][1]=1,a[1][2]=1,a[1][3]=1;
a[2][1]=1,a[2][2]=0,a[2][3]=0;
a[3][1]=0,a[3][2]=0,a[3][3]=1;
ans[1][1]=1,ans[2][2]=1,ans[3][3]=1;
qpow(n-2);
cout<<(2*ans[1][1]+ans[1][2]+ans[1][3])%P;
}
方法三
-
前言:
可能这才是官方正解吧。
因为前面的都是用结论堆的。
-
解法:
直接看图:
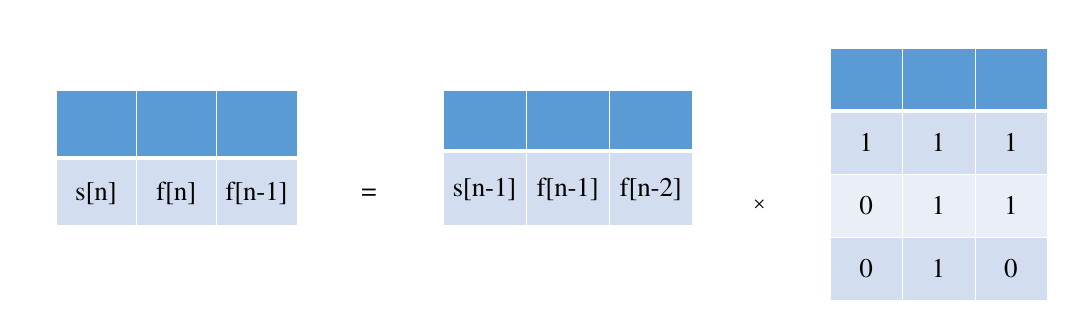
很好理解对吧。
所以和之前一样的:
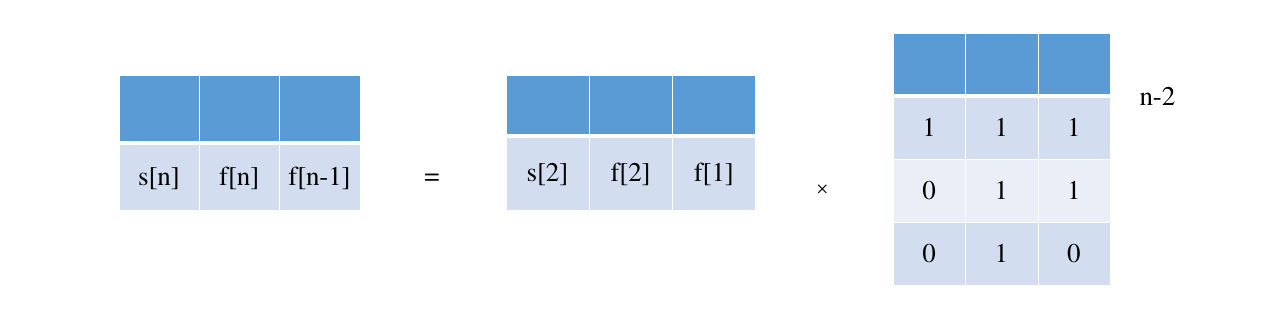
这里注意一下 \(s_2=2\) 即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=10;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int n,P,ans[N][N],c[N][N],a[N][N];
void qpow(int b)
{
for(;b;b>>=1)
{
if(b&1)
{
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
for(int k=1;k<=3;k++)
(c[i][j]+=(ans[k][j]*a[i][k])%P)%P;
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
ans[i][j]=c[i][j],c[i][j]=0;
}
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
for(int k=1;k<=3;k++)
(c[i][j]+=(a[i][k]*a[k][j])%P)%P;
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
a[i][j]=c[i][j],c[i][j]=0;
}
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(n),read(P);
a[1][1]=1,a[1][2]=1,a[1][3]=1;
a[2][1]=0,a[2][2]=1,a[2][3]=1;
a[3][1]=0,a[3][2]=1,a[3][3]=0;
for(int i=1;i<=3;i++)
ans[i][i]=1;
qpow(n-2);
cout<<(2*ans[1][1]+ans[1][2]+ans[1][3])%P;
}

