初三奥赛模拟测试1
前言
-
总分:\(107pts\)

-
\(T1~79pts:\)
坐标 \(DP\) ,赛时感觉打的是正解,但是打假了。
-
\(T2~28pts:\)
理解错题了,以为是帮他调程序了,于是给人家调 \(TLE\) 了。
-
\(T3~0pts,T4~0pts:\)
没啥好说的,不会。
T1 回文
点击查看题面

-
部分分:
部分分没什么好说的,大多集中在 \(79pts\) ,都是 \(DP\) 打假了的。
-
正解:
坐标 \(DP\) 。
\(4\) 维的很好想,对于回文串的性质,从前往后跑和从后往前跑路径是一样的。
那么定义 \(f[i][j][k][l]\) ,表示从前往后跑到 \(a[i][j]\) ,从后往前跑到 \(a[k][l]\) 时的方案数。
但是 \(4\) 维肯定会 \(MLE\) ,之后发现第 \(4\) 维可以去掉,因为从前往后和从后往前跑路径始终是保持相同的,所跑的步数也一定是相同的,那么第 \(4\) 维 \(l\) 完全可以用 \(i,j,k\) 表示。
-
解释一下:
从 \(a[1][1]\) 跑到 \(a[n][m]\) ,需要走的步数为 \(n+m-1\) ,起点不算,那么均分下来,两边各需跑 \(maxx=\dfrac{n+m-1}{2}\) 步。
那么对于从前往后的步数显然为 \(i+j-1\) ,起点不算,那么从后往前搜走的步数也一定是 \(i+j-1\) ;对于从后往前的步数同样的可以表示为 \((n-k+1)+(m-l+1)-1=i+j-1\) ,那么 \(l=m+n-i-j-k+2\) 。
所以定义 \(f[i][j][k]\) 即可,第 \(4\) 维不是消失了,是可以用前 \(3\) 维表示,不需要存了。
转移方程很好想,如果 \(a[i][j]=a[k][l]\) ,那么对于其下一步 \(f[i1][j1][k1]+=f[i][j][k]\) 即可。当然对于此时如果 \(i+j-1=maxx\) ,也就是已经匹配完了,就不需要转移了。
不好搞的是统计答案。
发现 \(m+n\) 奇偶不同时,统计答案也是不同的,若 \(n+m\) 为奇数时,他两边同时跑最后时到达一个点的;反之为偶数时,他最后会跑到相邻的两个点。
如图:
-
\(m+n\) 为奇数
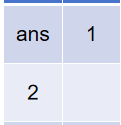
讨论到达 \(ans\) 的前一刻 \(k,l\) 可能的位置,如图 \(1,2\) ,所以对于 \(k\) 的位置可能为 \(i,i+1\) ,\(l\) 的位置不用讨论,\(k\) 确定同时也就确定了。
-
\(m+n\) 为偶数
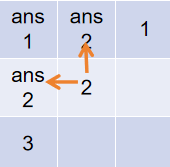
讨论 \(k,l\) 在到达 \(ans2\) 上一步时可能的位置,如图 \(1,2,3\) ,同时注意 \(2\) 的贡献有两次,所以要家两次。所以 \(k\) 的位置可能为 \(i,i+1,i+2\) ,其中 \(i+1\) 的情况要算两遍。
而至于 \(\%\) 的常数很大,可以打一个 \(mod\) 函数,看代码就知道了。
点击查看代码
#include<bits/stdc++.h> // #define int long long #define endl '\n' using namespace std; const int N=510,P=993244853; template<typename Tp> inline void read(Tp&x) { x=0;register bool z=true; register char c=getchar(); for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0; for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); x=(z?x:~x+1); } int n,m,maxx; unsigned int f[N][N][N],ans; char a[N][N]; int hx[5]={0,1,1,0,0},zx[5]={0,0,0,1,1},hy[5]={0,-1,0,-1,0},zy[5]={0,0,-1,0,-1}; void mod(unsigned int &x) {x=(x>=P?x-P:x);} signed main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); freopen("out.txt","w",stdout); #endif read(n),read(m); maxx=(n+m-1)/2; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin>>a[i][j]; if(a[1][1]!=a[n][m]) { cout<<0; return 0; } f[1][1][n]=1; for(int i=1;i<=n;i++) for(int j=1;i+j<=maxx+1&&j<=m;j++) for(int k=n;k>=i;k--) { int l=m+n-i-j+2-k; if(a[i][j]==a[k][l]) { if(i+j!=maxx+1) for(int x=1;x<=4;x++) { int i1=i+hx[x],j1=j+zx[x],k1=k+hy[x],l1=l+zy[x]; if(a[i1][j1]==a[k1][l1]) f[i1][j1][k1]+=f[i][j][k],mod(f[i1][j1][k1]); } } } if(!((m+n)&1)) for(int i=1;i<=min(n,maxx);i++) { for(int k=0;k<=2;k++) { int j=maxx-i+1; ans+=f[i][j][i+k],mod(ans); } ans+=f[i][maxx-i+1][i+1],mod(ans); } else for(int i=1;i<=min(n,maxx);i++) for(int k=0;k<=1;k++) { int j=maxx-i+1; ans+=f[i][j][i+k],mod(ans); } cout<<ans; }复杂度 \(O(n\times m\times n)\) 。
-
T2 快速排序
点击查看题面

-
部分分:
直接在给的快排函数上调,他那个代码时没有随机化的,会 \(TLE\) 的,所以我 \(TLE~28pts\) ,别人多少不知道了。
-
正解:
首先他那个快排是死的,我们自带的 \(stable\_sort\) 是有随机化的,直接用这个即可。
然后分析他这个代码(分析样例)。
对于当前位置如果是 \(nan\) 的话,就不动,直接输出。
否则,就将所有比他小的数,包括他自己输出即可,当然输出过的就不再输出了。
思路听起来很简单的,调代码就行了。
实现就比较简单了,每个人方法可能不一样,直接看代码吧。
点击查看代码
#include<bits/stdc++.h> #define int long long #define endl '\n' using namespace std; const int N=5e5+10; template<typename Tp> inline void read(Tp&x) { x=0;register bool z=true; register char c=getchar(); for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0; for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); x=(z?x:~x+1); } int t,n,b[N],tot,id[N]; string a[N]; bool v[N]; signed main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); freopen("out.txt","w",stdout); #endif read(t); while(t--) { tot=0; memset(v,0,sizeof(v)); memset(id,0,sizeof(id)); memset(b,0,sizeof(b)); read(n); for(int i=1;i<=n;i++) { cin>>a[i]; if(a[i]=="nan") continue; int s=0; for(int j=0;j<a[i].size();j++) s=s*10+a[i][j]-'0'; b[++tot]=s,id[i]=b[tot]; } stable_sort(b+1,b+1+tot); int j=0; for(int i=1;i<=n;i++) { if(a[i]=="nan") { cout<<a[i]<<' '; continue; } else { if(j==tot||b[j]>id[i]) continue; while(++j) { if(b[j]) cout<<b[j]<<' '; if(b[j]==id[i]||j==tot) break; } } } cout<<endl; } }复杂度 \(O(n\log(n))\) ,带一定的常数(将字符串转换为整型)。
T3 混乱邪恶
点击查看题面

-
部分分:
-
\(97pts:\)
对,没看错,爆搜。
理解题面,显然 \(\sum\limits_{i=1}^n[c_i=1]a_i=\sum\limits_{i=1}^n[c_i=-1]a_i=\dfrac{sum}{2}\) ,其中 \(sum\) 表示 \(\sum\limits_{i=1}^{n}a_i\) 。
那么只需要爆搜使其满足上式即可。
先将 \(a\) 从小到大排序(不排 \(TLE~3\) 个点,从大到小 \(TLE\) 将近一半)。
玄学玩意儿。点击查看代码
#include<bits/stdc++.h> #define raed read #define ll long long #define endl '\n' using namespace std; const int N=1e6+10; template<typename Tp> inline void read(Tp&x) { x=0;register bool z=true; register char c=getchar(); for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0; for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); x=(z?x:~x+1); } int n,m; ll sum; bool is[N],dfn[N]; struct aa { int val,id; }a[N]; bool cmp(aa a,aa b) {return a.val<b.val;} bool dfs(int x) { if(sum==0) { dfn[x]=true; return true; } for(int i=x;i>=1;i--) { if(a[i].val>sum) continue; sum-=a[i].val; if(dfn[i-1]) { is[a[i].id]=true; dfn[x]=true; return true; } else if(dfs(i-1)) { is[a[i].id]=true; dfn[x]=true; return true; } sum+=a[i].val; } return false; } signed main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); freopen("out.txt","w",stdout); #endif read(n),read(m); for(int i=1;i<=n;i++) raed(a[i].val), a[i].id=i, sum+=a[i].val; stable_sort(a+1,a+1+n,cmp); sum>>=1; bool flag=dfs(n); if(sum!=0) { cout<<"Chaotic evil"; return 0; } cout<<"NP-Hard solved"<<endl; for(int i=1;i<=n;i++) if(is[i]) cout<<-1<<' '; else cout<<1<<' '; }我也不知道为啥这玩意儿能得 \(97\) ,数据得多水。复杂度不能用 \(n\) 来形容。为了卡常我甚至用了记忆化,但是没用。 -
\(0pts:\)
输出无解。
但是数据里没有无解。
根据他给的那个范围,无解的可能性极小,也可能没有,所以也正常。
-
-
正解(可能属于歪解):
既然他爆搜只有一个点过不去,那给他处理一下再爆搜不就能 \(AC\) 了。
对于他题面中给的限制,\(\{a_1,a_2,a_3,…,a_n\}\) 满足是 \(\{1,2,…,m\}\) 的子集,可以得出他满足 \(a_i-a_{i-1}\geq 1\) 。
所以先将 \(a\) 从小到大排序,这样能使 \(a_i-a_{i-1}\) 最小。
然后将其两两分组,组成新的 \(b\) 数组,\(b_{\frac{i}{2}}=a_i-a_{i-1}\) 。
那么至于 \(n\) 为奇数的情况,\(a[++n]=0\) 即可,最后输出的时候注意一下即可。
讲 \(b\) 也从小到大排序,和上面一样了。
这样再去爆搜 \(b\) ,和上面一样即可。
具体怎么处理看代码吧。
点击查看代码
#include<bits/stdc++.h> #define raed read #define int long long #define endl '\n' using namespace std; const int N=1e6+10; template<typename Tp> inline void read(Tp&x) { x=0;register bool z=true; register char c=getchar(); for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0; for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); x=(z?x:~x+1); } int n,m,sum; bool dfn[N],ss[N],f,is[N]; struct aa { int val,id; pair<int,int>dd; }a[N],b[N]; bool cmp(aa a,aa b) {return a.val<b.val;} bool dfs(int x) { if(sum==0) { dfn[x]=true; return true; } for(int i=x;i>=1;i--) { if(b[i].val>sum) continue; sum-=b[i].val; if(dfn[i-1]) { is[i]=true; dfn[x]=true; return true; } else if(dfs(i-1)) { is[i]=true; dfn[x]=true; return true; } sum+=b[i].val; } return false; } signed main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); freopen("out.txt","w",stdout); #endif read(n),read(m); if(n&1) f=1; for(int i=1;i<=n;i++) raed(a[i].val), a[i].id=i; if(n&1) a[++n].val=0; stable_sort(a+1,a+1+n,cmp); for(int i=1;i<=n;i++) if(i%2==0) b[i/2].val=a[i].val-a[i-1].val, b[i/2].dd=make_pair(a[i].id,a[i-1].id), sum+=b[i/2].val; stable_sort(b+1,b+1+n/2,cmp); sum>>=1; bool flag=dfs(n/2); if(sum!=0) { cout<<"Chaotic evil"; return 0; } cout<<"NP-Hard solved"<<endl; for(int i=1;i<=n/2;i++) if(is[i]) { int x=b[i].dd.first; ss[x]=true; } else { int y=b[i].dd.second; ss[y]=true; } for(int i=1;i<=(f?n-1:n);i++) if(ss[i]) cout<<-1<<' '; else cout<<1<<' '; }复杂度同样不能用 \(n\) 来形容。

