2024初三年后集训模拟测试4
前言

普及模拟赛,但是分拿的不高,主要想 \(T1\) 想时间太长了,别的没时间做了,时间分配有问题。
-
\(T1~100pts:\)
模拟+打表,立体的骰子不太容易想,规律也不好找,但发现规律后超级简单,我敢说我发现的规律是全机房最简便的。
但是想的时间用太长了,已经做出来了还验证半天。
题解写的详细写吧,好不容易想的。
-
\(T2~10pts:\)
贪心打假了。
-
\(T3~0pts:\)
赛时没时间了,赛后后悔死了,异常简单,所有数的欧拉函数乘起来就完事了。
-
\(T4~50pts:\)
背包 \(DP\) 会炸,\(10pts\) ,改成暴力 \(dfs\) \(O(2^n)\) ,也会超时 \(50pts\) 。
但是隔壁新任 剪枝教教主 @minecraft666 超级剪枝暴搜 \(100pts\) 。
数据有多水?超时的点全是 \(=m\) ,赛后加个 \(=m\) 直接输出的剪枝就 \(100pts\) 了 \(QWQ\) 。
T1 打赌
-
题意:
直接看吧:

注意这 \(4\) 个操作是循环进行的,直到最后一个点。

-
解法:
一眼大模拟,但是全交给电脑会 \(TLE\) ,\(n,m\leq 100000\) 。
考虑打表(找规律):
-
\(O(n)\) 解法:
显然在左右方向滚的时候,是 \(4\) 个一循环的,那么现在就是求对于每一行他的循环状态,设这个循环为 \(a_{1\sim 4}\)
每 \(4\) 个为一循环,每个循环的和为 \(14\) ,这是显然的。
不管如何,第一行肯定是 \(1,4,6,3,1,4……\) 循环的,要做的就是从当前行状态求出下一行状态。
-
先说结论,请看图:
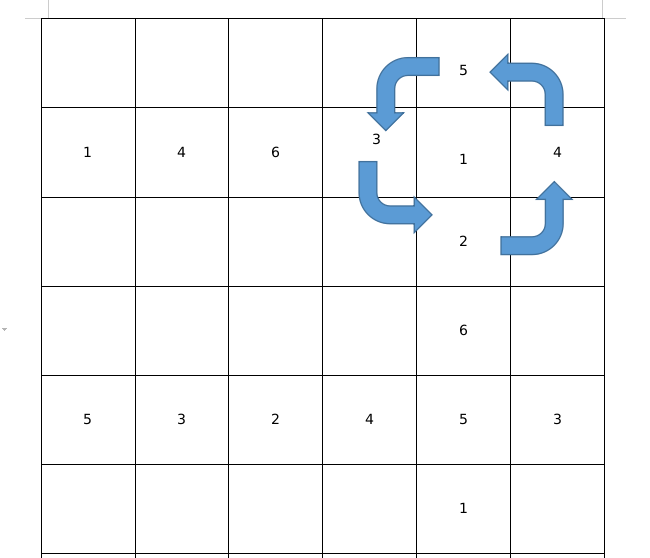
当前行最后处于上面的节点,也就是 \(a_{m\bmod 4}\) (视 \(0\) 作 \(4\) )这个点在当前循环的状态,在每一行的循环中,他的上下是固定的,也就是 \(5,2\) 这两个点。
以 \(1\) 这个点为例,若最后处于这个点,则下一行的循环状态为其 上,左,下,右 循环;当前点为下一循环的 下,其 上 为 \(7\) 减去当前点(相对两点相加为 \(7\) ) 。
设当前节点状态为 \(a_{now},c_1,c_2\) ,分别表示其循环、上和下;设下一层循环状态为 \(b_{1\sim 4},d_1,d_2\) 。
则有 \(b_1=c_1,b_2=a_{now-1},b_3=c_2,b_4=a_{now+1},c_2=a_{now},c_1=7-a_{now}\) 。
实际上就是该状态轮一圈,就是下一行的状态。
-
解析其正确性:
读题会发现在第 \(i\) 行时,若 \(i\) 为奇数是向右滚,反之向左滚,而前面却没有分类讨论。
在仔细思考题面发现,当 \(i\) 为奇数时,他的循环状态排列和正常平面图左右是相反的,如下图:
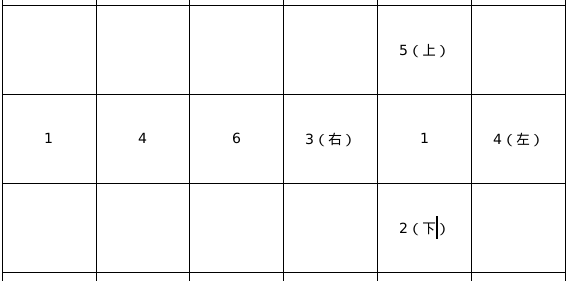
因为他是向右滚的,所以上一个滚到的显然是他的右侧,下一个滚到的为其左侧。
那么真实的情况就是:
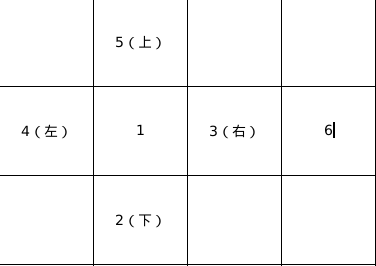
想象一下这个立体情景,那么他下一层的状态就应该是:
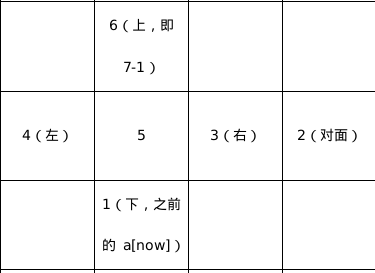
这次他要向左滚了,下一个点是他右边的点,那么他的循环就是 \(5,3,2,4\) 。
发现就成了我们上面的结论。
这是处理完了 \(i\) 为奇数的,\(i\) 为偶数同理的,只是将左右反过来,这次左右不反了,也是上面的结论。
-
最后实现:
直接按照结论来即可,注意 \(4\bmod 4=0\) 的问题,可以将 \(a\) 开成 \(0\sim 4\) ,\(a_0=a_4\) 。
点击查看代码
#include<bits/stdc++.h> #define int long long #define endl '\n' using namespace std; const int N=2e5+10; template<typename Tp> inline void read(Tp&x) { x=0;register bool z=1; register char c=getchar(); for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0; for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); x=(z?x:~x+1); } int n,m,a[5]={3,1,4,6,3},b[5],c[3]={0,5,2},x,ans; signed main() { // #ifndef ONLINE_JUDGE // freopen("in.txt","r",stdin); // freopen("out.txt","w",stdout); // #endif freopen("pogodak.in","r",stdin); freopen("pogodak.out","w",stdout); read(n),read(m); if(m%4==0) cout<<n*m/4*14,exit(0); int s=m/4,t=m%4; for(int i=1;i<=n;i++) { ans+=s*14; for(int j=1;j<=t;j++) ans+=a[j]; if(t==0) x=4; else x=t; b[1]=c[1],b[3]=c[2]; b[2]=a[x-1],b[0]=b[4]=a[(x+1)%4]; c[2]=a[x],c[1]=7-a[x]; for(int j=0;j<=4;j++) a[j]=b[j]; } cout<<ans; } -
-
\(O(1)\) 解法:
打表 。
他总共只有 \(m\bmod 4={0,1,2,3}\) 四种情况,为 \(0\) 时直接输出 \(n\times \dfrac{m}{4}\times 14\) 即可,就剩下三种。
直接用三种情况把上面三种情况在本地搞出来,把这个表交上去就可以了。
然后发现没什么意义,没比 \(O(n)\) 快多少甚至没有 \(O(n)\) 快,因为多处模运算常数巨大。
极其简单的,主函数里有用部分就 \(1\) 行。
点击查看代码
#include<bits/stdc++.h> #define int long long #define endl '\n' using namespace std; const int N=2e5+10; template<typename Tp> inline void read(Tp&x) { x=0;register bool z=1; register char c=getchar(); for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0; for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); x=(z?x:~x+1); } int n,m; const signed c[4]={1,4,6,2}, cas[4][6]= {0,0,0,0,0,0, 14,1,6,12,0,0, 42,5,11,19,28,36, 22,11,0,0,0,0}; signed main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); freopen("out.txt","w",stdout); #endif std::ios::sync_with_stdio(false); std::cin.tie(0);std::cout.tie(0); freopen("pogodak.in","r",stdin); freopen("pogodak.out","w",stdout); read(n),read(m); const signed ans=m%4; cout<<n*(m/4)*14+cas[ans][0]*(n/c[ans])+((n%c[ans]==0)?0:cas[ans][n%c[ans]]); }
-
T2 舞会
-
题意:
直接看吧:

-
部分分都是打假了的,没人尝试 \(O(n^2)\) ,没有整理的必要。
-
正解:
贪心
分成四个数组,分别为 低(想要)男,高男,低女,高女 的身高。设为 \(a_1,a_2,b_1,b_2\) 。
全部从小到大排序,\(a_1→b_2,a_2→b_1\) 分组。
双指针贪心即可,尽可能选择离自己身高最接近的舞伴。
时间复杂度 \(O(n)\) 。
直接看代码理解吧,有注释:
点击查看代码
#include<bits/stdc++.h> #define int long long #define endl '\n' using namespace std; const int N=1e5+10; template<typename Tp> inline void read(Tp&x) { x=0;register bool z=1; register char c=getchar(); for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0; for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); x=(z?x:~x+1); } int n,ans,girl1[N],girl2[N],boy1[N],boy2[N],cnt1,cnt2,tot1,tot2; bool v[N]; signed main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); freopen("out.txt","w",stdout); #endif freopen("party.in","r",stdin); freopen("party.out","w",stdout); read(n); for(int i=1;i<=n;i++) { int x; read(x); if(x<0) boy1[++tot1]=abs(x); else boy2[++tot2]=abs(x); } for(int i=1;i<=n;i++) { int x; read(x); if(x<0) girl1[++cnt1]=abs(x); else girl2[++cnt2]=abs(x); } stable_sort(boy1+1,boy1+1+tot1); stable_sort(boy2+1,boy2+1+tot2); stable_sort(girl1+1,girl1+1+cnt1); stable_sort(girl2+1,girl2+1+cnt2); for(int i=1,j=1;i<=tot1,j<=cnt2;i++,j++)//这里 i 也要 ++,上一个选他了这个就不能选他了。 { while(i<=tot1&&boy1[i]<=girl2[j]) i++; ans+=(i<=tot1);//从上面循环中跳出来的,一定是第一个(最近的一个)能配对的,如果一直到最后一个都不符合,那么跳出来的就是 tot1+1。 } for(int i=1,j=1;i<=tot2,j<=cnt1;i++,j++) { while(j<=cnt1&&boy2[i]>=girl1[j]) //同理,男女调换而已。 j++; ans+=(j<=cnt1); } cout<<ans; }
T3 最小生成树
-
题意:
\(n\) 个点构成完全图,每两点 \(i,j\) 间有且仅有一条边,边权为 \(\gcd(i,j)\) 。
现将其转换为最小生成树,要求父亲节点编号小于子节点,求方案数。
-
部分解:
\(40pts:\) 不开 \(long~long\) 。
-
正解:
欧拉函数 。
首先,\(1\) 与任何数 \(\gcd\) 均为 \(1\) ,所以将所有其他点都连到 \(1\) 就构成了最小生成树的一种情况。
那么由此,最小生成树要求所有边权为 \(1\) ,同时要求父亲节点小于子节点,恰好符合欧拉函数的定义。
求 \(\prod\limits_{i=1}^n\varphi(i)\) 即可。
可以线性筛出 \(1\sim n\) 的欧拉函数,时间复杂度 \(O(n)\) 。
点击查看代码
#include<bits/stdc++.h> #define int long long #define endl '\n' using namespace std; const int N=2e4+10,P=1e8+7; template<typename Tp> inline void read(Tp&x) { x=0;register bool z=1; register char c=getchar(); for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0; for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); x=(z?x:~x+1); } int n,phi[N],ans,len,prime[N]; bool vis[N]; void euler(int n) { phi[1]=1; for(int i=2;i<=n;i++) { if(!vis[i]) len++, prime[len]=i, phi[i]=i-1; for(int j=1;j<=len&&i*prime[j]<=n;j++) { vis[i*prime[j]]=1; if(!(i%prime[j])) { phi[i*prime[j]]=phi[i]*prime[j]; break; } else phi[i*prime[j]]=phi[i]*(prime[j]-1); } } } signed main() { // #ifndef ONLINE_JUDGE // freopen("in.txt","r",stdin); // freopen("out.txt","w",stdout); // #endif freopen("mst.in","r",stdin); freopen("mst.out","w",stdout); ans=1; read(n); euler(n); for(int i=1;i<=n;i++) ans=ans*phi[i]%P; cout<<ans; }
T4 买汽水
-
题意:
已知 \(a_{1\sim n}\) 和 \(m\) ,选取若干个相加使其和不大于 \(m\) 的情况下最大,求最大和。
-
部分分:
-
\(10pts:\)
背包 \(DP\) ,但是会炸空间和时间,题面数据范围给的不对差评。
-
\(50pts/60pts/70pts:\)
暴力 \(dfs\) 加剪枝,复杂度 \(O(2^n)\) ,正常是 \(50pts\) ,至于怎么超级剪枝请询问 @剪枝教教主 。
-
\(60pts:\)
输出 \(m\) ,对你没看错。
-
\(100pts:\)
歪解。
暴力 \(dfs\) 加剪枝加 \(sum=m\) 时直接输出 \(m\) 。
对,数据就是这么抽象。
-
-
正解:
双向搜索 ,又叫 折半搜索 ,官方名为 meet in middle 。
顾名思义拆成 \(1\sim \dfrac{n}{2},\dfrac{n}{2}+1\sim n\) 两部分进行搜索,在让他们两个相遇。
将第一遍搜索得到价值存到一个
set里,第二遍搜索得到的价值在set里面找满足 \(\leq m-sum\) (当前数量)的最大价值,进行转移即可。这样就将复杂度优化为 \(O(2^{\frac{n}{2}}\log(n))\) 。
点击查看代码
#include<bits/stdc++.h> #define int long long #define endl '\n' using namespace std; const int N=50; template<typename Tp> inline void read(Tp&x) { x=0;register bool z=1; register char c=getchar(); for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0; for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); x=(z?x:~x+1); } int n,m,sum,a[N],ans,f[N][2]; set<int>vis; void dfs(int x,int sum) { if(x>n/2) { if(sum<=m) vis.insert(sum); return ; } if(sum==m) cout<<m,exit(0); if(sum>m) return ; ans=max(ans,sum); if(sum+a[x]<=m) dfs(x+1,sum+a[x]); dfs(x+1,sum); } void dfsr(int x,int sum) { if(x>n) { if(sum<=m) ans=max(ans,sum+(*(--vis.upper_bound(m-sum)))); return ; } if(sum==m) cout<<m,exit(0); if(sum>m) return ; ans=max(ans,sum); if(sum+a[x]<=m) dfsr(x+1,sum+a[x]); dfsr(x+1,sum); } signed main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); freopen("out.txt","w",stdout); #endif freopen("drink.in","r",stdin); freopen("drink.out","w",stdout); read(n),read(m); for(int i=1;i<=n;i++) read(a[i]),sum+=a[i]; if(sum<=m) cout<<sum,exit(0); dfs(1,0); dfsr(n/2+1,0); cout<<ans; }
总结:
了解新知识——双向搜索。
教训:合理分配时间。
开题顺序不一定要挨着来,本次 \(T4→T2→T3→T1\) 最好。
要学会深入分析题面,如 \(T3\) 。
继续增强了大模拟和打表的能力,立体空间想象能力。

