求点双通分量及其缩点
概念
割点:对于一个无向图的点x,如果删去x后图不连通,则x为割点。
点双通分图:对于一个无向图,若其中不存在割点,则其为一个点双连通图。
点双通分量:对于一个无向图中的极大点双联通的子图,称这个子图为点双通分量 \((vDCCC)\)
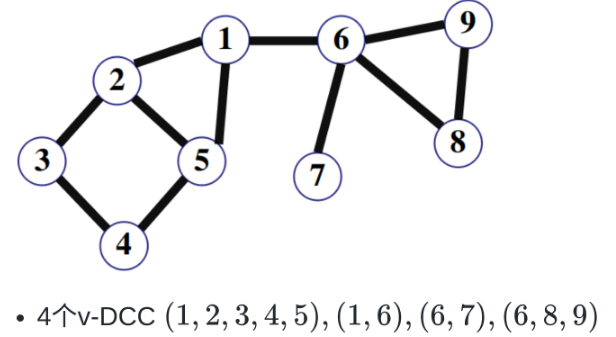
例如,如图,其中有4个 \(vDCCC\):{1,2,3,4},{5,6},{5,7,8},{1,5}(对割点要裂点)。
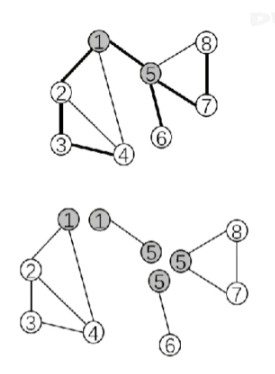
性质
- 除了一些比较特殊的点双,其他均满足:任意两点间都存在至少两条不重复路径。
比较特殊的点双:

- 任意一个割点(原图的割点)必定存在在两个点双中。
- 任意一个不是割点(原图的割点)的点必定只存在一个点双中。
tarjan算法求vDCC
用一个栈存点,当遍历回x时,发现割点判定法则 \(low[y]>=dfn[x]\) 成立,则从栈中弹出节点,直到y被弹出。
刚才弹出的节点和x一起构成一个vDCC。
代码实现
模板题:洛谷P8435 点双通分量
对于一个n个节点和m条无向边的图,请输出其点双通分量的个数,并描述每个点双通分量。
- 输入格式
第一行,两个整数n和m。
接下来m行,每行两个数a,b,表示一条无向边。 - 输出格式
第一行一个整数x表示点双通分量的个数。
接下来的x行,每行第一个数a表示该分量节点个数,然后a个数,描述一个点双通分量。
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=5e5+1;
vector<int>e[N],dcc[N];
int dfn[N],low[N],a,b,n,m,tot,num;
stack<int>s;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool f=1;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') f=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(f?x:~x+1);
}
void tarjan(int x,int fa)
{
dfn[x]=low[x]=++tot;
s.push(x);
if(x==fa&&e[x].size()==0)
{
dcc[++num].push_back(x);
return ;
}
for(int y:e[x])
if(!dfn[y])
{
tarjan(y,fa);
low[x]=min(low[x],low[y]);
if(low[y]>=dfn[x])
{
++num;
int z;
while(z!=y)
z=s.top(),
s.pop(),
dcc[num].push_back(z);
dcc[num].push_back(x);//与x共同构成一个vDCC
}
}
else low[x]=min(low[x],dfn[y]);
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(n),read(m);
while(m--)
read(a),read(b),
e[a].push_back(b),
e[b].push_back(a);
for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,i);
cout<<num<<endl;
for(int i=1;i<=num;i++)
{
cout<<dcc[i].size()<<' ';
for(int j=0;j<dcc[i].size();j++)
cout<<dcc[i][j]<<' ';
cout<<endl;
}
}
- 样例输入:
9 11
1 2
1 5
2 5
2 3
3 4
4 5
1 6
6 7
6 9
6 8
9 8 - 样例输出:
4
5 3 4 5 2 1
2 7 6
3 8 9 6
2 6 1
(第一个数是点双的数量,接下来每行第一个数是这个点双中点的数量,接下来描述这个点双)
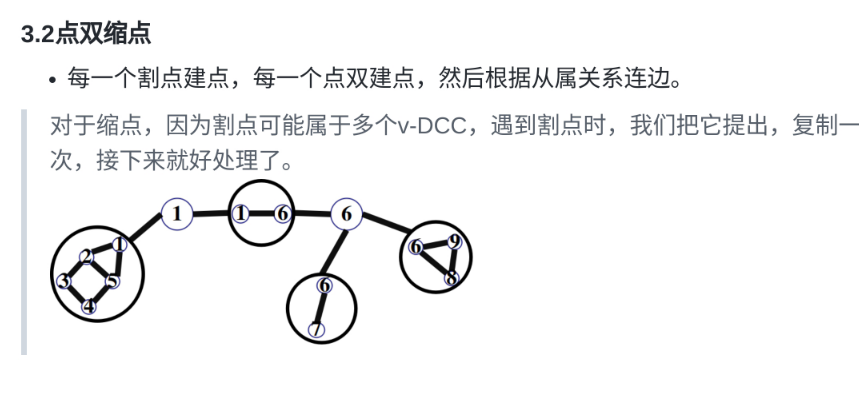
缩点
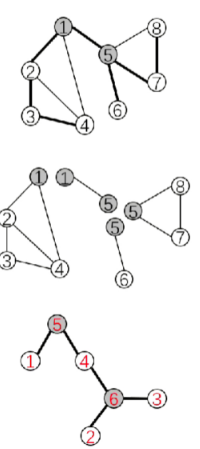

#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=5e5+1;
vector<int>e[N],dcc[N],ne[N];
int dfn[N],low[N],id[N],a,b,n,m,tot,num,cnt;
bool cut[N];
stack<int>s;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool f=1;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') f=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(f?x:~x+1);
}
void tarjan(int x,int fa)
{
dfn[x]=low[x]=++tot;
s.push(x);
if(x==fa&&e[x].size()==0)
{
dcc[++num].push_back(x);
return ;
}
int child=0;
for(int y:e[x])
if(!dfn[y])
{
tarjan(y,fa);
child++;
if(x!=fa||child>1) cut[x]=1;
low[x]=min(low[x],low[y]);
if(low[y]>=dfn[x])
{
++num;
int z;
while(z!=y)
z=s.top(),
s.pop(),
dcc[num].push_back(z);
dcc[num].push_back(x);//与x共同构成一个vDCC
}
}
else low[x]=min(low[x],dfn[y]);
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(n),read(m);
while(m--)
read(a),read(b),
e[a].push_back(b),
e[b].push_back(a);
for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,i);
cout<<num<<endl;
for(int i=1;i<=num;i++)
{
cout<<dcc[i].size()<<' ';
for(int j=0;j<dcc[i].size();j++)
cout<<dcc[i][j]<<' ';
cout<<endl;
}
for(int i=1;i<=n;i++) if(cut[i]) id[i]=++cnt;
for(int i=1;i<=num;i++)
for(int j=0;j<dcc[i].size();j++)
{
int x=dcc[i][j];
if(cut[x])
ne[i].push_back(id[x]),
ne[id[x]].push_back(i);
}
}
边双通分量
参考点双通分量,类似的。



\(懒得写了,oj里没有变双的题(确切地说唯一一道我用有向图打了qwq)\)

