蔬菜 2023
Tips
- 跑最短路时,dp 状态可以记在边上!
开路
数据结构开路
1. 依次被 \(i\sim n\) 操作 —— 分块前进技巧
现在有一个数 \(X\) 和一个序列 \(a_i\),想要维护 \(X\) 依次被 \(a_i,a_{i+1},\dots a_n\) 操作后的值,可以考虑将 \(a\) 序列分块,对每个块维护 \(x_i\) 当进来的 \(X\) 为 \(i\) 时出来的值将为 \(x_i\)。
2. 集合维护问题技巧 —— 分集合大小根号分治
考虑定一个阈值 \(B\),小的集合元素个数至多 \(O(B)\),可以直接枚举;大的集合至多有 \(O(n/B)\) 个,是可以始终维护这些大集合之间两两的信息的。
神秘猜结论开路
1. 根据合法数列数量猜结论
1.1 如果发现合法数列数量为 \(n!\),请想到将数列和排列构造一一对应!
数位 dp 开路
1. 每个 \(a_i\in [l_i,r_i]\) —— 维护极长不顶上下界连续段技巧
数位 dp 过程中,如果发现相邻两个数相同时最优,则可以设每个位置为 0/1/2 代表其 顶上界/顶下界/两者都不顶,于是极长 2 连续段的贡献由于可以任选易于计算, 于是记录 \(f(i,j,l,r,u)\) 表示 2 区间为 \([i,j]\),其中 \(i\) 位置高位情况为 \(l\),\(j\) 位置高位情况为 \(r\),当前位上右端点为 \(u\),进行转移。用区间 dp,每次将左边一段新区间和右边一段旧区间合并,时间复杂度 \(O(n^3\log V)\)。
树上问题开路
1. 树上二分改为 dfs 序上二分技巧
注意到任意一个 dfs 序都有一个性质:一个点的祖先一定在它的前面出现!
可以利用这个特点。例如,对于一个点来说,一段后缀 dfs 序中存在它的祖先 \(\iff\) 该后缀中存在它的父亲。
树形 dp 开路
1. 关于包含一个点的连通块性质 dp —— dfs 序前后缀背包合并技巧
考虑点分治,那么令 \(f(i,j)\) 表示 dfs 序在 \(u\) 前,选 \(j\) 个点的 dp 值,令 \(g(i,j)\) 表示 dfs 序在 \(u\) 后,选 \(j\) 个点的 dp 值,转移方程为 \(f_(i,j)\rightarrow f(i+siz_u,j)\) 以及 \(f_(i,j)\rightarrow f(i+1,j+1)\),前者表示 \(u\) 这个点及其子树都不选,后者表示至少选了 \(u\)。\(g\) 的转移需要被动转移,方程类似。注意这里 \(f\) 不考虑 \(u\) 的贡献,\(g\) 考虑 \(u\) 的贡献(而不钦定选或不选),因此对 \(u\) 计算答案时直接将背包 \(f\) 和 \(g\) 合并即可。
2. 基环树断边转树归入单根技巧
对于基环树上的 dp 问题,可以先随意断一条边,然后变成喜闻乐见的树上问题,随后没处理完的值都会归到根上,然后就只用考虑根一个点在环上转圈的问题了。
mex 相关 dp 开路
1. mex 值转移技巧 —— 维护值等价类
维护大于当前 \(mex\) 值的值等价类个数 \(k\),每次 \(mex\) 值 \(x\) 变化为 \(y\) 时,则乘上一个 \((y-x-1)!/k!\) 的贡献系数,表示在 \(k\) 个备选的等价类中选出 \(y-x-1\) 个置入。新增加一个数时,可以选择将其合并入一个等价类中或者新建一个等价类。
图论相关 dp 开路
1. \(\star\) 神秘图论题:图中删边技巧
对于神秘图论题(Loj3077绝目编诗),可以考虑分析性质,当 \(m-n\) 较大时直接得出结论,当 \(m-n\) 较小(小一个数量级)时,可以随意拉出一棵生成树,则非树边条数的级别为 \(m-n\),可以搞些有意思的东西。
各种操作开路
1. 树上操作:父亲维护儿子信息技巧 —— 每次对一个点进行操作
对每个点用个什么东西维护它与众儿子之间的关系,每次修改时直接根据维护的东西求得与儿子间的答案,父亲暴力更新。
2. 重复操作:允许重复对点进行操作时 —— 时间轴翻转有利于 dp
可以考虑将所有操作倒着做,这样可能使得一个点是在第一次被访问时贡献而非最后一次被访问时贡献,很有利于 dp!
3. 序列不断单点 +1,位运算相关:枚举最高变化位置
可以考虑枚举所有数中最高的有变化的位置 \(d\),发现该位置在变化后一定会使得 \(d\) 位以下都是 \(0\),于是方便下一步的考虑
构造题开路
1. 魔怔条件构造:随机小部分组成大部分技巧
对于神秘构造题(Uoj75智商锁),可以考虑先随出来若干个(最好较少以便 meet in the middle 快速计算扩展)小的部分,然后合并成大的部分。以此题为例,小部分的值域在 \([0,10^{12}]\) 左右时其 \(\bmod 998244353\) 的值可视为均匀随机,则选 4 个蜜桃猫乘起来即可。
2. 赋值类型操作技巧:倒过来做技巧
对于每次将一块局面变成统一性质的构造题,可以改为倒过来,每次选一块满足性质的块,倒过来会变成任意的块,会很好做。
变换条件开路
1. 数组中任取 \(k\) 个数之和 —— 全部减去最小值 \(mn\)
发现一个和 \(sum\) 对应着一个新的和 \(sum-k\times mn\),于是数组中出现了很多 \(0\),方便��理。
2. 和 \(\max,\min\) 有关的转化
- 考虑 \(0,1\) 转化!对于一个阈值 \(x\),\(\le x\) 的视为 \(0\),\(\ge x\) 的视为 \(1\)。
- 考虑差分!\(a_{i+2}>a_i\iff d_{i+1}+d_i>0\)。
优化
dp 优化
1. 区间 dp 决策单调性优化
对于一个 dp 过程 \(f(i,j)\),如果我们能证明 \(f(i,j)\) 的最优决策点 \(g(i,j)\) 满足 \(g(i-1,j)\le g(i,j)\le g(i,j+1)\),那么按区间长度排序处理,时间复杂度为 \(\sum\limits_{i,j} (g(i,j+1)-g(i-1,j))=\sum\limits_{len}m=O(m^2)\)。
2. 维护 dp 值域连续段技巧(dp 值域与定义域翻转技巧)
发现一个 dp 值 \(f_{i,j}\) 具有单调性且 \(f_{i,j}\) 的取值只有常数种,则可以改记 \(F_{i,c}\) 表示取值为 \(c\) 的 \(f_{i,j}\) 的 \(j\) 的区间。
图论优化
1. Dijikstra 相同边权点建虚点技巧
如果一张图中一个点 \(u\) 需要向若干个点连很多条边权相同的边,那么可以建一个虚点 \(w\),改为 \(u\) 向 \(w\) 连一条这个边权的边,然后视为 \(w\) 向这一堆点连边权为 \(0\) 的边,只把 \(w\) 塞进堆里。当将 \(w\) 弹出时,由于 \(w\) 连出的边边权均为 \(0\),因此 \(w\) 所连向的这些点可以不用塞进堆而是立即赋为 \(dis_w\) 并更新其他点。可以用数据结构加速找点的过程。
2. 交互题/通信题卡次数技巧
在我们运用人类智慧推出一车性质最终被卡 1~2 步次数时,一定要记得可以在小范围内使用 dp 进行决策! 往往较小的范围才会出问题,并且也省去了许多大力分讨的过程。
限制优化
1. 笛卡尔树上分治优化
如果题目要求对所有满足区间 \([l,r]\) 的最大值满足什么条件计数,那么可以对序列建一棵笛卡尔树,对于笛卡尔树上的每个区间,如果我们在处理的时候只用扫左半边和右半边的较短者,那么复杂度即为 \(O(n\log n)\)。
2. 上下界限制优化
关于一些奇怪的和式,可能值域和定义域都会有一些上界或下界,可以仔细观察式子,并将多余的上下界去除!(例如要求 \(\max_{i<j} h_i-i+h_j+j\le lim\) 等价于 \(\max_{i\neq j} h_i-i+h_j+j\le lim\))
时间复杂度证明
1. 基于势能观察的时间复杂度证明
尝试对一个东西进行不断的调整直至合法,可以考虑构造一个势能 \(\varphi\),每花 \(T\) 的时间该势能会减 \(\varphi\),则这个不断调整的时间复杂度至多为 \(\varphi\)。
1.(1) 区间分裂复杂度证明
如果对一个长度为 \(L\) 的区间进行若干次分裂为两个非空的区间,每次分裂时间复杂度为 \(O(1)\),那么即使最终可能有多个区间,时间复杂度仍为 \(O(L)\)。
1.(2) 上界降低复杂度证明
假设目前存在一个上界 \(lim\),每次有若干种决策,如果将上界降低 \(\Delta\) 所花时间为 \(O(\Delta)\),那么复杂度即为 \(O(lim)\)。
2. 块内线段树修改技巧
将序列分块后,可以对每个块分别建一棵线段树,节点上可以花 \(O(len)\) 的代价维护信息和合并儿子节点,对于块内单点修改,复杂度为 \(\sum\limits_{i\ge 0} \frac{B}{2^i}=O(B)\) 可以接受。(注意并不带 \(\log\)!)
3. 集合合并去重复杂度证明
有若干个集合,所有集合的大小之和为 \(V\),那么将所有集合逐渐合并时,每合并两个集合时,可以枚举小的集合里的元素(启发式合并 \(O(n\log n)\)),然后查询它是否在大集合里,如果在则减去这个交集,然后合并过去。容易发现每个元素至多被删除一次,于是这个复杂度总和是 \(O(V)\) 的。
计数
多项式科技
1. \(O(n^2)\) 相邻位置 dp 转移技巧
对于 \(f(i-1,j)\) 转移到 \(f(i,j-1),f(i,j),f(i,j+1)\) 的问题,可以将其转化成 $F\rightarrow F\cdot (ax+b+cx^{-1}) $ 的形式。发现最终的答案会形如 \(G_0F+G_1f_1[0]+G_2f_2[0]+\dots\) 的形式,其中 \(f_i[0]\) 表示第 \(i\) 次做完乘法之后的结果。考虑分治,计算每次乘完之后的 \(f[0]\) 然后再做一遍分治 NTT 即可。考虑计算区间 \([l,r]\) 中的答案,发现只有 \(x^{-(mid-l+1)}\dots x^{mid-l+1}\) 会对 \([l,mid]\) 中的 \(f[0]\) 产生影响。 于是可以拎出这部分的多项式递归下去处理,时间复杂度 \(O(n\log^2n)\)。尚未实现
构造
递归构造
1. 双重递归构造法
当我们希望构造出一个结构 \(A_n\),也许直接从 \(A_{n/2}\) 构造出 \(A_n\) 是困难的,此时我们可以考虑用人类智慧构造出一个 \(B_n\),然后 \(A_n\) 由 \(B_{n/2}\) 构造,\(B_n\) 由 \(A_{n/2}\) 构造,仍然是 \(\log\) 的。
证明成立
1. 证明图中不存在环的势能法
考虑对图 \(G\) 定义一个势能 \(\varphi(G)\),然后尝试证明如果 \(G\) 中存在环,那么令 \(G\) 以某种方式消环之后的结果为 \(G'\),并尝试证明 \(\varphi(G')<\varphi(G)\),如果成功,那么我们只需求出 \(\varphi(G)\) 最小的 \(G\) 即可。
建模
转化
1. 曼哈顿距离转切比雪夫距离技巧
将坐标 \((x,y)\) 转化为 \((x+y,x-y)\) 之后,原先的曼哈顿距离变为 \(\max (|x_1-x_2|,|y_1-y_2|)\),在最优化问题中,后者可以拆开,让每个点的贡献为 \(\pm x\) 或 \(\pm y\)。
2. 大小关系转 01 序列技巧
对于只和数与数之间的大小有关的序列及其操作题目,可以考虑枚举阈值 \(x\) 后转 01 序列并用数据结构维护。由于某个特定的 \(x<y\) 在转化后必然会在某个阈值时在 01 中显现出来, 因此这样做是对的。
3. 序列合并相邻两个数转二叉树技巧
将合并过程中每合并的两个数建立一个新节点,那整个过程就形成一个二叉树结构,可以通过二叉树上的 rotate 操作转化操作过程并证明最优性。
4. 区间排序后为等差数列转等差数列技巧
对于区间 \([l,r]\),若其中所有数 \(\bmod\ d\) 相同,且区间的 \(\max-\min=d\times (r-l)\),那么满足条件。
5. 排列/矩阵转二/三元组技巧(适用于逆排列操作的情况)
对于一个排列 \(p\),将其视为一个二元组的集合 \((i,p_i)\),那么对其取逆排列即为将集合中所有 \((x,y)\) 变为 \((y,x)\),即交换两维。
同理对于一个拉丁方阵,将其视为三元组集合 \((i,j,k)\) 代表第 \(i\) 行第 \(j\) 列的数为 \(k\),那么对每一行取逆排列即为 \((i,j,k)\rightarrow (k,j,i)\),对每一列取逆排列即为 \((i,j,k)\rightarrow (i,k,j)\),都是交换其中两维。
6. 凸性函数最小化和 转 函数差分技巧
考虑有很多个下凸函数 \(f_i(x)\),我们想求 \(\min\limits_{x_1+x_2+\dots x_k=s}\sum f_i(x)\),那么可以把它变成 \(\sum\limits_i\sum\limits_{k=1}^x (f_i(k)-f_i(k-1))\),于是取出前 \(s\) 大的差分值 \(f_i(k)-f_i(k-1)\) 即可!
组合意义
1. \((n-1)!!\Longrightarrow\) \(n\) 个元素两两配对的方案数
1.1 \(f(i,j)=f(i-1,j+1)+j\times f(i-1,j-1)\Longrightarrow\) 每次在括号序列末尾插一个左括号或插一个右括号并与左边一个左括号配对
2. 错排数 \(D_n=(n-1)(D_{n-1}+D_{n-2})\) 的另一种解释
考虑 \(n\) 个点的排列会形成若干个环,如果 \(n\) 所在的环长度大于 \(2\),那么删掉它后对应于 \(n-1\) 个点的错排环,重新插回来显然是 \(n-1\) 种方案;如果 \(n\) 所在的环长度等于 \(2\),那么删掉它会带走一个点,带走的那个点方案数也是 \(n-1\)。证毕。
网络流
1. 模拟费用流——中间一排点数较少
可以对于中间每两个点(以及源汇)之间维护一个优先队列表示所有边的权值 (由于这些点必然被经过),然后每次增广的时候只需要关心堆顶的边权的值,于是每次增广的复杂度是 \(O(1)\) 的(虽然常数有点大),然后将边反向的时候也最多改变 \(O(1)\) 次优先队列。
2. 若干物品每种物品选一种属性的技巧
最小割模型,从 \(S\) 到 \(T\) 拉出 \(n\) 条链代表 \(n\) 个物品,链的长度(边数)为 \(m\),断掉第 \(i\) 条链中的第 \(j\) 条边代表第 \(i\) 个物品选第 \(j\) 种属性。注意可以从 \((i,j)\) 向 \((i,j-1)\) 连一条 \(+\infty\) 流量的边防止一条链被断两次,详见 这里
3. 最小割模型由式子建边技巧
对于一种建模,可以列出许多 \(01\) 变量,注意每个代价形�� \(ax_i\),\(b\overline{x_i}\) 或 \(cx_i\overline{x_j}\),这样就可以对于每个变量 \(x_i\) 建一个点并处理 \(x_i\) 与 \(x_j\) 之间的连边了。
4. 每个点选黑色或白色,一个点的颜色受其它点限制贡献的技巧
以 BZOJ 3218 a+b problem 为例,每个黑点受是否在 \(S_i\) 中有白点而是否产生 \(p_i\) 的贡献。正确连边如下图所示,连 \(S\) 代表黑点,连 \(T\) 代表白点,题目求最大价值,因此答案为 \(W-\) 最小割:
分四类情况讨论:
- \(u\in S,u'\in S\):此时 \(p_u\) 不用割,因此产生 \(p_i\) 的贡献;
- \(u\in S,u'\in T\):此时 \(p_u\) 必须割,失去的 \(p_i\) 的贡献,注意此时边 \((u',u)\) 并不影响;
- \(u\in T,u'\in S\):此时由于 \((u',u)\) 的存在,不合法;
- \(u\in T,u'\in T\):此时 \(p_u\) 也必须割,失去的 \(p_i\) 的贡献。
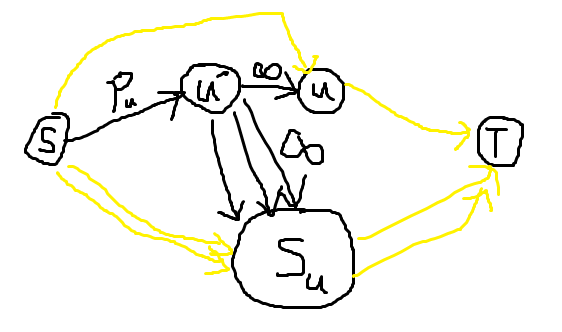
(如果一个黑点受 \(S_u\) 中是否有黑点而是否产生贡献,则可以考虑变成不用割 \((u',u)\) 会产生贡献,即代价为最小割而非 \(W-\) 最小割。)
5. 网络流边权解方程技巧
发现想用最小割而发现容量可能为负,或者想用最小费用最大流而发现费用无法确定,可以通过枚举所有情况并解方程得出每条边的正确边权。
例题:Uoj336 无限之环 要求旋转右边的水管使得整张图不漏水。

直接分类讨论,其中第一类要求中间的点拆成两个相对的各选一个,第三个 trivial,重点在第二个。
这个结果实际上是解方程解出来的,实现上可以所有流量 \(\times 3\) 即可:
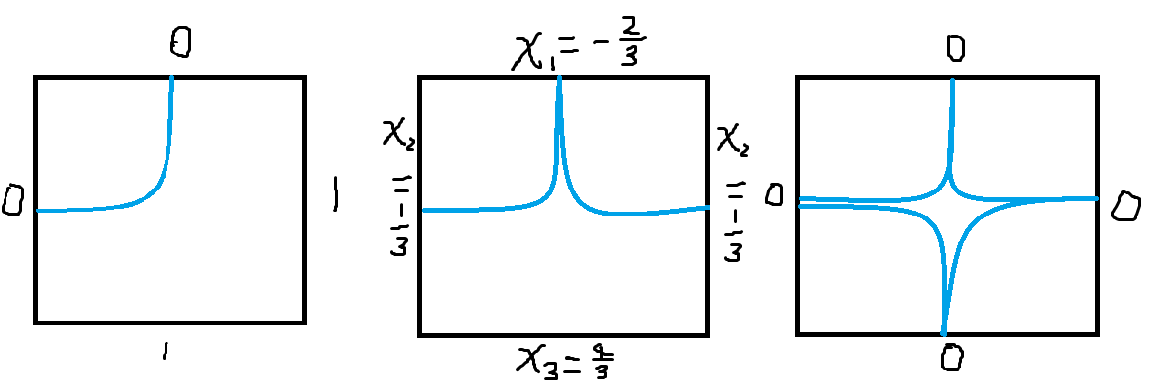
6. 链式最小割边权 \(+\infty\) 技巧
防止链式最小割出现负权边的一个有效方法是对图中所有点都加上一个很大的正无穷 \(W\),由于我们能够预知整张图的最小割大小一定为 \(n\),所以原图的最小割就是转化后的图的最小割加上 \(n\times W\)。注意这也是防止有一条链被割两次的一个方式!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号