Greedy
贪心整合包
Tricks
- 有些时候贪心是无法证明交换性的,一定要注意交换性是不是对的!即“我不要的你是否一定能拿到”
- 反悔贪心的用法:一个物品必然被某个人选,那么我们可以把它加进优先队列里,以后来人的时候再慢慢替换。
- 和区间有关的匹配可以用 Hall 定理很好地解释!
- Hall 定理求最大匹配是 \(|X|-\max(|S|-R(|S|))\),想求 \(\max(|S|-R(|S|))\),可以考虑求 \(R(|S|)\) 的补集的最大值,这样 \(\max\) 里面是加号,有利于处理。(你说得对,但是这本质上是不是最大流=最小割)
- 博弈中贪心选择的等价性:如果博弈的游戏有某种拓扑序上的限制(例如有向图,每次只能选一个零入度点),那我们可以考虑在假设没有这些限制下的最优决策,如果我们能够得出“最优决策双方的选择顺序符合原先限制”的结论,那这个博弈问题就可以等价成没有限制的问题来做了!
- 一边选一边有删除的问题一定要时间倒流,变成一边出现一边选,这个远远贪心 friendly 过原来的问题。
- 贪心的正确性不仅可以用于让时刻 \(t\) 的决策推到时刻 \(t+1\) 的决策,还可以用于让时刻 \(t+1\) 的决策倒推回时刻 \(t\) 的决策。
ARC076D Exhausted?
简要题意:有 \(n\) 个人 \(m\) 张椅子,第 \(i\) 个人只愿意坐在第 \(L_i\) 个椅子之前或第 \(R_i\) 个椅子之后,求至多有几个人坐下来。\(n,m\le 2\times 10^5,0\le L_i<R_i\le m+1\)。
Fake Solution
直接贪心,把所有人按 \(L_i\) 从小到大排序,\(L_i\) 相同的按 \(R_i\) 从大到小排序,然后贪心选,如果能放左边就放左边,否则放到右边的一个队列里面,左边放完之后再对右边排序处理。
Hack
3 4
1 3
2 5
2 5

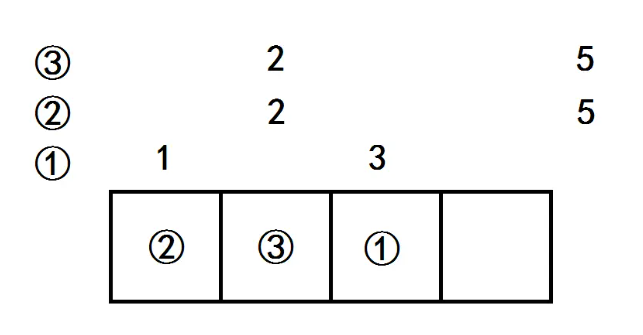
bigger:
12 10
6 7
0 9
5 10
0 9
2 5
3 9
2 8
3 10
6 7
5 9
4 9
3 9
Real Solution
为什么这种贪心是错的?因为我们想“证明”的交换性是错的。一开始想的“交换性”是基于“如果我的左端点靠前,那‘别人占我的位置,我拿其他位置’不如‘我占我的位置,别人拿那个其他位置’”,但是这是错的,因为“其他位置”别人不一定拿得到。没有正视这个漏洞而随手写了一发,居然过了,但是被题解区 hack 了。
做法一
还是要处理这种情况,可以考虑的一点是反悔贪心。事实上,我们之前的结论中有一点是正确的:我的这个位置,要么我占了,要么回头别人占了,一定不会空着。所以用反悔贪心来考虑,如果我有位置,我就暂时占着;如果我没位置了,那我就到前面去看看有没有适合抢的,如果有就抢一个,把多出来的那个塞到后面去。什么情况下“适合抢”呢?如果我的 \(R_i\) 要大于对方的 \(R_j\),那我确实更紧迫,留下我不如留下他,这个交换性是可以证的,所以我就可以把他换出来。剩下的右半部分照样处理。
做法二
这种问题可以被视为是最大匹配问题,可以尝试用 Hall 定理解决。Hall 定理有一个很有用的推论:最大匹配的大小为 \(|X|-\max(|S|-R(|S|))\)。对应到这道题上,我们要求最大匹配,就是要找出若干个集合,使(集合数量 - 它们的并的大小)最大,答案为 \(n\) 减去这个最大值。对于最大值中出现减号的问题,可以考虑将其取补集。所以变成最大化(集合数量 + 区间的交的大小),则发现区间的交可以偏小,所以枚举这个交集看有几个区间包含它即可。可以线段树优化到 \(O(n\log n)\)。
Fake Code
#include "bits/stdc++.h"
#ifdef DEBUG
#include "PrettyDebug.hpp"
#else
#define debug(...) [](auto...){}(__VA_ARGS__)
#define debuga(...) [](auto...){}(__VA_ARGS__)
#endif
#define For(i,a,b) for(int i=(a);i<=(b);i++)
#define Rev(i,a,b) for(int i=(a);i>=(b);i--)
#define Fin(file) freopen(file,"r",stdin)
#define Fout(file) freopen(file,"w",stdout)
#define assume(expr) ((!!(expr))||(exit((fprintf(stderr,"Assumption Failed: %s on Line %d\n",#expr,__LINE__),-1)),false))
#define fi first
#define se second
using namespace std; typedef long long ll; using pii = pair<int,int>;
constexpr int N=2e5+5;
int n,m; vector<int> lis[N]; priority_queue<int> q;
signed main(){
// Fin("hh.in");
atexit([](){cerr<<"Time = "<<clock()<<" ms"<<endl;});
cin>>n>>m; For(i,1,n) { int x,y; cin>>x>>y; lis[x].push_back(y); }
int ans=0,use=0; vector<int> vec; for(int u:lis[0]) vec.push_back(m-u+1);
For(x,1,m){
for(int u:lis[x]) q.push(u);
while(q.size()&&use<x) use++,q.pop();
while(q.size()) vec.push_back(m-q.top()+1),q.pop();
}
sort(vec.begin(),vec.end()); //debug(vec,use);
int lim=m-use; use=0; for(int x:vec) if(use<min(x,lim)) use++; else ans++;
cout<<ans<<'\n';
return 0;
}
// START TYPING IF YOU DON'T KNOW WHAT TO DO
// STOP TYPING IF YOU DON'T KNOW WHAT YOU'RE DOING
// CONTINUE, NON-STOPPING, FOR CHARLIEVINNIE
// Started Coding On: November 08 Wed, 07 : 51 : 25
Real Code(做法一)
#include "bits/stdc++.h"
#ifdef DEBUG
#include "PrettyDebug.hpp"
#else
#define debug(...) [](auto...){}(__VA_ARGS__)
#define debuga(...) [](auto...){}(__VA_ARGS__)
#endif
#define For(i,a,b) for(int i=(a);i<=(b);i++)
#define Rev(i,a,b) for(int i=(a);i>=(b);i--)
#define Fin(file) freopen(file,"r",stdin)
#define Fout(file) freopen(file,"w",stdout)
#define assume(expr) ((!!(expr))||(exit((fprintf(stderr,"Assumption Failed: %s on Line %d\n",#expr,__LINE__),-1)),false))
#define fi first
#define se second
using namespace std; typedef long long ll;
constexpr int N=2e5+5; using pii = pair<int,int>;
int n,m; pii a[N]; priority_queue<int,vector<int>,greater<>> q;
signed main(){
atexit([](){cerr<<"Time = "<<clock()<<" ms"<<endl;});
cin>>n>>m; For(i,1,n) cin>>a[i].fi>>a[i].se;
sort(a+1,a+1+n); int use=0; vector<int> vec;
For(i,1,n){
q.push(a[i].se);
if(use<a[i].fi) use++;
else vec.push_back(m-q.top()+1),q.pop();
}
int lim=m-use; use=0; int ans=0; sort(vec.begin(),vec.end()); debug(vec);
for(int x:vec) if(use<min(x,lim)) use++; else ans++;
cout<<ans<<'\n';
return 0;
}
// START TYPING IF YOU DON'T KNOW WHAT TO DO
// STOP TYPING IF YOU DON'T KNOW WHAT YOU'RE DOING
// CONTINUE, NON-STOPPING, FOR CHARLIEVINNIE
// Started Coding On: November 08 Wed, 09 : 01 : 49
暴力&gen(对拍用)
#include "bits/stdc++.h"
#ifdef DEBUG
#include "PrettyDebug.hpp"
#else
#define debug(...) [](auto...){}(__VA_ARGS__)
#define debuga(...) [](auto...){}(__VA_ARGS__)
#endif
#define For(i,a,b) for(int i=(a);i<=(b);i++)
#define Rev(i,a,b) for(int i=(a);i>=(b);i--)
#define Fin(file) freopen(file,"r",stdin)
#define Fout(file) freopen(file,"w",stdout)
#define assume(expr) ((!!(expr))||(exit((fprintf(stderr,"Assumption Failed: %s on Line %d\n",#expr,__LINE__),-1)),false))
using namespace std; typedef long long ll;
constexpr int N=15;
int n,m,L[N],R[N],ans,vis[N];
void dfs(int u,int res){
if(res>ans) return;
if(u==n+1) return ans=min(ans,res),void();
For(i,1,L[u]) if(!vis[i]){
vis[i]=1; dfs(u+1,res); vis[i]=0;
}
For(i,R[u],m) if(!vis[i]){
vis[i]=1; dfs(u+1,res); vis[i]=0;
}
dfs(u+1,res+1);
}
signed main(){
atexit([](){cerr<<"Time = "<<clock()<<" ms"<<endl;});
cin>>n>>m; For(i,1,n) cin>>L[i]>>R[i];
ans=1e9; dfs(1,0); cout<<ans<<'\n';
return 0;
}
// START TYPING IF YOU DON'T KNOW WHAT TO DO
// STOP TYPING IF YOU DON'T KNOW WHAT YOU'RE DOING
// CONTINUE, NON-STOPPING, FOR CHARLIEVINNIE
// Started Coding On: November 08 Wed, 08 : 22 : 39
#include "bits/stdc++.h"
#ifdef DEBUG
#include "PrettyDebug.hpp"
#else
#define debug(...) [](auto...){}(__VA_ARGS__)
#define debuga(...) [](auto...){}(__VA_ARGS__)
#endif
#define For(i,a,b) for(int i=(a);i<=(b);i++)
#define Rev(i,a,b) for(int i=(a);i>=(b);i--)
#define Fin(file) freopen(file,"r",stdin)
#define Fout(file) freopen(file,"w",stdout)
#define assume(expr) ((!!(expr))||(exit((fprintf(stderr,"Assumption Failed: %s on Line %d\n",#expr,__LINE__),-1)),false))
using namespace std; typedef long long ll;
mt19937 rng(chrono::high_resolution_clock::now().time_since_epoch().count());
long long rnd(ll l,ll r) { return uniform_int_distribution<ll>(l,r)(rng); }
void rnd(long long& l,long long& r,long long n) { l=rnd(1,n); r=rnd(1,n); if(l>r) swap(l,r); }
void rnd(int& l,int& r,int n) { l=rnd(1,n); r=rnd(1,n); if(l>r) swap(l,r); }
signed main(){
atexit([](){cerr<<"Time = "<<clock()<<" ms"<<endl;});
int n=12,m=10; cout<<n<<' '<<m<<'\n';
For(i,1,n) { int l=0,r=0; while(l==r) l=rnd(0,m+1),r=rnd(0,m+1);; if(l>r) swap(l,r);; cout<<l<<' '<<r<<'\n'; }
return 0;
}
// START TYPING IF YOU DON'T KNOW WHAT TO DO
// STOP TYPING IF YOU DON'T KNOW WHAT YOU'RE DOING
// CONTINUE, NON-STOPPING, FOR CHARLIEVINNIE
// Started Coding On: November 08 Wed, 08 : 24 : 38
CF725F Family Photos
简要题意:Alice 和 Bonnie 玩游戏,有 \(n\) 堆相片,每堆两张,必须选了上面那张才能选下面的,每张对 Alice 有一个价值 \(a_i\),对 Bonnie 有一个价值 \(b_i\)。双方轮流选照片,可以 pass,当双方都 pass 的时候结束。双方都只想最大化(自己的价值 - 对方的价值)。求结果。\(n\le 10^5\)。
Solution
想得有点晕,去看题解了。这类问题好像最好的办法就是看看 \(a,b,a+b,a-b,ab,a/b\) 之类的比比大小。但是怎么看呢?模拟一下思路吧。
首先大致可以想到这里的“价值”大致是 \(a+b\),所以应该可以猜到要拿 \(a_i+b_i\) 比大小。
对于一对相片 \((a_i,b_i,a_j,b_j)\),分讨 \(a_i+b_i\) 和 \(a_j+b_j\) 的大小关系:
若只有 \(a_i+b_i\ge a_j+b_j\) 的相片对,则 \(a_i-b_j\ge a_j-b_i\),所以如果两张不可兼得,Alice 会希望拿第一张;\(b_i-a_j\ge b_j-a_i\),所以如果两张不可兼得,Bonnie 也会希望拿第一张。
怎么定义“希望”?如果我们能自由选择先拿哪一张的话,我们也会选择先拿第一张!因此,如果只有这一类相片对,那我们可以把这个游戏等价成将每对相片拆开,大家随意选,因为即使让大家随意选,大家也会遵守原先的规则。而对于这个新的等价的游戏,双方最优策略显然是直接按顺序贪心选最大的。
若存在 \(a_i+b_i<a_j+b_j\) 的相片对,则 \(a_i-b_j<a_j-b_i\) 且 \(b_i-a_j<b_j-a_i\),所以双方都不愿意选第一张。这样前面拆开的方式就不成立了。但是从另一个角度入手,可以发现若 \(a_i-b_j>0\),则 \(b_i-a_j<0<a_i-b_j\),因此 Alice 不用担心 Bonnie 抢这对相片(因为这太亏了),所以 Alice 完全可以放到最后再选;同理若 \(b_i-a_j>0\) Bonnie 也可以放到最后再选。若两者都小于等于 \(0\),那双方都选了不如不选(不存在破坏对方的必要),所以这对相片就没用。
综上,对于 \(a_i+b_i<a_j+b_j\) 的相片对,要么没用,要么有利方可以留到最后再选,对面无论如何不可能破坏;对于 \(a_i+b_i\ge a_j+b_j\) 的相片对,可以等价于把每对相片拆开,可以排序后迅速计算。那这道题就做完了。
点击查看代码
#include "bits/stdc++.h"
#ifdef DEBUG
#include "PrettyDebug.hpp"
#else
#define debug(...) [](auto...){}(__VA_ARGS__)
#define debuga(...) [](auto...){}(__VA_ARGS__)
#endif
#define For(i,a,b) for(int i=(a);i<=(b);i++)
#define Rev(i,a,b) for(int i=(a);i>=(b);i--)
#define Fin(file) freopen(file,"r",stdin)
#define Fout(file) freopen(file,"w",stdout)
#define assume(expr) ((!!(expr))||(exit((fprintf(stderr,"Assumption Failed: %s on Line %d\n",#expr,__LINE__),-1)),false))
using namespace std; typedef long long ll;
constexpr int N=1e5+5;
int n;
signed main(){
atexit([](){cerr<<"Time = "<<clock()<<" ms"<<endl;});
cin>>n; vector<tuple<int,int,int>> lis; ll ans=0;
For(i,1,n){
int a1,b1,a2,b2; cin>>a1>>b1>>a2>>b2;
if(a1+b1>=a2+b2) lis.emplace_back(a1+b1,a1,b1),lis.emplace_back(a2+b2,a2,b2);
else{
if(a1>b2) ans+=a1-b2;
else if(b1>a2) ans+=a2-b1;
}
}
sort(lis.begin(),lis.end(),greater<>()); int O=0;
for(auto [_,a,b]:lis){
O^=1; if(O==1) ans+=a; else ans-=b;
}
cout<<ans<<'\n';
return 0;
}
// START TYPING IF YOU DON'T KNOW WHAT TO DO
// STOP TYPING IF YOU DON'T KNOW WHAT YOU'RE DOING
// CONTINUE, NON-STOPPING, FOR CHARLIEVINNIE
// Started Coding On: November 08 Wed, 11 : 08 : 22
AGC023F 01 on Tree
Too 典,略过。
有一个遗留问题:每棵子树的最优决策是整棵树的最优决策的一个子序列,但是这一点显然吗?由整道题的解法容易证出,但是有别的方法吗?
Loj3366 [IOI2020] 嘉年华奖券
Too easy,略过。
AGC007F Shik and Copying String
难点不在贪心。略过。
Loj2306 「NOI2017」蔬菜
简要题意:有 \(n\) 种蔬菜,第 \(i\) 种蔬菜单棵价值 \(a_i\),共有 \(c_i\) 棵,被(几乎)平均分为 \(\lceil c_i/x_i \rceil\) 批,第 \(j\) 批有 \(x_i\) 个(除了最后一批)且会在第 \(j+1\) 天过期。你每天可以卖出至多 \(m\) 棵没过期的蔬菜,并且当你第一次卖出第 \(i\) 种蔬菜的时候会有 \(s_i\) 的政府补贴。有 \(Q\) 次询问,每次询问给你 \(p_i\) 天时间能得到的最大收益。\(n,Q\le 10^5,m\le 10\)。
Solution
这是一个有关删除的问题,可以考虑时光倒流。这个开局想不到就寄了。
时光倒流,变成每个时刻会出现 \(x_i\) 棵蔬菜,那贪心策略很显然,就是选当前存在的最大的 \(m\) 个即可。这个贪心策略在时光倒流的情况下是显然的,但是为什么正着做很别扭呢?大概这就是删除的困难所在吧。用堆随便贪心维护一下就行了。
进一步,我们考虑多组询问怎么处理。发现很关键的一点性质:卖 \(p-1\) 天的答案可以由卖 \(p\) 天的答案推得,方式就是从 \(p\) 天的答案中扔掉价值最小的 \(m\) 棵蔬菜。为什么这是对的呢?因为在前 \(p\) 天中能卖的蔬菜,前 \(p-1\) 天肯定也能卖;如果前 \(p\) 天卖的蔬菜不包含前 \(p-1\) 的最优解,那大概可以把前 \(p\) 天中除了最后一天卖的东西去替换前 \(p-1\) 天的策略得到更优的解。所以直接对 \(p=10^5\) 求出答案,然后把过程中卖的所有菜从大到小排序即可。
cmd 采用了模拟费用流的方式做这道题,但是感觉有牛刀杀鸡之嫌,绕了挺多圈。当然可能赛场上脑子不清醒的时候用模拟费用流来做可以省去一些弯路。
这道题还有一个神奇的地方:我们的第一个猜测是前 \(p\) 天的决策是基于前 \(p-1\) 天的基础上的,但是这是错误的,样例就是反例;但是却可以证明前 \(p\) 天卖的总共的蔬菜一定是前 \(p-1\) 天卖的总共的蔬菜的超集。很神秘。
Code
#include "bits/stdc++.h"
#ifdef DEBUG
#include "PrettyDebug.hpp"
#else
#define debug(...) [](auto...){}(__VA_ARGS__)
#define debuga(...) [](auto...){}(__VA_ARGS__)
#endif
#define For(i,a,b) for(int i=(a);i<=(b);i++)
#define Rev(i,a,b) for(int i=(a);i>=(b);i--)
#define Fin(file) freopen(file,"r",stdin)
#define Fout(file) freopen(file,"w",stdout)
#define assume(expr) ((!!(expr))||(exit((fprintf(stderr,"Assumption Failed: %s on Line %d\n",#expr,__LINE__),-1)),false))
using namespace std; typedef long long ll;
constexpr int N=1e5+5,Z=1e5;
int n,m,Q,a[N],s[N],c[N],X[N],tim[N],vis[N]; vector<int> lis[N]; priority_queue<pair<int,int>> q;
signed main(){
// Fin("hh.in"); //Fout("hh.out");
atexit([](){cerr<<"Time = "<<clock()<<" ms"<<endl;}); ios::sync_with_stdio(0); cin.tie(0);
cin>>n>>m>>Q;
For(i,1,n){
cin>>a[i]>>s[i]>>c[i]>>X[i];
if(X[i]==0) lis[Z].push_back(i);
else{
tim[i]=c[i]/X[i]; lis[tim[i]+1].push_back(i);
}
}
vector<ll> ans;
Rev(id,Z,1){
vector<int> tmp;
for(int u:lis[id]){
if(X[u]==0) q.emplace(s[u]+a[u],u);
else{
if(c[u]%X[u]==0) tmp.push_back(u);
else q.emplace(s[u]+a[u],u);
}
}
For(_,1,m){
if(q.empty()) { ans.push_back(0); continue; }
auto [x,u]=q.top(); q.pop(); ans.push_back(x); vis[u]=1; debug(id,_,x);
if(--c[u]>0){
if(c[u]>X[u]*(id-1)) q.emplace(a[u],u); else tmp.push_back(u);
}
}
sort(tmp.begin(),tmp.end()); tmp.erase(unique(tmp.begin(),tmp.end()),tmp.end());
for(int u:tmp) {
if(!vis[u]) q.emplace(s[u]+a[u],u); else q.emplace(a[u],u);
}
}
sort(ans.begin(),ans.end(),greater<>()); partial_sum(ans.begin(),ans.end(),ans.begin());
while(Q--){
int x; cin>>x; cout<<(x==0?0:ans[x*m-1])<<'\n';
}
return 0;
}
// START TYPING IF YOU DON'T KNOW WHAT TO DO
// STOP TYPING IF YOU DON'T KNOW WHAT YOU'RE DOING
// CONTINUE, NON-STOPPING, FOR CHARLIEVINNIE
// Started Coding On: November 08 Wed, 19 : 57 : 59


 浙公网安备 33010602011771号
浙公网安备 33010602011771号