Lectures
\(\dagger\) Copy and Paste 3（P9523）
Problem
Solution
- 转移方程中的“父问题枚举子问题寻找转移”可以转成“子问题寻找父问题主动转移”处理
Goldfish and pikes（qoj1249）
Problem
Solution
- “大鱼吃小鱼”的题目，必然考虑值域倍增的性质
- “不断操作直至停止”的题目，考虑通过性质将操作分段，每段中有较好的性质（如为一区间等）
Easy Jump（gym103687E）
Problem
Solution
- 如果有大致的贪心策略，形如某种情况下用第一种策略，其余情况用第二种，则可以二分/枚举这个阈值进行处理
Student's Camp（CF708E）
Problem
Solution
- 要求区间相交时的容斥技巧：区间必须相交不好刻画，条件较多；但是区间不交很好刻画：\(r_a<l_b\) 或 \(r_b<l_a\)，至多有一个成立，因此可以很好地容斥。
老虎.机（P9379）
Problem
Solution
- “多次询问同一贪心过程得到的结果”的题目，可以考虑计算出每一条转移边（而不是点）的贡献，然后对每次询问，只用统计每条边贡献的系数即可。
Subset（gym103428B）
Problem
Solution
- 反演思想：如果通过 \(f\) 的方案数能推出 \(g\) 的方案数，则若转移矩阵可逆，则 \(g\) 的方案数也能推出 \(f\) 的方案数。说起来挺蠢的，但是容斥是可以这样解释的。下次到底用 \(-1\) 的几次方不好理解的时候就这样想吧。不过反演思想除了对容斥起作用也可以在类似这样的题里起作用：选出集合 \(\rightarrow\)（乘上阶乘）\(\rightarrow\) 选出不可重序列 \(\rightarrow\)（用性质映射）\(\rightarrow\) 选出可重序列 \(\rightarrow\) dp 处理
Alice、Bob 与 DFS（loj3633）
Problem
Solution
- SG 函数的拓展：SG 函数是可以定义在集合上的，所以如果我们规定的游戏是“\(i\) 可以转移到 \(\{R_i\}\) 或集合 \(S\)”，则可以把它变成在 \(\mathbb{N}\setminus S\) 上的游戏“\(i\) 可以转移到 \(\{R_i\}\)”，然后在这个集合上用 SG 定理，此时用于异或的值应该是第 \(k\) 小中的 \(k\)。
\(\dagger\) Just Kingdom (CF1578J)
Problem
Solution
- 形如“一个初始状态至少要多大，才能使末状态满足条件”的题，可以考虑倒推。很多题都要想到倒推。
- 对于“不断操作，每次加上 \(\max(A_i,B_i)\)”之类的问题，一定要记得值域倍增的技巧，只考虑值域没有倍增的情况如何快速转移！（上面的吃鱼题系列也都是这种技巧）
Wall Painting (PTZ winter 2020 Day2 C, Qoj1189)
Problem
Solution
- 关于线段覆盖最优化的题目，似乎要么是可以证明区间互不包含最优（此时可以扫右端点维护左端点处理），要么可以证明区间不部分相交最优（此时区间之间的关系形成一棵树）。立个 flag，以后注意看看是不是区间题都是这样的。
Square Constraints (AGC036F)
Problem
Solution
- 关于排列的 dp 问题，主要是两种形式：一种是相对大小的限制，一种是上界的限制。前者我们主要用的是按值域插入的方式，几乎别无良法；后者我们主要用的是 \(\prod (A_i-i+1)\) 的方式，也几乎别无良法。这道题显然属于后者，所以我们只能考虑 \(\prod (A_i-i+1)\)。为此我们必须将上界进行排序，同时我们对下界毫无办法，所以我们必须容斥，于是下界就变成了上界，题目就可做了。事实上这个思路可能应该是必然的，因为面对这样的问题我们应该没有别的路。
Cupboards Jumps (CF1500F)
Problem
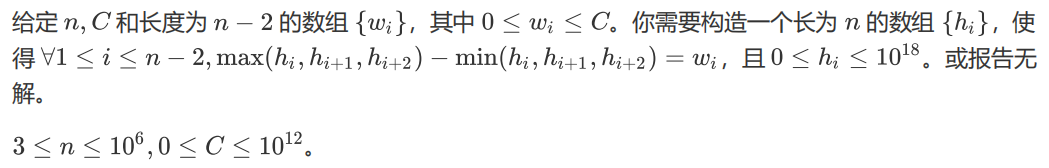
Solution
- 非常典的题，技巧就是先求出一种比较简单清晰的 dp 形式，然后尝试用
set维护 dp 值，如果整个 dp 都形如 \(f_{x,i}\rightarrow f_{x+1,i+j}\) 之类的良好形式，则可以很好地用 set 打标记转移。
Tenzing and Random Operations (CF1842G)
Problem
Solution
- 拆括号的技巧。当遇到 \(\prod a_i\) 的期望的时候，可以考虑拆括号，然后计算括号中的每一项出现的概率。
\(\dagger\) 1st ucup stage 20 E Strange Keyboard
Problem
Solution
- 字典树上所有子树的叶子个数之和是 \(O(\sum |s_i|)\) 的，这是一个有用的结论，值得记下来。
- 同余最短路也有很深刻的性质：我们只关心边的集合而不关心走的顺序！所以同余最短路可以做到 \(O(nm)\)，其中 \(n\) 为环长，\(m\) 为不同的边权数量。写法为沿着环推两遍即可。
2nd ucup stage 6 K Jump Graph
Problem
Solution
- 关于这样的“两两之间的权值”的问题，注意一定要能够倒过来思考。例如这题，题面是“\(u\) 到所有点的距离和”，要想到把这个权值倒过来，考虑每个点对每个 \(u\) 贡献多少，然后发现这个贡献的形式很好。所以我们可以将这个贡献改成由 \(v\) 节点给 \(u\) 节点贡献，可以发现这样的贡献形式要好很多，是形如一个不断扩张的区间的形式，因此这道题就可以通过不断跳区间解决。
2nd ucup stage 6 B The Doubling Game 2
Problem
Solution
- 在树上的随机选顺序的问题，
