【计数,DP】CF1081G Mergesort Strikes Back
现有一归并排序算法,但是算法很天才,设了个递归深度上限,如果递归深度到达 \(k\) 则立即返回。其它部分都和正常归并排序一样,递归中点是 \(\lfloor (l+r)/2 \rfloor\),归并每次取两边较小者加入结果。
给定 \(n,k\),求用这个算法对一个均匀随机的排列 \(p\) 排序后,\(p\) 的期望逆序对数是多少,答案对输入的质数取模。\(n,k\le 10^5\)。
技巧:\(\prod 1/\mathrm{siz}_u\)
首先注意到其实就是把那一车长度为 \(n/2^k\) 左右的区间同时拿来归并。
仔细想一想会发现如果选了一个数,它的下一个数比它小,那一定会跟着选下一个数。推下去可以发现就是每个区间的前缀最大值带着一串小兵一起以前缀最大值为关键字排序。
这道题是求“和的期望”,所以自然应该想到拆贡献。考虑两个位置 \(x,y\) 之间产生贡献的期望值是多少。
如果 \(x,y\) 在同一段区间,那由于同一段区间内相对顺序不变(前缀最大值递增),所以 \(x,y\) 为逆序对的概率即为 \(1/2\)。
如果 \(x,y\) 在不同区间,设 \(x\) 所在区间长度为 \(a\),\(y\) 所在区间长度为 \(b\),则贡献期望值显然只和 \(a,b\) 有关。又 \(a,b\) 只有两种取值,外层直接枚举即可。
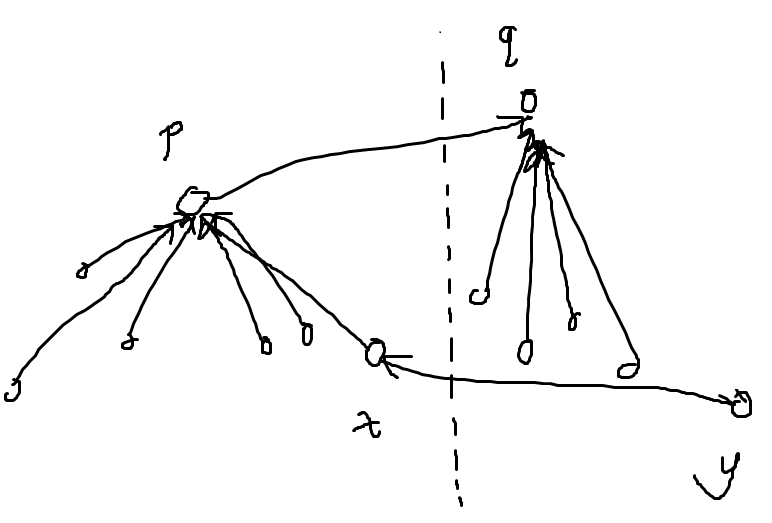
现在 \(a,b\) 固定了。考虑钦定 \(x\) 在 \(y\) 前面构成逆序对的条件,设 \(x\) 左边的第一个前缀最大值为 \(p\),\(y\) 左边的第一个前缀最大值为 \(q\),则成立的充要条件为:\(B_y<A_x<A_p<B_q,\forall 1\le i<x,A_i<A_p,\forall 1\le j<y,B_j<B_q\)。其它位置可以随便填,无关紧要,这是这种做法正确的基础。
发现我们刚才需要成立的关系形成一棵树!根据经典结论,所有关系都成立的概率为 \(\prod 1/\mathrm{siz}_u\),其中 \(\mathrm{siz}_u\) 表示 \(u\) 的子树大小。
把暴力写出来,是 \(O(ab)\) 的。再推一推发现可以预处理倒数的前缀和优化,就线性了。
注意特判 \(p=x\) 的情况。
点击查看代码
#include <bits/stdc++.h>
#define For(i,a,b) for(int i=a;i<=b;i++)
#define Rev(i,a,b) for(int i=a;i>=b;i--)
#define Fin(file) freopen(file,"r",stdin);
#define Fout(file) freopen(file,"w",stdout);
using namespace std;
const int N=1e5+5; using ll = long long;
int n,K,mod,inv[N],si[N];
int work(int a,int b){
int res=0;
For(i,1,a){
int tt=(b-1-1ll*(i+1)*(si[i+b]-si[i+1]+mod)%mod+mod)%mod;
res=(res+(1ll*inv[2]*(i-1)+1)%mod*inv[i+1]%mod*tt)%mod;
}
return res;
}
int main(){
cin>>n>>K>>mod; K--; K=min(K,18);
inv[1]=1; For(i,2,n+1) inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
For(i,1,n+1) si[i]=(si[i-1]+inv[i])%mod;
int a=n>>K,b=a+1,cb=n-(a<<K),ca=(1<<K)-cb;
int ans=(1ll*a*(a-1)/2%mod*ca+1ll*b*(b-1)/2%mod*cb)%mod*inv[2]%mod;
ans=(ans+1ll*ca*(ca-1)%mod*work(a,a))%mod;
ans=(ans+1ll*cb*(cb-1)%mod*work(b,b))%mod;
ans=(ans+1ll*ca*cb%mod*work(a,b))%mod;
ans=(ans+1ll*cb*ca%mod*work(b,a))%mod;
cout<<ans<<'\n';
return 0;
}



