ARC129E Yet Another Minimization 题解 【网络流笔记】

Link
超神的建模，极其有借鉴意义/cy
注：该建模对应于最小割建模

对于 \(n\) 个数，每个数有 \(m\) 种取值的技巧

\(\forall i=1,2,\dots,n\)，令 \(S=V_{i,0}\rightarrow V_{i,1}\rightarrow \dots \rightarrow V_{i,m}=T\)，也就是形成 \(n\) 条链。
此时，\(i\) 取值 \(j\) 时对应着切断边 \(V_{i,j-1}\rightarrow V_{i,j}\)，因此这条边可以附上权值 \(c_{i,j}\)。
注意，这时候我们还要连一条 \(V_{i,j}\rightarrow V_{i,j-1}\) 的边，边权为 \(+\infty\)。理由如下：

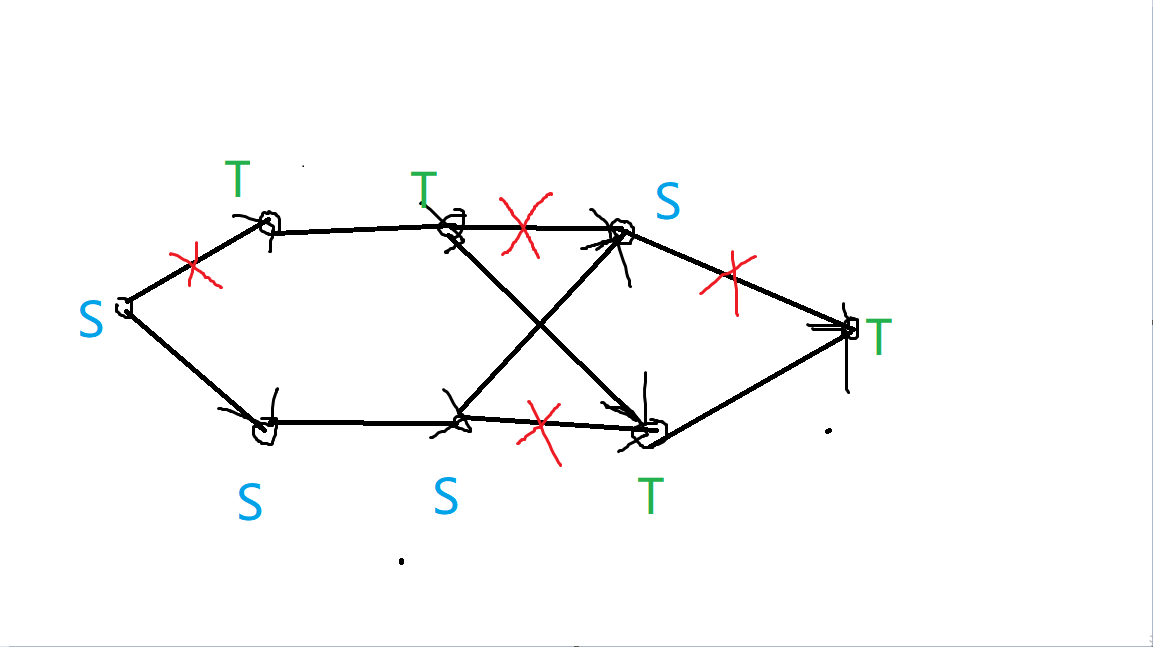
我们会发现上面那条链断了 3 条边，由于有其它边的介入，左边跑到 \(T\) 一边了，右边跑到 \(S\) 一边了，这显然不符合我们的期望。

而加上无穷大的边后————

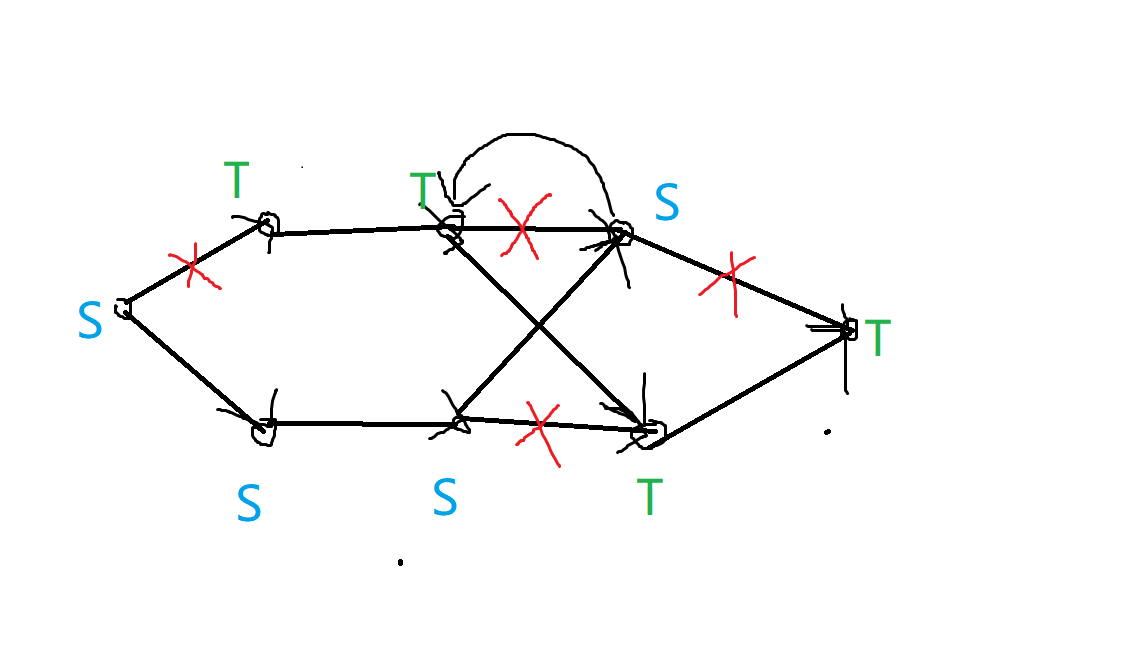
发现 \(S\) 和 \(T\) 连通了，显然与最小割不符。于是可以保证每条链左边属于 \(S\)，右边属于 \(T\)。

另外，如果一条链断了 3 条边，则 3 条小链中必有两个同属于 \(S\) 或 \(T\)，它们之间的边就没必要断了，与最小性不符。

至此，我们可以保证每条链恰好断一条边，其代价对应于选相应元素的代价，且左边属于 \(S\)，右边属于 \(T\)。

处理不同数所选值之间关系的技巧

本题中要求对于数 \(i\) 和 \(j\)，会产生 \(|x_i-x_j|\cdot W_{i,j}\) 的代价。

不妨设 \(x_i<x_j\)（反之类似），则代价即为 \(\sum\limits_a [x_i\le a<x_j] W_{i,j}\)。

于是考虑对每个 \(a\) 连一条代价为 \(W_{i,j}\) 的边。

对 \(x_i,x_j\) 进行归并排序，则相邻两个数之间的 \(a\) 可以合并，于是只有 \(O(m)\) 条边。

举一个 \(x_i\le a<x_j\) 的例子：

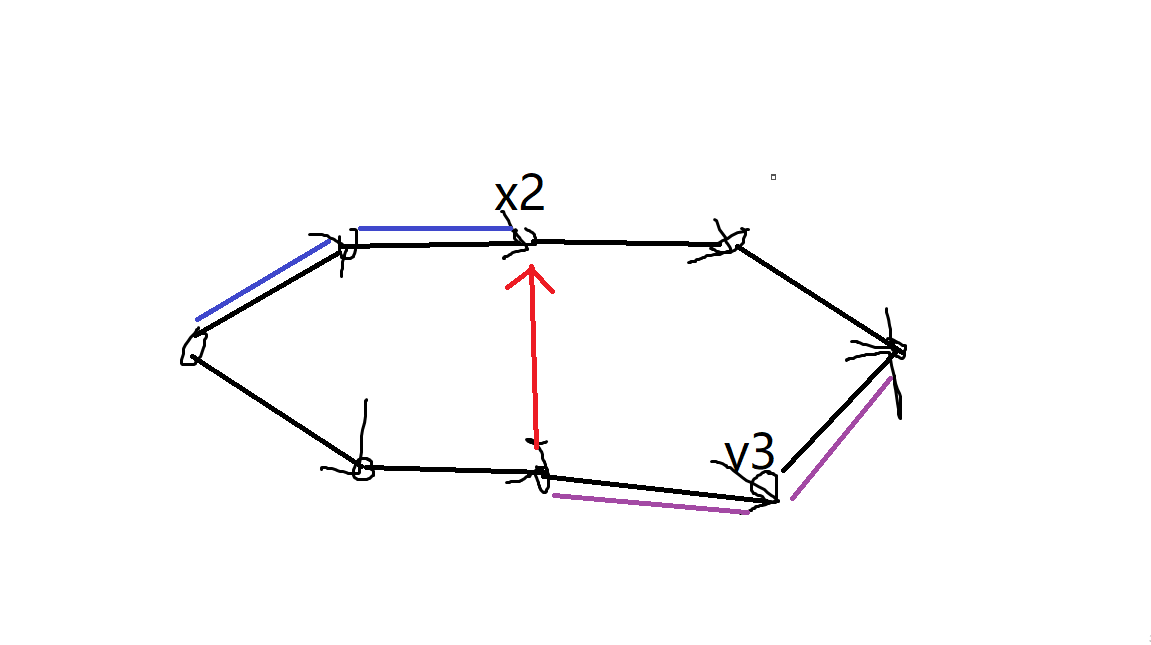
可以看到图中 \(x_2<y_3\)，即 \(x_2\le a<y_3\)，此时上面那条链可以切蓝色的边，下面那条链可以切紫色的边，于是此时是从 \(y_2\) 向 \(x_2\) 连一条边，边权为 \(y_3-x_2\)。

注意一下谁往谁连边即可，注意权值差也有可能是 \(x_k-x_{k-1}\)，需要取一个 \(\max\)。