蔬菜专题
公式
- $ \sum \binom{2j}{j} \binom{2i-2j}{2j}=4^i $
- $ \prod[w_i=1]={1\over 2^n} \sum\limits_S \Big( \prod\limits_{j\in S}w_j \Big) \ (w_i=\pm1) $
- $ FWT(f)=g \Longleftrightarrow g_S=\sum\limits_T (-1)^{|S \cap T|}f_T $ 可以倒着用
- $ \prod {1\over 1-a_iz} = \sum c_i{1\over 1-a_iz} \Longleftrightarrow c_i={1\over \prod\limits_{j\neq i}(1-{a_j \over a_i})} $
建模
一个 01 序列区间的众数 = 将 0 换成 -1 后区间和与 0 的关系
ARC137E:覆盖一个区间,每个位置覆盖次数有上限,超过后无贡献:最小费用循环流模型
在一个 DAG 中删去一些点,使剩下任意 3 个点不在一条链上:将原图 G 复制一遍得到 G',对于每个点 u,从 G 中的 u 向 G' 中的 u 连边。答案即为这个新图的最长反链=最小路径点覆盖(=二分图匹配)。
一个合法的点分树,设它的根权值为树的深度,每个点的权值为其父节点的权值 -1,那么点分树方案合法 <=> 任意两个权值相同的点之间有一个权值比它们大的点
思想
每当 pos 右移一位时,a 只有一个元素性质发生大的改变,其它元素平移后不变/变化相同
求“aaa中xxx的最大值”的最大值,可以枚举 aaa 中的所有 xxx,使它最大,记录下结果,再在所有结果中取最大值
边很稀疏的图 ($m-n \le 9$ 之类的)可以考虑收缩 1,2 度点,甚至收缩 3 度点进行递归求解
Segment Tree Beats: 留坑。。。
当对一个序列的操作等与其元素之间的大小有关时,可以考虑将 $\le k$ 的视为 $0$,$>k$ 的视为 $1$,01 串的操作往往有一些很好的性质
对于一些作用在多个(复杂)位置的操作,可以考虑用数据结构(一般是线段树)维护操作轴即时间轴,然后按顺序枚举位置(而不是时间)
从一个字符串 $S$ 加/删 字符变成另一个字符串 $T$,可以考虑将操作倒过来,变成从 $T$ 删/加 字符变成 $S$,往往会取得奇效
区间放一个数查询区间 mex:
1. 区间内连续出现最远的 → 区间取反,变为区间内“每个位置最小出现”的最大值 (貌似这是 mex 题的常见套路)
2. 标记永久化:$\max(\min(lc,v),\min(rc,v))=\min(v,\max(lc,rc))$
AC 自动机能够处理:$O(\log len)$ 求出一堆串中拎出一个文本串,其它串作为模式串出现的次数(路径 +1 fail 树求和)—— fail 树是一个可以与 SAM 媲美的东西
动态规划肯定要排序,但不一定要从左到右转移,也可以将所有转移排序,然后一个个转移进行,这样可以保证转移过程中的另一个有序性(如凸包上的斜率)。此时假的转移自然就假了,真的转移一定能转
技巧
$mod 2$ 意义下的多项式,乘法(又称二项卷积)可以变为子集卷积,求逆即为自身,可以各种乱搞
当一个区间的答案与其最小值/最大值有关时,可以考虑对整个序列建出笛卡尔树,然后对每个节点预处理出其前后缀的答案,对于每组询问 $[l,r]$,以其最大值/最小值 $k$ 为中心划分成三部分:$val(l,r),f(l,k-1),f(k+1,r)$ 计算,后两者即为一个节点的前缀/后缀
分治 FFT 只需要保证递归层数是 $O(\log n)$ 级别的,例如 $m$ 个多项式相乘,次数和为 $n$,尽管这些多项式次数各不相同,但直接普通分治 FFT,每层的次数和均为 $O(n)$,共 $O(\log n)$ 层,则总复杂度为 $O(n \log^2 n)$
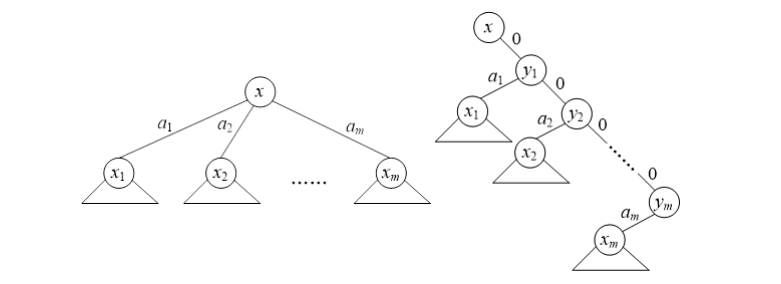
!! 有些(很多)换根树形 dp 可以对于每个“上子树”都算出它的 dp 值,但这样做是 $O(n^2)$ 的(虽然界很弱),怎么办?拆点!将一个点的若干个儿子拆成一条链(和边分治一样),然后就是 $O(n)$ 的了(边权的重赋值可能有点棘手)
求强连通分量中所有环长度的 $\gcd$,可以跑出一棵 dfs 树,然后对所有非树边 $(i,j)$,求 $|dep_i+1-dep_j|$ 的 $\gcd$。
——对于一些传染性问题的技巧——
1. 如果转移是直至无穷时候的并且是循环的,那么可以每次不同时转移,而是每次只转移一步
2. 初始时每个点找出一条出边,找不到一般很平凡,否则就成了一棵基环树。
3. 转移的性质有时满足:若 a -> b,那么 a 一定比 b 劣。这时,可以从每棵基环树开始搜,搜到其它基环树则并查集合并,否则只遇到自己,自己就是答案。
4. 运用 Boruvka 算法的复杂度分析,我们每次对于一层中所有基环树同时开搜,这样每轮基环树个数至少减半,于是就是 $O(n \log n)$ 的。
—————————————————
对于一棵树,求一棵子树内是否有某种颜色,可以将所有有此颜色的点按 dfs 序排序,每个点打标记 +1,每相邻两个点的 lca 打标记 -1,答案即为子树内标记和
(因为听说 pb 在 GDOI2019 因为不会这个技巧爆炸了所以全部加粗)
dp 神奇优化:CDQ 分治(?,$solve(l,r)$ 递归到 $solve(l,k-1)$ 与 $solve(k,r)$,在中间处理 $[l,k-1]$ 到 $[k,r]$ 的转移。
然后 $k$ 不一定要是区间中点,如果能够在 $\min (k-l,r-k)$ 的时间内处理出这个转移,则时间复杂度等同于启发式合并,$O(n \log n)$。
复杂度分析:有时一个算法的复杂度可能看上去是 $O(nmk)$ 的,实际上是 $O(nk\frac{m}{k})$ 的,然后你就过了(?
如果要求一个区间第 $k$ 大的数的贡献,可以转为枚举每个位置,看它在那些区间里面是第 $k$ 大,这个就开一个链表,每次查询最小的左右两边 $k$ 个位置,再把它删掉。
解树上的 dp 方程的好套路:$f_u=\sum\limits_{v \in son_u} c_vf_v+d_uf_{fa_u}$,则记 $f_u=a_uf_{fa_u}+b_u$,当 $u$ 为根时就有 $f_u=b_u$,于是再从上到下递推回来即可
处理点分树的技巧:留坑
对于一个由若干条直线组成的下凸函数,可以用如下方法求出它的所有拐点:先找出最左端和最右段的直线,找出它们的交点,如果这个交点在凸壳上,则这个区间内只有这一个拐点,返回;否则,找到这个交点横坐标所在直线,左右递归处理。这个过程是 $O(n)$ 的(不会证)
若 $a_1,a_2,\dots,a_n$ 中有 $k$ 个子集的和为 $j$,则不妨设 $a_1+a_2+\dots+a_x=j$,有 $a_1,a_2,\dots,a_x,-a_{x+1},-a_{x+2},\dots,-a_n$ 中有 $k$ 个子集的和为 $0$。
公式2
当 $B,C$ 中的元素值都是 $v$ 时,可以双重递推计算
$ \det \begin{pmatrix} A & B \\ C & D \end{pmatrix} $ 与 $ \det_s \begin{pmatrix} A & B \\ C & D \end{pmatrix} $
(递推到 $ \det A, \det_s A, \det D, \det_s D $ )。
其中 $\det_s A$ 代表将 $A$ 中任意一行全变成 $1$ 之后求和。具体递推方式见 https://www.cnblogs.com/PYWBKTDA/p/15909123.html
重点在于计算将 $A$ 中所有数都减去 $t$ 之后的矩阵 $A_t$ 的 $\det$ 与 $\det_s$ 值。
实现
当计算中可能出现 0 的逆元时,可以考虑定义整数类 Int,存储结果为 $x \cdot p^y$
将整个 bitset 翻转(不是01反转)过来,可以先用 to_string 转化成字符串,字符串翻过来,再转化回去(不过是 $O(n)$ 的)
当数组需要负数下标时,可以先找出所有负数的最小值,然后将偏移量设为这个最小值的相反数(而不是事先定义,会浪费很多空间)


