寒假集训随笔

一个很有用的树上离线技巧

给定一批询问 $(u,k)$，问的是一棵树上某个点 $u$ 的 $k$ 级祖先是什么。

怎么办？把所有询问离线下来，把询问 $(u,k)$ 塞进 $u$ 的一个 vector 里面，然后对整棵树进行 dfs，维护一个数组 $dis[i]$ 表示从当前节点到根的路径上，深度为 $i$ 的节点与根节点的距离。

然后询问的答案就是 $curdis-dis[dep[u]-k]$。

超稠密二分图求最大匹配

其实就是说只有 $m$ 条边不在边集里面。

将点分成两类：度数（即这 $m$ 条边的度数） $\leq \sqrt{m}$ 的点和 $> \sqrt{m}$ 的点。

首先将第一类点直接寻找匹配，就是直接枚举每个右部点看能不能匹配，不能就丢到第二类。

然后将第二类点暴力 dfs 匹配。注意 dfs 时记录一个数组 fa 表示下一个未访问的右部节点，使用 for(int v=getfa(u+1);v!=n+1;v=getfa(v+1)) 来枚举 v，否则大力爆炸！！

时间复杂度 $O(n\sqrt{m})$。

神建模1：括号序列->二叉树

将 (A)B 对应到左儿子为 A，右儿子为 B，对付括号序列的神奇变换很有用

神建模2：数字序列->树

当看见一个序列满足 $f(i)\leq i$ 或 $f(i)\geq i$ 时，一定一定要条件反射地想到树qwq

神建模3：01序列-> < > 序列

详见这里，说也说不清，太神了（

核心思想：往一个01序列添加0/1->把一个0换成01或把一个1换成01，做到不重不漏

树上二维 DP 玄学优化

定理：由 $1$ 和 $-1$ 组成的随机序列前缀和绝对值最大值期望为 $O(\sqrt{n})$ 的，于是可以将所有儿子随机排列后进行转移，数组第二维只用开到 $O(\sqrt{n})$

容斥枚举所有 $(x,y)$ 使得 $n|xy$

这里我们可以对于任意 $(a,b)$，迅速求出所有 $(x,y)$ 使得 $a|x,b|y$，设这个集合为 $f(a,b)$。

考虑 $n=p^{\alpha}$ 时，答案为 $\sum\limits_{i=0}^{\alpha} f(p^i,p^{\alpha-i})-\sum\limits_{i=0}^{\alpha-1} f(p^{i+1},p^{\alpha-i})$ （注意求和上界不同）

证明：$f(p^i,p^{\alpha-i})-f(p^{i+1},p^{\alpha-i})$ 就是当 $\gcd(x,n)=p^i$ 时，枚举 $\gcd(y,n)$ 中 $p$ 的次数 $\geq \alpha-i$。

对于任意 $n$，则对于 $n$ 的每个质因子 $p_i$ 都进行上述计算，在 dfs 的过程中维护系数即可。（注意到 $f$ 可以算是“积性”的）

关键的，时间复杂度与下列等价：（枚举所有 $n$ 的因数）*（2^{$n$ 的质因子个数}）= $O(\sigma^2(n))$ ！

附上个图：

 

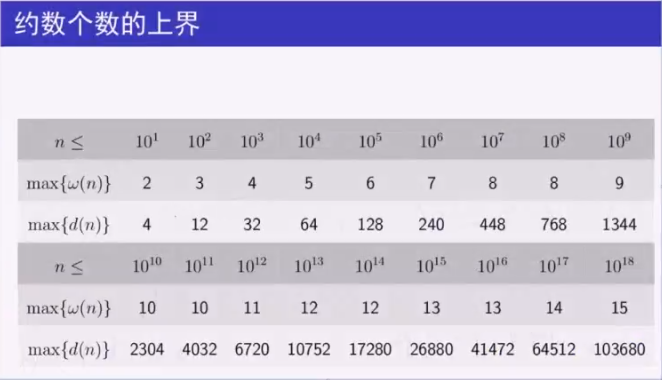
 所以，这个算法足以处理 $n \leq 10^{11}$ 的情况！

容斥的技巧

1~n 至少出现一个 → 1~n 都不出现

x 最早出现的位置 <=k → x 在 1~k 都不出现

二分图的力量

二分图最大匹配 = 二分图最小点覆盖 = 2n - 二分图最大独立集 = n - DAG 最小路径点覆盖

倒过来：

DAG 最小路径点覆盖 = 二分图最大独立集 - n，于是可以变成特殊图求最大独立集

猜测的力量

很多题往往可以猜一个结论（通常是猜最优情况），然后通过构造证明出可以达到这个最优情况。无论是传统题还是构造题均有效。

如何正确应用最大流-最小割定理

一般都是跑最大流来求出最小割对吧

太肤浅了！！！

很多网络流神题都是求最大流→求最小割（而不是反过来）！通过最小割分析性质，再回来求最大流！