12.3 杂题选讲
【HDU 5451/计蒜客A1988】 Best Solver
对于模 $p$ 的二维递推数列 $a_n=ua_{n-1}+va_{n-2}$ 来说,有“扩展费马小定理”:$(x,y)$ 有循环节 $p^2-1$。
为什么呢?所有 $[x,y](x \neq 0,y \neq 0)$ 与所有 $[x,y]\begin{pmatrix}{{1,u}\\{0,v}}\end{pmatrix}(x \neq 0,y \neq 0)$ 形成一一对应,得证。
于是对于 $a[2^x (x \leq 2^32)]$ 来说,快速幂求 $y=2^x \mod p^2-1$ 然后再矩阵快速幂求 $f^y$ 即可。
【Codeforces 356E】Xenia and String Problem
1. 后缀数组很好用。
用来 $O(1)$ 求任意两个后缀的 lcp($O(n \log n)$ 预处理)。
要敲熟,否则考场上调傻。
2. 类似于“若区间满足xx条件,则贡献加 $x$,求修改至多一个位置后总贡献最大值”的问题。
枚举所有区间(如果可以的话),区间中每个数标记加 $x$(用差分)。
然后再枚举所有区间,计算哪些位置修改了之后可以使得这个区间产生贡献多少。
最后对每个位置取 $\max$ 即可。
【Codeforces Gym 100221C】Forbidden Subwords
AC自动机上两端无限合法串计数。
两端无限意味着:1. 任意一个强连通分量是一个简单环(或一个点) 2.任意一条路径上至多有3个环
于是合法路径只能是一个环经过若干个点到另一个环。
dp 即可。
SG函数的妙用。算法的转化。非常神奇。
发现这是贪心之后又发现这不就是博弈的一个 dp 过程吗?
然后反过来用SG函数即可。
性质:若一个有向无环图有 $m$ 条边,则其 SG 函数值至多为 $\sqrt{2m}$。
证明:当每个点都往后所有点连边时最大,证毕(
所以朴素求 $mex$ 不要犯傻,这玩意不是 n 方,是 $O(m)$ 的。。。
【Codeforces 641F】Little Artem and 2-SAT
学会如何多次 dfs 求 2-SAT 问题的解。
注意如果 $n$ 较小($\leq 1 \times 10^3$),可以用 bitset 求传递闭包然后计算。
重要技巧:摩尔投票法
假设有 $n$ 个人参与投票,一人一票。选出所有至少得 $\frac{n}{k}$ 票的人,可以容错(满足条件的一定要选,不满足条件的也可以选,但共至多选出 $k$ 个)
办法:每次找出 $k+1$ 个意见各不相同的人,让他们打一架互相抵消,最后剩下 $k$ 个满足条件。
证明:显然人多势众总能把少数党压下去。
应用时 $k$ 较小则可以尽管用线段树维护 $k$ 个人。
【AtCoder ARC070 D】HonestOrUnkind
同样用摩尔投票法hhh
主要思想就是 A 说 B 是假人,辨认不出?宁杀错不放过,一起丢掉(
由于老实人一定要比假人多,总有老实人剩下。
【CodeChef SUMDIS】Sum of distances
分治+偏序。
注意维护 $\sum\limits_{\max(x_i,y_i) \leq 0} \max(x_i,y_i)$ 可以分解成 $\sum\limits_{x_i \leq y_i \leq 0} y_i$ 和 $\sum\limits_{y_i < x_i) \leq 0} x_i$ 分别维护就行啦~ (注意前面是 $\leq$ 而后面是 $<$)
【CodeChef WALKBT】Walks on the binary tree
定理:树上 $k$ 个节点构成的虚树,假设它们按 dfs 序排序为 $c_1,c_2,\dots,c_k$,则虚树大小为 $dis(c_1,c_2)+dis(c_2,c_3)+\dots+dis(c_{k-1},c_k)+dis(c_k+c_1)$。
重要技巧:用主席树维护序列。
养成习惯,change() 返回一个新的根,调用时用 root[cnt]=T.change(root[cnt],1,n,x,y) ,这样可以避免在需要多次赋值而不更新副本时无意义地增加节点数量。
重要技巧2:在主席树上求两个序列的字典序大小/lcp。
二分前缀判断 hash 是否相等?$O(n \log^2 n)$,太 low 了。
直接定义一个 $lcp(x,y,l,r)$,判断是否有 $hash(lc_x)=hash(lc_y)$,若是则返回 $mid-l+1+lcp(rc_x,rc_y,mid+1,r)$,否则返回 $lcp(lc_x,lc_y,l,mid)$。$O(n \log n)$ 搞定。
定理:对于方程 $\forall i=1,2,\dots,n, f_i=\max(a_i,\frac{f_{i-1}+f_{i+1}}{2})$(即左右随机游走的最大期望收益)。
它的解法是:对于坐标系上的 $n+1$ 个点 $(0,f_0=0),(1,f_1),(2,f_2),\dots,(n,f_n),(n+1,f_{n+1}=0)$,求这些点的凸包,则凸包上的点是“停止点”,其它点的最优解在左右相邻两个停止点的连线上。
如图所示:
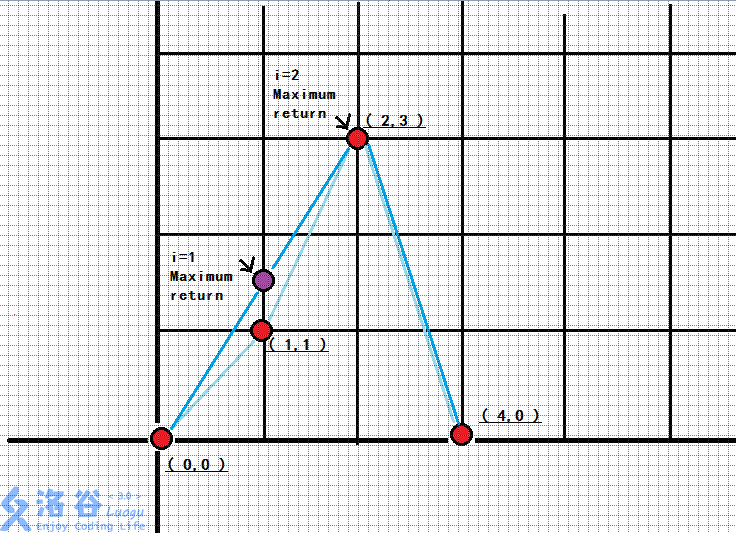
对于像 $f_i=\max(a_i,\frac{f_{i-1}+f_{i+1}}{2}-b_i)$ 这样的方程,考虑将 $b_i$ 配掉。
待定参数 $d_i$,令 $g_i=f_i+d_i,c_i=a_i+d_i$,得 $g_i=\max(c_i,\frac{g_{i-1}+g_{i+1}}{2}+d_i-b_i-\frac{d_{i-1}+d_{i+1}}{2})$。
只需令 $d_i-b_i-\frac{d_{i-1}+d_{i+1}}{2}=0$,方程就转化为了上述形式。
有向图的三染色:若对于每一个“弱连通块”(即只有),可以给所有顶点染3种颜色,使所有边均为 1->2,2->3 或 3->1,则称其为“三染色”。
注意:给有向图三染色时要记录每条有向边的反向边!
还有,注意特判弱连通块中只有两种颜色的情况!
【Codeforces Gym 101745E】Increasing Sequence
重要技巧:用线段树维护 $n$ 个矩阵的乘积,每次改变线段树中一个矩阵只需 $O(n \log n)$ 时间。
适用范围:求一个数 $k$ 对 $i=1,2,\dots,n-1$ 均满足 $i$ 到 $i+1$ 的某一种关系,可以将对关系的影响以及对应的 $k$ 的取值范围离线下来进行排序,然后用上面所说的线段树进行维护。
【AtCoder AGC041 F】Histogram Rooks
容斥的思想:要计算什么都有,就计算有 $i$ 个没有的方案数,然后进行容斥,即乘上系数 $(-1)^i$。
注意,用容斥进行 dp 的时候,要把容斥系数放在状态值里面,即若方案数为 $x$,最好令 $f[i]=(-1)^i x$。
容斥是可以套容斥的hhh
参考资料:https://blog.csdn.net/bzjr_Log_x/article/details/105410031 https://www.cnblogs.com/Itst/p/12612116.html
【CodeChef BOUNCE】Advanced Cooking Machine
大推式子+类欧几里得算法+杜教筛。
类欧几里得算法:求 $\sum\limits_{i=1}^n \frac{a*i+c}{b}$ 和 $\sum\limits_{i=1}^n i\frac{a*i+c}{b}$ 之类的式子。
技巧:把式子 $f(n,a,b,c)$ 用 $f(m,a \pmod b,b,c)$ 表示,复杂度就是 $O(\log n)$ 的。
杜教筛:积性函数 $O(n^{2/3})$ 求前缀和。
【CodeChef DIVISORS】Something About Divisors
归结起来就是求 $[1,n]$ 内“不是若干个数中任意一个数的倍数”的数的个数。(慢慢读
若干个数先去重,去倍数,过滤烘干
显然用容斥。只需要求出任意若干个数的 $\lcm$ 以及其系数即可。
按顺序递推,设 $S_i$ 为前 $i$ 个数的 $\lcm$ 的集合,则从 $S_i$ 向 $s_{i+1}$ 递推,可以排序去重合并系数。
注意本题数的值域很小 ($\leq 60$),于是预处理出所有质因子不超过 $60$ 的数,放在一个哈希表内以供取用。
排序省下了,合并系数也容易了。
注意本题卡常卡到人傻,列一些技巧:
- 预处理出所有 $\gcd$ 的值放到数组里面取用。
- 一个大数 $y$ 和一个小数的 $\lcm$ 记录小数 $x$ 的 $x/\gcd(x,i)$,然后用 $y*(x/\gcd(x,y \pmod x))$。
- 除法很费时间,乘法也很费时间,能少弄一次就少弄一次(什么话
- 哈希表千万不要取模,非常慢,用 $(x^(x<<3))&(H-1)$,其中 $H=2^k$。实测链表最大长度不大于 $10$。
- 预处理出所有质因子不超过 $60$ 的数,放在一个哈希表内以供取用,省去 vector 的麻烦。
- vector 很慢,要用就要 resize 完再用,一个一个 push_back 就T飞了。
- 多组询问离线下来,能一起弄的一起弄
- 离线下来之后,有什么信息要用就用掉,不要记录下来,记录很慢
- 不要拷贝数组,合并两个集合新的直接合并到旧的上去
- 火车头很好用🚂
面对“$n$ 个数中选 $k$ 个数”之类的问题,脑子里第一个想到指数型生成函数。
重要技巧:进行一个游戏,进行的期望次数=Σ(进行 i 次还没有停止的概率)。
证明:阿贝尔变换即可。
于是就可以设 $P(i)$ 为进行 $i$ 次的概率,令 $F(z)=\sum\limits_{i \geq 0} P(i)z^i$,则答案为 $F(z)$ 的系数和。
多项式乘法,得到 $F(z)=\sum\limits_{i=0}^{k-1} G(z)e^{i/k}$,其中 $G(z)$ 是关于 $z$ 的多项式。
可以 $O(n^3)$ 搞定。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号