How to die?
- 下次给一个 vector 搞 unique 之前,一定要记得给它排序!!1(少点自以为是)
- 对一个 set “同时”删除两个数时,一定要注意特判两个数是否重复/重叠。
- 有两个序列,一个长度为 $n$,一个长度为 $cnt$,给我看清楚 $cnt$ 有没有写成 $n$ (特别是草稿纸上推公式用的是 $n$ 的时候)
- 设置 dp 状态时,一定要分清一个状态代表什么,特别是一个状态 f[k] 当 k=n 时代表 k>=n 时的所有情况之类的。此时最好用顺推转移,避免漏掉情况。
- 大哥啊 Tarjan 有向图求强连通分量你记录 pa 干什么(
- Tarjan 缩点后建多条边后一定要注意你用的是哪个邻接数组,不然。。。0.5h
- 不要用 round(ceil(1.0*x/y)) 之类的东西,用这个:
 divceil()
divceil()int divceil(int x,int y) { if(x<=0) return x/y; else return (x-1)/y+1; } int divfloor(int x,int y) { return -divceil(-x,y); }
否则浮点误差很恐怖。。。
- n=2e7 千万别用 $O(n \log n)$ 的算法,即使是 $n=2 \times 10^3, m=1 \times 10^4, O(nm \log m)$ 也不行,会T,两行泪。。。
- 考试时一定一定要测空间,有一题做出来了63分,一看是爆空间,之前 NOI Online 有一题爆空间就0分,后怕。。
- 其实 #define int long long 对时间影响不大,最好开着(最短路时特别是判负环要注意爆 int)
- 写高精的时候要注意不能乱开大数组,空间*100,莫名挂分(
- 卡时:二维数组莫名耗时,改一维
- 分块 $bl[bnum[x]]$ 写成 $bl[x]$ 调 1h
- 一长行中 $y$ 写成 $x$ 调 1.5h
- Tarjan 求强连通分量 $ins$ 不清空调 20min
- $sort(pl1+1,pl1+1+c1,cmp1)$ 写成 $sort(pl1+1,pl1+c1,cmp1)$,调 45min
- 读入 char 要么用 cin>>ch; ,要么用 scanf(" %c",&ch); ,注意 %c 前面一定要有空格!
- ios::sync_with_stdio(false); + cout<<ans<<endl; + puts("-1"); = WA
- 傻瓜筛 $\mu$ 时质数赋值为 $-1$ 不是 $1$ -_-"
- 卡常:y=(x%mod+mod)%mod => y=x%mod; if(y<0) y+=mod
- 遇到数据输入 long long 类型的数时一定要小心,处处看着取模(这次是 inv(x) 中 x 没取模)
- 有向图 add(x,y): to[x].push_back(y); to[y].push_back(x); -_-"
- Tarjan 有向图求强连通分量弹栈 ins 不清掉,st[u]=++tp ahhhhh
- 永远慎用 continue/break,可能会跳过后面所需要的操作(
- Miller-Rabin 和 Pollar-Rho 很好用,但是一定要特判掉边界情况啊啊啊啊(我的 Pollar-Rho 在 n=4 时会炸掉💣)
- 求边双连通分量不要写 vector,用前向星 head&nxt&tot qwq
- 树链剖分求 lca 时,往上爬时,请比较 dep[top[x]] 和 dep[top[y]] 的大小(而不是 dep[x] 和 dep[y])
- $n$ 行 $m$ 列的网格图,判合法点:tx>=1 && tx<=n && ty>=1 && ty<=n (((
- AC 自动机中可以有自环,不要犯傻(
- AC 自动机求串不是 res[nxt[i]]+=res[i],而是将 nxt 指针建成一棵树,子树和为答案((((AC 自动机忘光了)
- new 出来的 struct 成员数组中的值并不会被初始化为 0,请慎重!!!
- 线段树维护序列 hash 值时,求区间 hash,设左右子树返回值为 v1, v2,则结果为 v1*pw[min(r,qr)-mid]+v2 而不是 v1*pw[qr-mid]+v2 !!!!!(花了近 1hr)
- 小心数据与描述不符!看这道题 https://loj.ac/p/154,“$S_i \neq S_j$ 当且仅当 $i \neq j$”,结果样例就有相同的。。。吃亏的还是你,浪费 1hr。。。
- 当你发现WA的时候,如果找一段时间没找出错,请及时判断是否存在数组越界,这种错,一定要留一根筋。。。
- 偷懒的后果:在询问 $2^{35}$ 级别的数中 1 的个数时使用了 __builtin_popcount(),应该使用 __builtin_popcountll()(安慰自己这不是在考场上,否则。。。
- 枚举集合不要用简单的 for,是 $O(2^nn)$ 的,仔细想想,$O(2^n)$ 的 dfs 不是好过。。。
- for(int i=0;i<40;i++) ans+=f(1<<i) = WA (•́へ•́╬)
- 有关线段树的题一定要小心是否存在 $n$ 为 0 或负数的情况,会 RE/TLE/MLE/WA,并且极难发现。尤其是当你要建大小为 $n-1$ 的线段树时要尤其注意!!1
- 分类讨论,嗯,不要闭着眼睛瞎调参,一个个仔细分析(废话),实在不行就对拍
- 当数组中要存负坐标的时候,一定一定要记得 +Z(特别是赋初值的时候)
- 使用概率生成函数求 $E(X),D(X)$ 时,一定要记住,结果是所有系数之和而不是所有系数*指数之和!!!
- 什么年代了还犯并查集不特判 fx==fy 的错误 (•́へ•́╬)
- 动态开点+合并的权值线段树上求前 k 大值之和,当递归到叶子节点时,一定不能返回叶子的所有 sum!(即 if(l==r) return sum[p] 是错的,if(l==r) return val[p]*x 才是对的!!!)
- 当手写 bitset 的时候(例如要记录 bitset 最低位时),一定要记住数组大小为 a[N/26+5] 而不是 a[N/26]!!!因为 N=1e5+5 时的 +5 已经被 /26 抵消掉了!!!
- 为什么到现在还会犯分段 dp 中 f[u][i] 写成 f[u][1] 的错。。。
- 被卡常时可以考虑预处理 $10^7$ 以内的乘法逆元(当你确信只会用到这些数的逆元的时候),复杂度 $O(n \log mod) \rightarrow O(n) $!
- 一道题要多次调用 Min_25 筛,用不同的函数,相同(或只差一个分母)的 $n$,一次就够了。。。会快无数。。。
- 在 USACO 赛场上敲差分约束用 Dijikstra 求最短路/fn/fn/fn
- 以后没开 $O(nm)$ 的复杂度就再也不写 SPFA 跑差分约束了,再也再也不写了

- $\frac14$ 并不是 $(mod-1)/4$,$\frac12$ 也不是 $(mod-1)/2$,是 $(mod+1)/2$!!!(学人家就要学清楚)
- 有时候,一个点的错误并不一定是因为边界情况没有判断,也可能是因为一些(中间的)地方没有考虑周全。。。牢记ARC134,花了半个小时找一个并不存在的边界问题,结果是被一组随机数据卡掉。。。
- 第一次尝试独立写 NTT:trinit() 中 (i&1?(n>>1):0) 写成 (i&1?(n<<1):0)

- 求平面凸包时一定要特判所有点在同一条直线上的情况
- 调试对拍的时候在另一个程序上改完没复制到被对拍的程序上去

- dfs 时回溯,即使不方便自己修改改动,也要让调用者来帮你改回来!!!
- 类欧几里得算法不需要特殊处理 $c<0$ 的情况,而是通过当 $a \ge b$ 或 $c \ge b$ 时均进行取模处理!
- (一次性问题)VSCode 上面手动开栈时 -Wl,--stack=268435456 前后需要加上 \" ,否则出错
- 枚举 Powerful Number 的时候绝对不是简简单单的 dfs,dfs 到 pcnt+1 就返回!!正确的方式:每 dfs 到一层就计算一次,dfs 的含义是保证此后还会乘上至少一个素因子,这样才能够保证枚举每个 PN 的复杂度是 $O(1)$(而不是 $O(pcnt)$)的!!!(还有注意这样会漏掉 1,要加回来)
- 永远永远记住,并不只是多测才需要清空!!!
- 不仅仅是 $n \ge 32$ 时 1<<n 会溢出,$n \ge 30$ 时 153*(1<<n) 也会溢出!!
- 让程序来帮助你做一部分的手玩样例来调试!人脑的力量是有限的!这才是程序的最终目的!帮你做事!
- 以后不要花上几个小时来卡常,看看人家是怎么写的,学一学!
- Dinic 求二分图最大匹配 N 只开到了点数大小没开到边数大小
- 写 Dinic dfs 时没有用流更新边权
- 倍增发一定要检查数组开的大小,一维数组很多要开到 N*21,并且注意是 21 而不是 20(习惯固定循环到20)(不会 RE 只会 WA,因为后面往往跟着一个很大的数组给你溢出用)
- “不妨设”等价交换 $x,y$ 的时候一定要记得同时交换记录下来的 $x,y$ 的所有信息!
- 请仔细想清楚你的程序时间复杂度,有时候很简单的一个均摊,你会发现自己想太多了
- 预处理阶乘、幂等数时,一定要多看几遍柿子,看清楚上界和下界,避免要用到的没预处理到!
- 不要疏忽 cin 与 cout 的“力量”,cout 5e3 行 endl 足以让你 TLE!!! 输入 5e3 个 5e3 的字符串也足以让你 TLE!!!
- 动态开点线段树请注意是否存在调用时 root=0 的情况,会在小数据而不是大数据出错,并不是 0 可以被函数忽略,它会造成莫名其妙的影响
- 平面几何:函数想计算 Point p[x] 却传入了 x 被自动转换了

- 平面几何:叉乘算三角形面积直接 /2 导致 1/2=0

- sort(lis+1,lis+1+n,[](int i,int j){return p[lis[i]].x<p[lis[j]].x;};
- FFT/FWT: for(int len=2;len<=(1<<n);len++)

- 动态开点线段树 pushdown 时请注意要新建两个儿子节点!!!
- 主席树新建节点,采取 newnode(x) 返回一份 x 的复制的方法处理,而不是像线段树合并那样 change 返回新建节点
- 做背包时,注意同层转移的情况,可能会重复转移出错(特别是物品大小为 0 时)
- 跑网络流时,特别是建模时,一定要注意你加了几个点几条边,好好数着,否则 RE 不说,WA 调半天/kk/fn
- 进行整体平移/翻转变换打标记时,有可能对于一些特殊部分单独处理了,这时候要着重看是否有重复标记这一部分!
- cin 一个 int,如果输入值大于 MAX_INT 的话将会产生不可预知的结果(所以即使你不使用这个读入的值也要小心!)



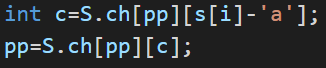



-
min-max 容斥时容斥系数应该是 $(-1)^{|S|-1}$(而不是 $(-1)^{|S|}$)
- 矩形离散化时不要把询问矩形一起离散下来啊。。只离散原来的点就可以了。。
- FWT(FFT)时写了 for(int o=2;o<=n;o++) 而不是 int w=1; while(w<=n) w<<=1; for(int o=2;o<=w;o<<=1)
- 请多次检查是否该开 long long 的地方都开了 long long
- 李超树一定要小心 $[l,r]$ 是 $[-1e9,1e9]$ (溢出)还是 $[-1e5,1e5]$ 还是 $[1,1e5]$ 还是 $[0,1e5]$ !!!
- FFT 封装后一定要严格传入函数的次数,否则 FFT 可能用到未知的数
- 用记忆化搜索代替返回一段区间的结果
- 莫队进行区间移动时,其它区间一定要对莫队的左右端点(而不是其左右端点)取 min/max!!!!!!
- multiset::count() 的时间复杂度是 $O(c)$ 的,其中 $c$ 是 multiset 中所查询元素的个数!!!所以查询是否存在请用 st.find()!=st.end() !!!
- 永记 JOI2022 的教训:做题时看清楚**所有**数据范围!!!包括边权,值域之类的“次要”的数据范围!!!
- 线段树节点维护整个区间前缀和 min 之类的信息时,请注意递归时要加上左边的 delta!
- Matrix-Tree 定理中重边没有进行重复加边权!!!
- 当你的数组大小包含 N*N 时,一定要重复检查是否有漏写成 N 的!!!
- 当忽略很小的浮点数时,一定要最后再忽略,否则误差会滚雪球,造成大错!
- 吉司机线段树中一定要看更新的数能不能更!不是随便往上赋值完事!
- 对于 dp 方程,尽管答案在 long long 范围内,也有可能有爆 long long 的数参与 min 运算!!!一定一定要特判!!!
- 点分治时对于全局变量的改变一定要注意/ll
- 欧拉序列除了 mn 数组开两倍,lg2 数组也要开两倍!!
-
for(int v:son[u]){ Rev(i,t+siz[v],0){ tmp[i]=1ll*tmp[i]*f[v][0]%mod; int lim=min(i,siz[v]); For(j,1,lim){ tmp[i]=(tmp[i]+1ll*tmp[i-j]*f[v][j])%mod; } } t+=siz[v]; }这个复杂度是错的,因为当 j 较小时 tmp[i-j] 就没用了。。。
- 后缀树 LCA 计算 lcp 长度时,长度是 SAM 中求出的 len 而不是树中的 dep!
- 单调队列优化多重背包要先插入后取值!!!
-
void set(int x,ull o) { a[x>>6]|=o<<(x&63); }/ll
-
并查集不要爸了555555
- FWT:for(int i=2;i<(1<<n);i++)/fn/fn/fn/fn/fn/fn/fn
- 用 set 来维护前缀/后缀最小值时,一定要小心是否相同位置存在多个数!可能会出错!
- 代码中注意统一 INF 的值!0x3f3f3f3f>1e9 判无穷时会出现问题!




