20130623-大地四边形的计算
1、界面
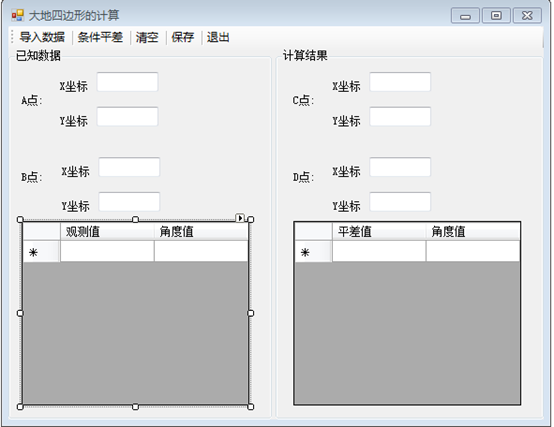
1.1界面结构

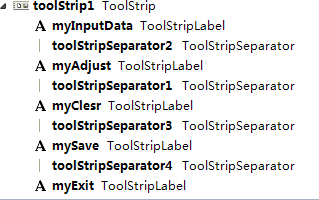
2解决方案
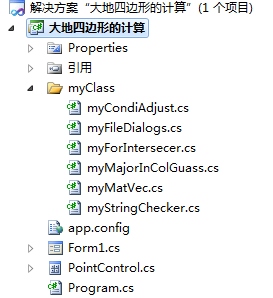
3类设计
3.1条件平差的类
/// <summary>
/// Abstract:
///条件平差
/// </summary>
class myCondiAdjust
{
/*--------------------------------------class comment
Version : V1.0
Coded by : 郑承良
Date : 2013/6/20 19:03:51
CLR Version : 4.0.30319.296
----------------------------------------------------
Desciption :
*
parameters :
*
Methods :
*
--------------------------------------------------*/
public static void CondiAdjust( MAT B, MAT P, VEC W,out VEC V)
{
Int32 b1, b2, p1, p2;
b1 = B.dim1;
b2 = B.dim2;
p1 = P.dim1;
p2 = P.dim2;
MAT Bt = new MAT(b2,b1);
MAT QBt = new MAT(b2,b1);
MAT Nbb = new MAT(b1,b1);
VEC K=new VEC(b1);
MAT Q = new MAT(p1, p2);
for (Int32 i = 0; i < p1; i++)
{
Q.ele[i, i] = 1 / P.ele[i, i];
}
Bt = ~B;
QBt = Q | Bt;
Nbb = B | QBt;
//列选主元
//myMajorInColGuass.MajorInColGuass(Nbb, W, K);
myMajorInColGuass myM = new myMajorInColGuass();
myM.MajorInColGuass(Nbb, W,out K);
V = QBt | K;
}
}
3.2对话框
class myFileDialogs
{
/*--------------------------------------class comment
Version : V1.0
Coded by : 郑承良
Date : 2013/6/19 22:07:08
CLR Version : 4.0.30319.296
----------------------------------------------------
Desciption :
* 打开与保存对话框
parameters :
*
Methods :
*
--------------------------------------------------*/
public static String myOpenFile()
{
string myReturn;
OpenFileDialog myOpenFile = new OpenFileDialog();
myOpenFile.Filter = "数据源.txt|*txt";
myOpenFile.CheckPathExists = true;
myOpenFile.ShowDialog();
//DialogResult myResult = new DialogResult();
//if (myOpenFile.FileName != String.Empty)
if (File.Exists(myOpenFile.FileName))
{
myReturn = myOpenFile.FileName;
//myFile = null;
myOpenFile.Dispose();
return myReturn;
}
else
{
return null;
}
}
public static String mySaveFile()
{
string myReturn = "";
SaveFileDialog myFile = new SaveFileDialog();
//myFile.Title = myStyle;
myFile.Filter = "文本文档|*txt";
myFile.ShowDialog();
//DialogResult myResult = new DialogResult();
if (myFile.FileName != String.Empty)
{
myReturn = myFile.FileName;
//myFile = null;
myFile.Dispose();
return myReturn;
}
else
{
return myReturn;
}
}
}
3.3前方交回

/// <summary>
/// Abstract :
///前方交会
/// </summary>
using System;
class myForIntersecer
{
/*--------------------------------------class comment
Version : V1.0
Coded by : 郑承良
Date : 2013/6/20 18:57:31
CLR Version : 4.0.30319.296
----------------------------------------------------
parameters :
*
Methods :
*
--------------------------------------------------*/
public static double DegreeToRadian(double ang)
{
int fuhao = (int)(ang / Math.Abs(ang));
ang = Math.Abs(ang);
int du = (int)ang;
int fen = ((int)(ang * 100)) - du * 100;
double miao = ang * 10000 - fen * 100 - du * 10000;
Double myReturn = ((du + fen / 60.0 + miao / 3600.0) * fuhao) / 180.0 * Math.PI;
//myReturn = myReturn.ToString("F2");
return myReturn;
}
public static String RadianToDegree(Double ang)
{
string myReturn;
ang = ang * 180 / Math.PI;
int du=(int)ang;
int fen = (int)((ang-du)*60+0.5);
int miao =(int)((ang - du - fen / 60) * 3600);
myReturn = du.ToString() + "." + fen.ToString() + miao.ToString();
myReturn = Convert.ToDouble(myReturn).ToString("F4");
return myReturn;
}
internal static void ForIntersec(Double Xa, Double Ya, Double Xb, Double Yb, Double a, Double b, out Double Xp, out Double Yp)
{
Double ctga, ctgb;
ctga = 1 / Math.Tan(DegreeToRadian(a));
ctgb = 1 / Math.Tan(DegreeToRadian(b));
Xp = (Xa * ctgb + Xb * ctga + (Yb - Ya)) / (ctga + ctgb);
Yp = (Ya * ctgb + Yb * ctga + (Xa - Xb)) / (ctga + ctgb);
}
}
3.4列选主元
/// <summary>
/// Abstract :
///列选主元消去法
/// </summary>
class myMajorInColGuass
{
/*--------------------------------------class comment
Version : V1.0
Coded by : syz
Date : 2011-06-20 11:26:45 *星期一*
Version : V1.0
Coded by : 郑承良(使用)
Date : 2013/6/20 20:34:16
CLR Version : 4.0.30319.296
----------------------------------------------------
Desciption :
*
parameters :
*
Methods :
*
--------------------------------------------------*/
public void MajorInColGuass(MAT A, VEC b, out VEC x)
{
/*------------------------------------------ comment
Author : syz
Date : 2011-06-20 10:59:59
---------------------------------------------------
Desciption :
* 消去法解线性方程组
Post Script :
* 要用到上三角方程的回代方法
paramtegers :
* A---方程组系数矩阵
* b---右向量
* x---计算结果
*
-------------------------------------------------*/
int n, i, j, k;
n = b.dim;
//方程维数
double tmp;
//增广矩阵
MAT Ab = new MAT(n, n + 1);
//赋值给增广矩阵
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
Ab.ele[i, j] = A.ele[i, j];
Ab.ele[i, n] = b.ele[i];
}
double elmax;
int id_max;
double tmp1, tmp2;
//这段是高斯消去法的核心
for (k = 0; k <= n - 2; k++)
{
//主元素初值
elmax = Math.Abs(Ab.ele[k, k]);
//主元素标号
id_max = k;
//下面一段为找出主元素所在的行
//即获得主元素标号的值
for (i = k + 1; i <= n - 1; i++)
{
if (Math.Abs(Ab.ele[i, k]) > elmax)
{
elmax = Math.Abs(Ab.ele[i, k]);
//注意这里把该元素的绝对值复制给最大元素
//不能把该元素本身复制给最大元素
id_max = i;
}
}
//至此已经完成查找最大元素所在行标号
//下面交换两行元素,其他量不变
//n+1个元素,该循环为交换两行元素
for (i = 0; i < n + 1; i++)
{
tmp1 = Ab.ele[k, i];
tmp2 = Ab.ele[id_max, i];
Ab.ele[k, i] = tmp2;
Ab.ele[id_max, i] = tmp1;
}
//交换后实施消去
for (i = k + 1; i <= n - 1; i++)
{
tmp = Ab.ele[i, k] / Ab.ele[k, k];
for (j = 0; j < n + 1; j++)
Ab.ele[i, j] = Ab.ele[i, j] - tmp * Ab.ele[k, j];
}
}
//在C#中使用传值方法,不会改变原始变量的值
//而在Fortran中是使用传地址,如果这样的话,会改变输入变量的外部值
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
A.ele[i, j] = Ab.ele[i, j];
b.ele[i] = Ab.ele[i, n];
}
uptri(A, b, out x);
}
public void uptri(MAT A, VEC b, out VEC x)
{
/*------------------------------------------ comment
Author : syz
Date : 2011-06-17 10:04:27
---------------------------------------------------
Desciption :
* 上三角矩阵方程解法
Post Script :
* 要用到MAT 与 VEC 类
paramtegers :
* A-----系数矩阵
* b-----右向量
* x-----方程的解
-------------------------------------------------*/
int N;
N = A.dim1;
//获取方程维数
x = new VEC(N);
x.ele[N - 1] = b.ele[N - 1] / A.ele[N - 1, N - 1];
for (int i = N - 2; i >= 0; i--)
{
x.ele[i] = b.ele[i];
for (int j = i + 1; j <= N - 1; j++)
x.ele[i] = x.ele[i] - A.ele[i, j] * x.ele[j];
x.ele[i] = x.ele[i] / A.ele[i, i];
}
}
}
3.5矩阵与向量类


class MAT
{
/*--------------------------------------class comment
Version : V1.0
Coded by : syz
Date : 2011-06-16 16:53:40 *星期四*
----------------------------------------------------
Desciption :
* 矩阵类
* 该类中的部分算符重载需要用到VEC类
parameters :
*
Methods :
* MAT------构造函数
* + --------两矩阵相加(对应元素分别相加)
* - --------矩阵相减(对应元素分别相减)
* * --------矩阵元素分别相乘(相当于MATLAB中的 .*算符)
* / --------矩阵元素分别相除(相当与MATLAB中的 ./算符)
*
* + --------矩阵加实数(所有元素分别加该实数)
* - --------矩阵减实数(所有元素分别减该实数)
* * --------矩阵乘实数(所有元素分别乘该实数)
* / --------矩阵除实数(所有元素分别除该实数)
*
* 以下再次重载四则算符,
* 如此可以在矩阵左右均可进行与实数的双目运算
* + --------实数加矩阵(所有元素分别加该实数)
* - --------实数减矩阵(所有元素分别减该实数)
* * --------实数乘矩阵(所有元素分别乘该实数)
* / --------<无>---不重载--(即不能用实数除以矩阵)
*
* | --------数学意义下的矩阵相乘
* | --------矩阵与向量相乘(线性变换)
* ~ --------矩阵转置(向量中~该算符用于求2范数平方)
--------------------------------------------------*/
public int dim1, dim2; //数组维数
public double[,] ele;
public MAT(int m, int n)
{
//构造函数
dim1 = m;
dim2 = n;
//矩阵维数
ele = new double[m, n];
//用二维数组构造数学意义下的矩阵
//矩阵元素保存于对象ele中
}
//-------两个矩阵加法算符重载
//------矩阵元素分别相加
public static MAT operator +(MAT a1, MAT a2)
{
int m, n;
m = a1.dim1;
n = a1.dim2;
MAT a3 = new MAT(m, n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
a3.ele[i, j] = a1.ele[i, j] + a2.ele[i, j];
return a3;
}
//-------两个矩阵减法算符重载
//------矩阵元素分别相减
public static MAT operator -(MAT a1, MAT a2)
{
int m, n;
m = a1.dim1;
n = a1.dim2;
MAT a3 = new MAT(m, n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
a3.ele[i, j] = a1.ele[i, j] - a2.ele[i, j];
return a3;
}
//-------两个矩阵乘法算符重载
//------矩阵元素分别相乘,相当于MATLAB中的 .*
// 要求两个矩阵维数相同,矩阵类不进行个数判断
public static MAT operator *(MAT a1, MAT a2)
{
int m, n;
m = a1.dim1;
n = a1.dim2;
MAT a3 = new MAT(m, n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
a3.ele[i, j] = a1.ele[i, j] * a2.ele[i, j];
return a3;
}
//-------两个矩阵除法算符重载
//------矩阵元素分别相除,相当于MATLAB中的 ./
// 要求两个矩阵维数相同,矩阵类不进行个数判断
public static MAT operator /(MAT a1, MAT a2)
{
int m, n;
m = a1.dim1;
n = a1.dim2;
MAT a3 = new MAT(m, n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
a3.ele[i, j] = a1.ele[i, j] / a2.ele[i, j];
return a3;
}
//矩阵加实数算符重载
//各分量分别加实数
public static MAT operator +(MAT a1, double x)
{
int m, n;
m = a1.dim1;
n = a1.dim2;
MAT a2 = new MAT(m, n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
a2.ele[i, j] = a1.ele[i, j] + x;
return a2;
}
//矩阵减实数算符重载
//各分量分别减实数
public static MAT operator -(MAT a1, double x)
{
int m, n;
m = a1.dim1;
n = a1.dim2;
MAT a2 = new MAT(m, n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
a2.ele[i, j] = a1.ele[i, j] - x;
return a2;
}
//矩阵乘以实数算符重载
//各分量分别乘以实数
public static MAT operator *(MAT a1, double x)
{
int m, n;
m = a1.dim1;
n = a1.dim2;
MAT a2 = new MAT(m, n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
a2.ele[i, j] = a1.ele[i, j] * x;
return a2;
}
//矩阵除以实数算符重载
//各分量分别除以实数
public static MAT operator /(MAT a1, double x)
{
int m, n;
m = a1.dim1;
n = a1.dim2;
MAT a2 = new MAT(m, n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
a2.ele[i, j] = a1.ele[i, j] / x;
return a2;
}
//实数加矩阵算符重载
//各分量分别加实数
public static MAT operator +(double x, MAT a1)
{
int m, n;
m = a1.dim1;
n = a1.dim2;
MAT a2 = new MAT(m, n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
a2.ele[i, j] = a1.ele[i, j] + x;
return a2;
}
//实数减矩阵算符重载
//各分量分别减实数
public static MAT operator -(double x, MAT a1)
{
int m, n;
m = a1.dim1;
n = a1.dim2;
MAT a2 = new MAT(m, n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
a2.ele[i, j] = a1.ele[i, j] - x;
return a2;
}
//实数乘矩阵算符重载
//各分量分别乘以实数
public static MAT operator *(double x, MAT a1)
{
int m, n;
m = a1.dim1;
n = a1.dim2;
MAT a2 = new MAT(m, n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
a2.ele[i, j] = a1.ele[i, j] * x;
return a2;
}
//数学上的矩阵相乘
public static MAT operator |(MAT a1, MAT a2)
{
int m, n, p, q;
m = a1.dim1;
n = a1.dim2;
p = a2.dim1;
q = a2.dim2;
if (n != p) System.Console.WriteLine("Inner matrix dimensions must agree!");
//如果矩阵维数不匹配给出告警信息
//新矩阵,用于存放结果
MAT a3 = new MAT(m, q);
int i, j;
for (i = 0; i < m; i++)
for (j = 0; j < q; j++)
{
a3.ele[i, j] = 0.0;
for (int k = 0; k < n; k++)
a3.ele[i, j] = a3.ele[i, j] + a1.ele[i, k] * a2.ele[k, j];
}
return a3;
}
//矩阵乘以向量(线性变换)
//即 b=Ax
public static VEC operator |(MAT A, VEC x)
{
int m, n, p;
m = A.dim1;
n = A.dim2;
p = x.dim;
if (n != p) System.Console.WriteLine("Inner matrix dimensions must agree!");
//如果矩阵维数不匹配,给出告警信息
VEC b = new VEC(m);
for (int i = 0; i < m; i++)
{
b.ele[i] = 0.0;
for (int k = 0; k < n; k++)
b.ele[i] = b.ele[i] + A.ele[i, k] * x.ele[k];
}
return b;
}
//矩阵转置
public static MAT operator ~(MAT A)
{
int m, n;
m = A.dim1;
n = A.dim2;
MAT TA = new MAT(n, m);
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
TA.ele[i, j] = A.ele[j, i];
return TA;
}
public double this[int index1, int index2]
// 矩阵索引器
{
get
{
return ele[index1, index2];
}
set
{
ele[index1, index2] = value;
}
}
}
class VEC
/*--------------------------------------class comment
Version : V1.0
Coded by : syz
Date : 2011-06-15 12:50:11 *星期三*
----------------------------------------------------
Desciption :
向量类
parameters :
* dim------向量维数
* ele------向量元素
*
Methods :
* = -----------向量相等
* 注意该方法不需要自行编写重载函数,
* c#已经实现了对类的等号算符重载,并禁止
* 用户编写等号算符(=)重载函数
* + -----------两向量对应元素相加
* - -----------两向量对应元素相减
* * -----------两向量对应元素相乘(相当于MATLAB中的 .*算符)
* / -----------两向量对应元素相除(相当于MATLAB中的 ./算符)
*
* + -----------重载向量加一实数(所有元素)
* - -----------重载向量减一实数(所有元素)
* * -----------重载向量乘一实数(所有元素)
* / -----------重载向量除一实数(所有元素)
*
* + -----------重载实数加向量(所有元素)
* - -----------重载实数减向量(所有元素)
* * -----------重载实数乘以向量(所有元素)
* / -----------<无>--不重载--<即不能用实数除以向量>
*
* | (VEC1|ve2)----向量内积
* ~ (~VEC1)-------向量2范数的平方
* - (-VEC1)-------向量取负
* ^ (VEC1^VEC2)---向量外积
*
--------------------------------------------------*/
{
public int dim; //数组维数
public double[] ele;
public VEC(int m)
{
//构造函数
dim = m;
ele = new double[dim];
//用一维数组构造向量
}
//-------两个向量加法算符重载
//------分量分别相加
public static VEC operator +(VEC v1, VEC v2)
{
int N0;
//获取变量维数
N0 = v1.dim;
VEC v3 = new VEC(N0);
int j;
for (j = 0; j < N0; j++)
{
v3.ele[j] = v1.ele[j] + v2.ele[j];
}
return v3;
}
//-----------------向量减法算符重载
//-----------------分量分别想减
public static VEC operator -(VEC v1, VEC v2)
{
int N0;
//获取变量维数
N0 = v1.dim;
VEC v3 = new VEC(N0);
int j;
for (j = 0; j < N0; j++)
{
v3.ele[j] = v1.ele[j] - v2.ele[j];
}
return v3;
}
//----------------向量乘法算符重载
//-------分量分别相乘,相当于MATLAB中的 .*算符
public static VEC operator *(VEC v1, VEC v2)
{
int N0;
//获取变量维数
N0 = v1.dim;
VEC v3 = new VEC(N0);
int j;
for (j = 0; j < N0; j++)
{
v3.ele[j] = v1.ele[j] * v2.ele[j];
}
return v3;
}
//---------------向量除法算符重载
//--------------分量分别相除,相当于MATLAB中的 ./算符
public static VEC operator /(VEC v1, VEC v2)
{
int N0;
//获取变量维数
N0 = v1.dim;
VEC v3 = new VEC(N0);
int j;
for (j = 0; j < N0; j++)
{
v3.ele[j] = v1.ele[j] / v2.ele[j];
}
return v3;
}
//向量减加实数
//各分量分别加实数
public static VEC operator +(VEC v1, double a)
{
//向量数加算符重载
int N0;
//获取变量维数
N0 = v1.dim;
VEC v2 = new VEC(N0);
int j;
for (j = 0; j < N0; j++)
{
v2.ele[j] = v1.ele[j] + a;
}
return v2;
}
//向量减实数
//各分量分别减实数
public static VEC operator -(VEC v1, double a)
{
//向量数加算符重载
int N0;
//获取变量维数
N0 = v1.dim;
VEC v2 = new VEC(N0);
int j;
for (j = 0; j < N0; j++)
{
v2.ele[j] = v1.ele[j] - a;
}
return v2;
}
//向量数乘
//各分量分别乘以实数
public static VEC operator *(VEC v1, double a)
{
int N0;
//获取变量维数
N0 = v1.dim;
VEC v2 = new VEC(N0);
int j;
for (j = 0; j < N0; j++)
{
v2.ele[j] = v1.ele[j] * a;
}
return v2;
}
//向量数除
//各分量分别除以实数
public static VEC operator /(VEC v1, double a)
{
int N0;
//获取变量维数
N0 = v1.dim;
VEC v2 = new VEC(N0);
int j;
for (j = 0; j < N0; j++)
{
v2.ele[j] = v1.ele[j] / a;
}
return v2;
}
//实数加向量
public static VEC operator +(double a, VEC v1)
{
//向量数加算符重载
int N0;
//获取变量维数
N0 = v1.dim;
VEC v2 = new VEC(N0);
int j;
for (j = 0; j < N0; j++)
{
v2.ele[j] = v1.ele[j] + a;
}
return v2;
}
//实数减向量
public static VEC operator -(double a, VEC v1)
{
//向量数加算符重载
int N0;
//获取变量维数
N0 = v1.dim;
VEC v2 = new VEC(N0);
int j;
for (j = 0; j < N0; j++)
{
v2.ele[j] = v1.ele[j] - a;
}
return v2;
}
//向量数乘
public static VEC operator *(double a, VEC v1)
{
int N0;
//获取变量维数
N0 = v1.dim;
VEC v2 = new VEC(N0);
int j;
for (j = 0; j < N0; j++)
{
v2.ele[j] = v1.ele[j] * a;
}
return v2;
}
//---------------向量内积
public static double operator |(VEC v1, VEC v2)
{
int N0, M0;
//获取变量维数
N0 = v1.dim;
M0 = v2.dim;
if (N0 != M0)
System.Console.WriteLine("Inner vector dimensions must agree!");
//如果向量维数不匹配,给出告警信息
double sum;
sum = 0.0;
int j;
for (j = 0; j < N0; j++)
{
sum = sum + v1.ele[j] * v2.ele[j];
}
return sum;
}
//-----------向量外积(相当于列向量,乘以横向量)
public static MAT operator ^(VEC v1, VEC v2)
{
int N0, M0;
//获取变量维数
N0 = v1.dim;
M0 = v2.dim;
if (N0 != M0)
System.Console.WriteLine("Inner vector dimensions must agree!");
//如果向量维数不匹配,给出告警信息
MAT vvmat = new MAT(N0, N0);
for (int i = 0; i < N0; i++)
for (int j = 0; j < N0; j++)
vvmat[i, j] = v1[i] * v2[j];
//返回外积矩阵
return vvmat;
}
//---------------向量模的平方
public static double operator ~(VEC v1)
{
int N0;
//获取变量维数
N0 = v1.dim;
double sum;
sum = 0.0;
int j;
for (j = 0; j < N0; j++)
{
sum = sum + v1.ele[j] * v1.ele[j];
}
return sum;
}
// 负向量
public static VEC operator -(VEC v1)
{
int N0 = v1.dim;
VEC v2 = new VEC(N0);
for (int i = 0; i < N0; i++)
v2.ele[i] = -v1.ele[i];
return v2;
}
public double this[int index]
/*------------------------------------------ comment
Author : syz
Date : 2011-07-03 19:53:28
---------------------------------------------------
Desciption : 创建索引器
*
Post Script :
*
paramtegers :
*
-------------------------------------------------*/
{
get
{
//get accessor
return ele[index];
}
set
{
//set accessor
ele[index] = value;
}
}
}
3.6判断字符串是否是数字的类

/// <summary>
/// Abstract :
///判断是否是数字
/// </summary>
class myStringChecker
{
/*--------------------------------------class comment
Version : V1.0
Coded by : 郑承良
Date : 2013/6/20 22:15:32
CLR Version : 4.0.30319.296
----------------------------------------------------
Desciption :
* 此方法来源于网络
parameters :
*
Methods :
*
--------------------------------------------------*/
/// <summary>
///判断是否是数字
/// </summary>
/// <param name="strNumber"></param>
/// <returns></returns>
public static bool IsNumber(string strNumber)
{
Regex objNotNumberPattern = new Regex("[^0-9.-]");
Regex objTwoDotPattern = new Regex("[0-9]*[.][0-9]*[.][0-9]*");
Regex objTwoMinusPattern = new Regex("[0-9]*[-][0-9]*[-][0-9]*");
String strValidRealPattern = "^([-]|[.]|[-.]|[0-9])[0-9]*[.]*[0-9]+$";
String strValidIntegerPattern = "^([-]|[0-9])[0-9]*$";
Regex objNumberPattern = new Regex("(" + strValidRealPattern + ")|(" + strValidIntegerPattern + ")");
return !objNotNumberPattern.IsMatch(strNumber) &&
!objTwoDotPattern.IsMatch(strNumber) &&
!objTwoMinusPattern.IsMatch(strNumber) &&
objNumberPattern.IsMatch(strNumber);
}
}
3.7PointControl类
3.7.1控件界面:
3.7.2控件代码:
public partial class PointControl : UserControl
{
private String x, y;
public PointControl()
{
InitializeComponent();
x = "";
y = "";
}
public String X
{
get
{
return x;
}
set
{
if (myClass.myStringChecker.IsNumber(value) || value.Equals(String.Empty))
{
x = value;
this.textBox1.Text = value;
}
}
}
public string Y
{
get
{
return y;
}
set
{
if (myClass.myStringChecker.IsNumber(value)||value.Equals(String.Empty))
{
y = value;
this.textBox2.Text = value;
}
}
}
private void textBox1_TextChanged(object sender, EventArgs e)
{
InPut(textBox1,ref x);
}
private void textBox2_TextChanged(object sender, EventArgs e)
{
InPut(textBox2,ref y);
}
//当第一次输入非数字字符时,会小bug,即"请输入数字"会提示两遍
private void InPut(TextBox myBox,ref string eStr)
{
if (myClass.myStringChecker.IsNumber(myBox.Text))
{
eStr = myBox.Text;
}
else
{
// MessageBox.Show("请输入数字");
myBox.Text =eStr;
}
}
//private void textBox1_TextChanged(object sender, EventArgs e)
//{
// textBox1.DataBindings.Add("Text", this, "x");
// textBox2.DataBindings.Add("Text", this, "y");
//}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号