李宏毅机器学习组队学习打卡活动day04---深度学习介绍和反向传播机制
写在前面
报了一个组队学习的活动，今天的任务是深度学习，深度学习之前没有怎么接触，这次可以好好学习一下。
参考视频:https://www.bilibili.com/video/av59538266
参考笔记：https://github.com/datawhalechina/leeml-notes
深度学习介绍
深度学习的三个步骤
deep learning 一般有三个部分：
- step1:神经网络(Neural network)
- step2: 模型评估(Goodness of function)
- step3: 选择最优函数(Pick best function)
step1:神经网络
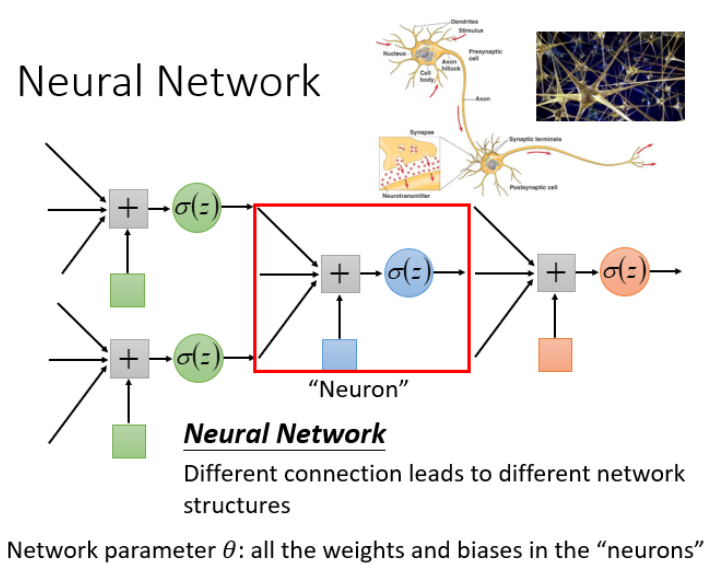
神经元：神经网络里面的节点
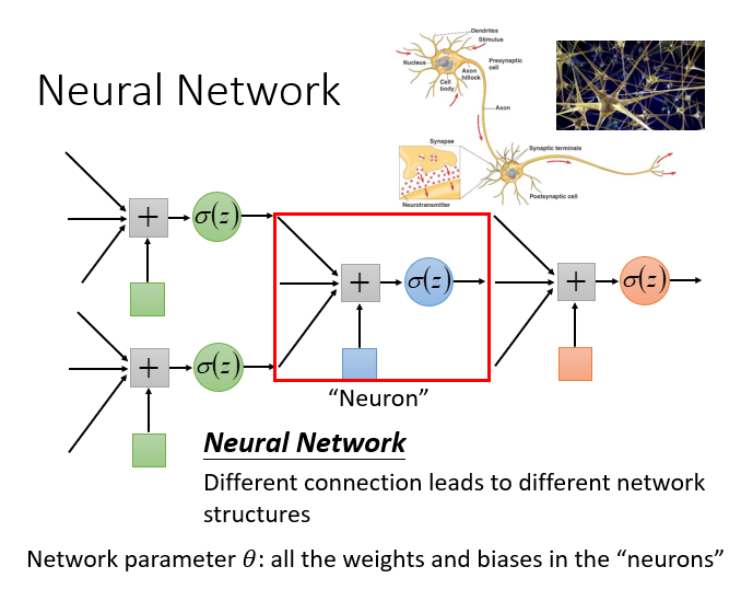
神经网络有很多不同的连接方式，这样会产生不同的结构。
完全前馈神经网络
概念：前馈(feedforward)也可以称为前向，从信号流向来理解就是输入信号进入网络后，信号流动是单项的，即信号从前一层流向后一层，一直到输出层，其中任意两层之间的连接并没有反馈(feedback)，亦即信号没有从后一层又返回到前一层。
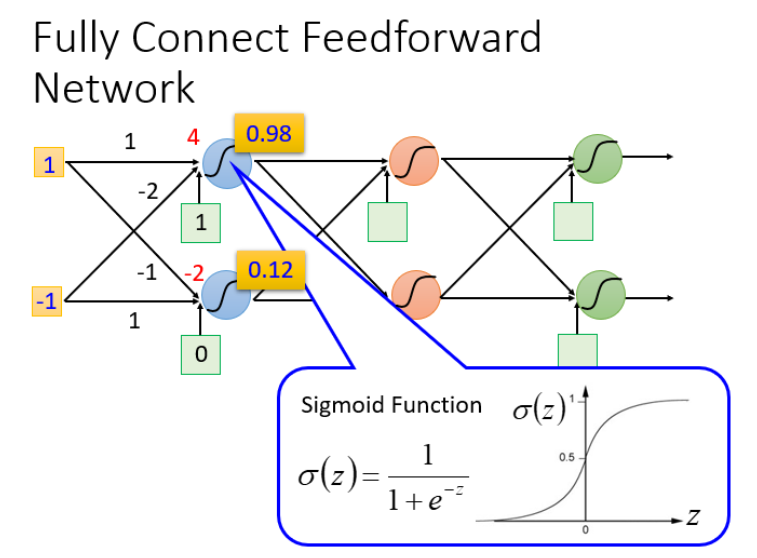
例如输入(1，-1)和(-1,0)的结果：
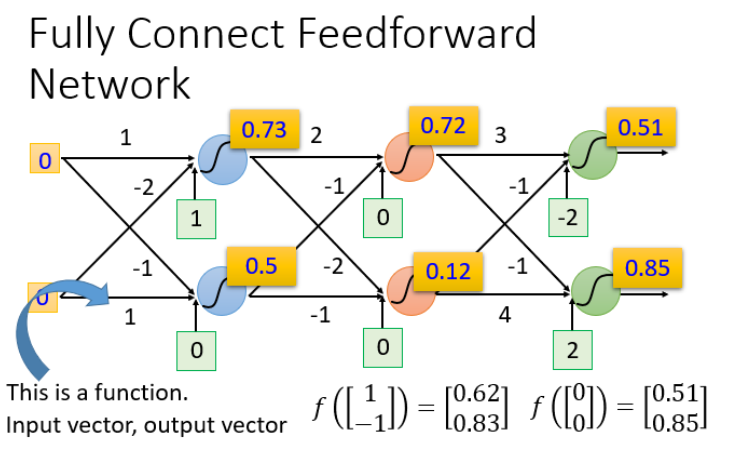
我们可以给上面的结构的参数设置为不同的数，就是不同的函数（function）。这些可能的函数（function）结合起来就是一个函数集（function set）。
全链接和前馈的理解
- 输入层（Input Layer）：1层
- 隐藏层（Hidden Layer）：N层
- 输出层（Output Layer）：1层
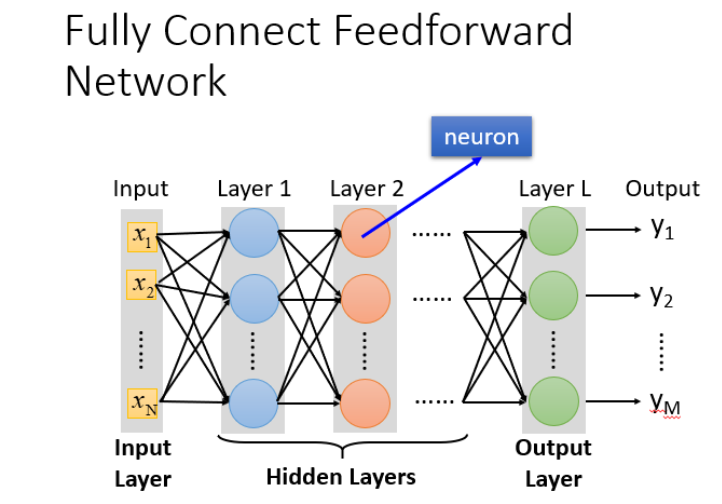
全连接的理解: 因为layer与layer2之间凉凉都有连接，所以叫做全链接(Fully Connect)
前馈的理解: 因为传递的方向是由后往前传，所以叫做Feedforward.
深度的理解
那什么叫做Deep呢？Deep = Many hidden layer。那到底可以有几层呢？
随着层数变多，错误率降低，随之运算量增大，通常都是超过亿万级的计算。采用矩阵运算可以加快运算速度。
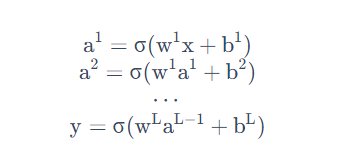
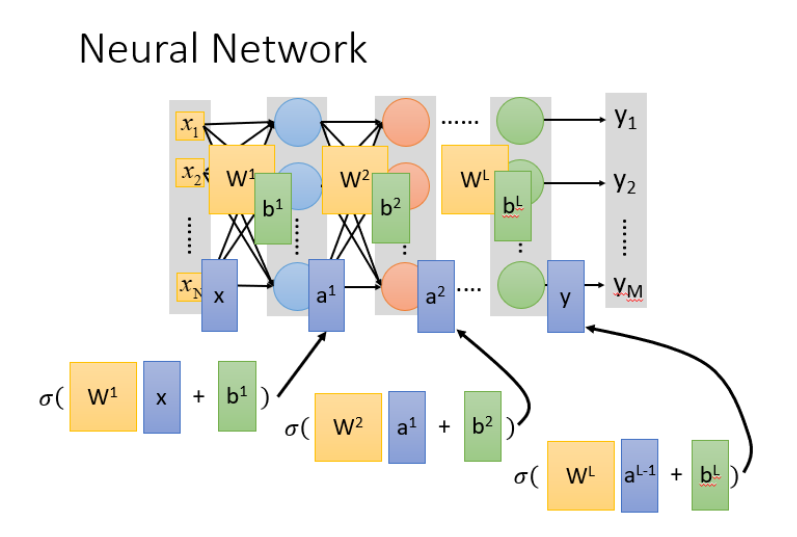
本质：通过隐藏层进行特征转换
把隐藏层通过特征提取来替代原来的特征工程，这样在最后一个隐藏层输出的就是一组新的特征（相当于黑箱操作）而对于输出层，其实是把前面的隐藏层的输出当做输入（经过特征提取得到的一组最好的特征）然后通过一个多分类器（可以是softmax函数）得到最后的输出y。
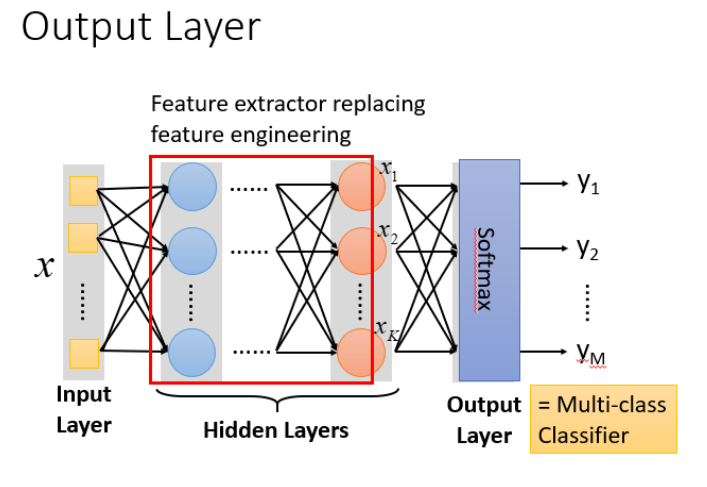
step2:模型评估
损失示例：
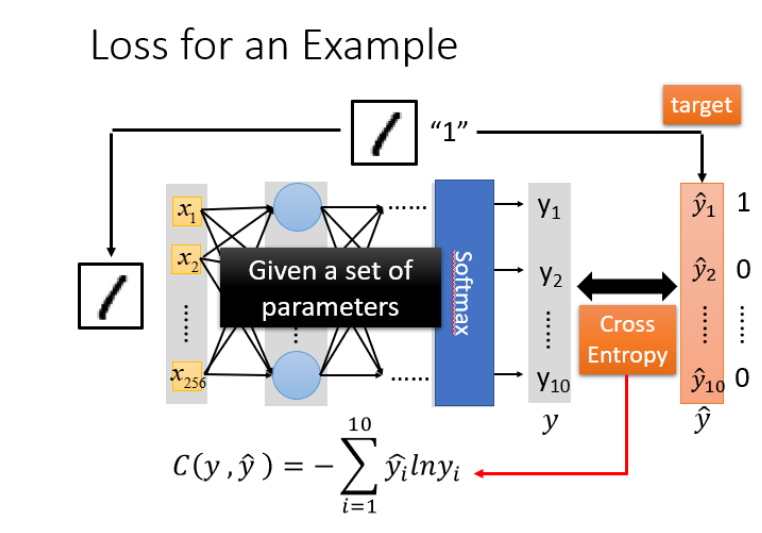
对于损失，我们不单单要计算一笔数据的，而是要计算整体所有训练数据的损失，然后把所有的训练数据的损失都加起来，得到一个总体损失L。
对于模型的评估。我们一般采用损失函数来反映模型的好坏，对于神经网络，一般采用交叉熵(cross entropy)函数进行计算。
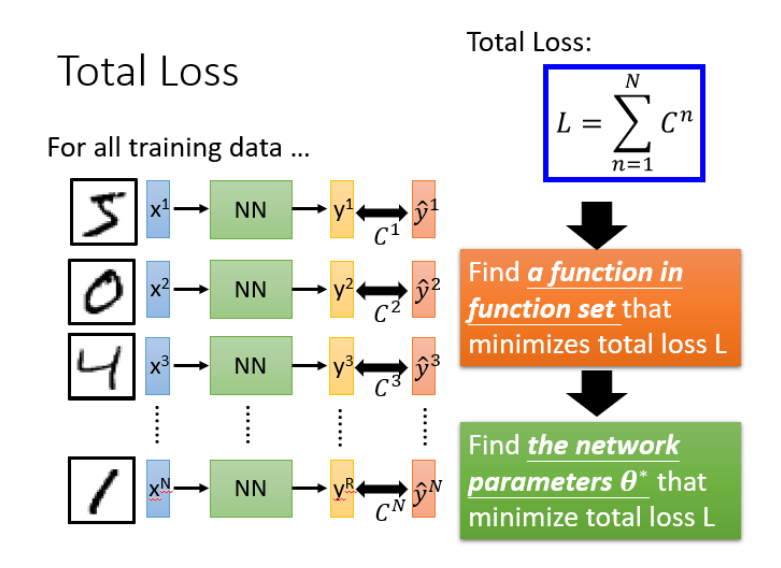
step3:选择最优函数
梯度下降
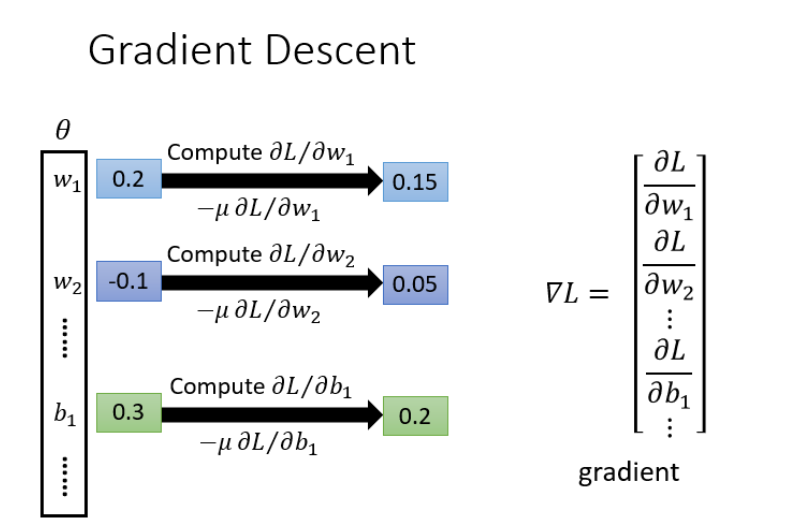
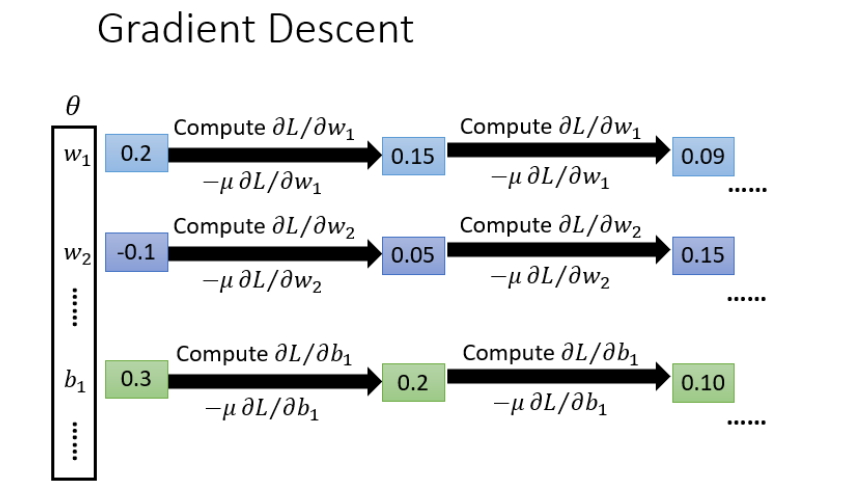
具体流程：\(\theta\) 是一组包含权重和偏差的参数集合，随机找一个初试值，接下来计算一下每个参数对应的偏微分，得到一个偏微分的集合\(\nabla L\)就是梯度，有了这些偏微分，就可以不断更新梯度得到新的参数，这样不断反复进行，就可以得到最好的参数使得损失函数最小。
反向传播
在神经网络钟计算损失最好的方法就是反向传播，可以利用TensorFlow, theano, Pytorch等等框架计算。
- 损失函数(Loss function) 是定义在单个训练样本上的，也就是算一个样本的误差，
- 代价函数(Cost function)是定义在整个训练集上的，也就是所有样本的误差的总和的平均。
- 总体损失函数(Total loss function)是定义在整个训练集上面的，也就是所有样本的误差总和，也就是评估我们反向传播需要最小化的值。
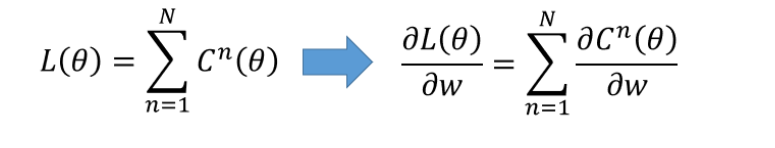
对一个神经元(Neuron)进行分析
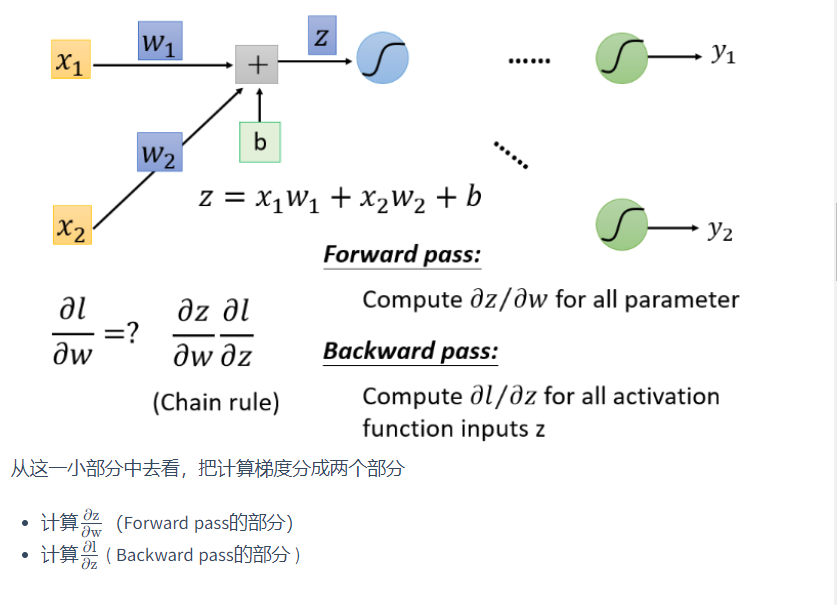
前向部分
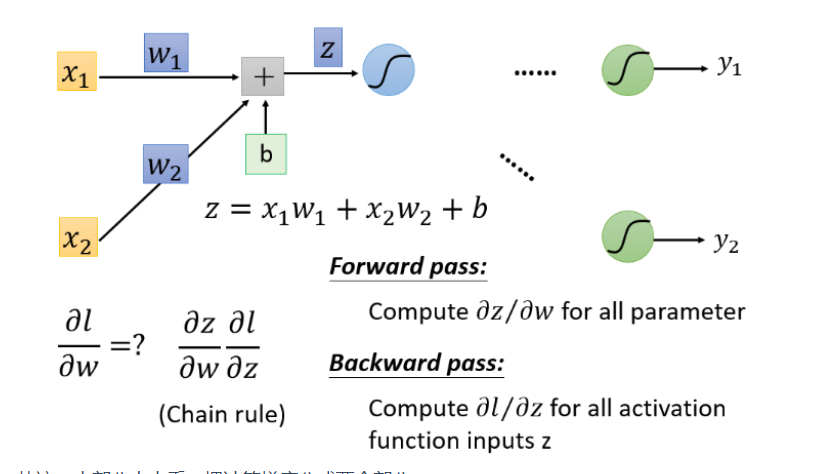
根据微分原理，\(\frac{\partial z}{\partial w_1} = x_1\), \(\frac{\partial z}{\partial w_2}=x_2\)
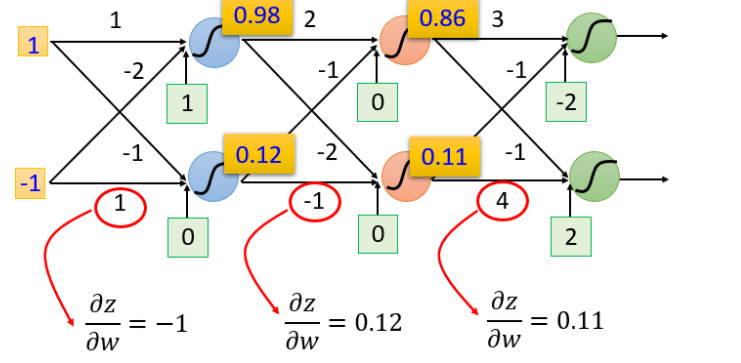
反向部分
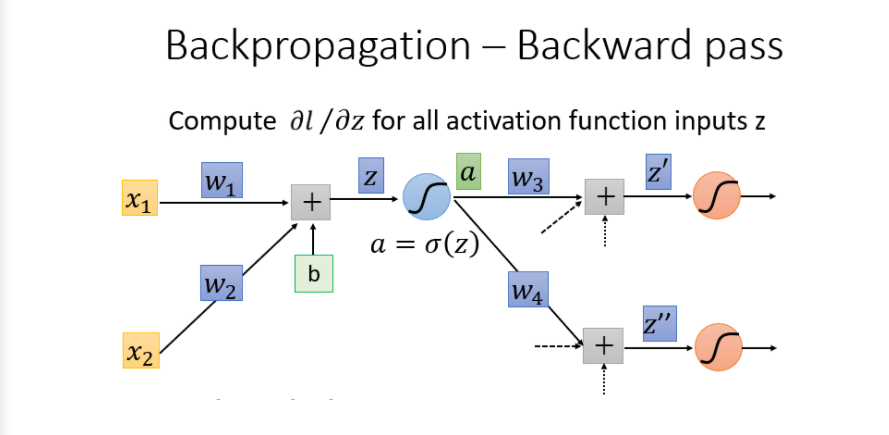
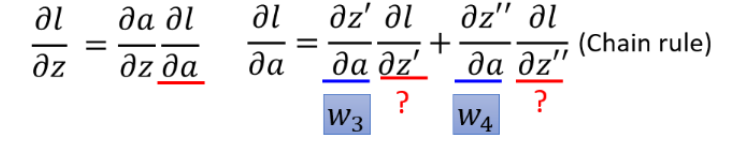
最终结果：
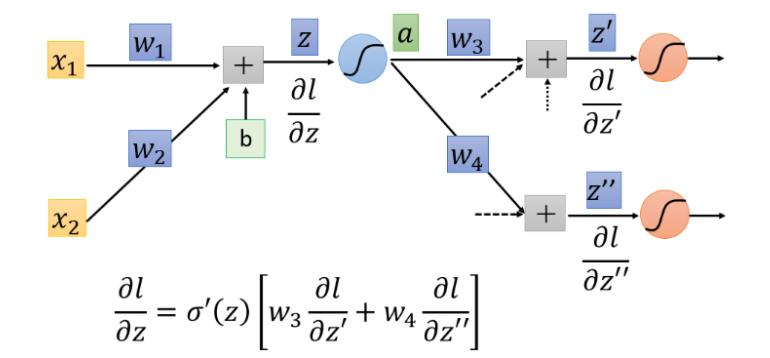
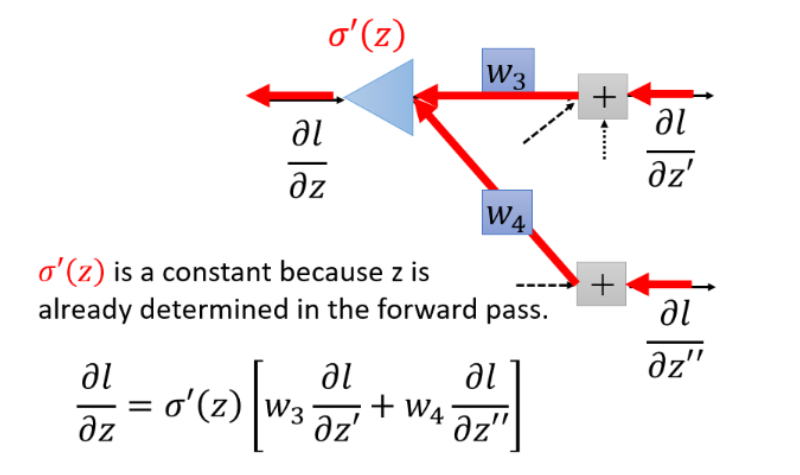
理解：但是你可以想象从另外一个角度看这个事情，现在有另外一个神经元，把forward的过程逆向过来，
其中\(\sigma'(z)\)是常数，因为它在向前传播的时候就已经确定了。
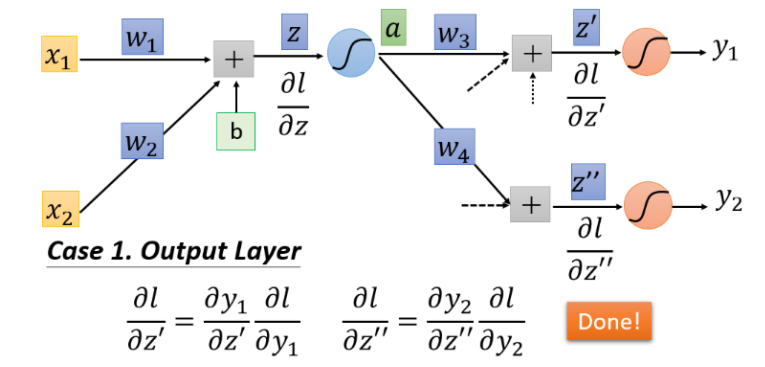
若\(\frac{\partial l}{\partial z'}\)和\(\frac{\partial l}{\partial z''}\)是最后一层隐藏层，那么直接计算就可以得到结果
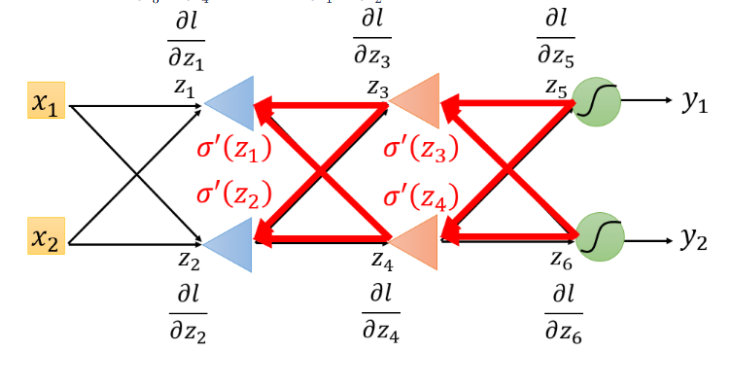
若\(\frac{\partial l}{\partial z'}\)和\(\frac{\partial l}{\partial z''}\)最后一层隐藏层，则需要一直往后通过链式法则计算下去
总结
我们的目标就是计算\(\frac{\partial z}{\partial w}\)(Forward pass部分)和计算\(\frac{\partial l}{\patial z}\)(Backward pass的部分)，然后将\(\frac{\partial z}{\partial w}\)和\(\frac{\partial l}{\patial z}\)相乘就可以得到
\(\frac{\partial l}{\partial w}\)，就可以得到神经网络中所有的参数，然后用梯度下降不断更新，得到损失最小函数。
