KMP算法学习笔记
KMP算法学习笔记
KMP算法的关键在于利用已经匹配过的字符串的信息——前缀和后缀。
一、基本定义
前缀：字符串s从下标0开始的一个子串。如s = "abcd"，则其前缀有"a", "ab", "abc".
后缀：字符串s以最后一个字符结尾的一个子串。如s = "abcd",则其后缀有"d", "cd", "bcd".
子串：substring[i : j] (i < j)，表示从下标 i 到 j - 1的子串（不包括下标 j）。
注意：字符串s的前缀和后缀都不包括s本身！
二、部分匹配表PMT
（一）最长共同前后缀
如现有字符串s = "ababab".
则s的前缀集合为{"a", "ab", "aba", "abab", "ababa"}；后缀集合为{"b", "ab", "bab", "abab", "babab"}；前缀集合和后缀集合的交集为{"ab", "abab"}。
最长共同前后缀为前缀集合和后缀集合的交集中，长度最长的字符串。在本例中，为"abab"。
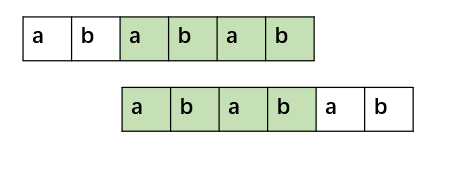
最长共同前后缀的实际意义就是某个字符串的后一部分和前一部分相同且长度最长。从最长共同前后缀的意义也可以看出为什么字符串s的前缀和后缀不包括s本身，因为如果包含s本身，那么最长共同前后缀就一定是s了，这样就没有意义了。
（二）PMT（Partial Match Table）
对于字符串s，PMT是这样一个数组，其长度和s的长度相同。PMT中的每个值，即PMT[i]，是s的子串s[0: i + 1]（即从下标0到i的子串，不包括下标i + 1），这个子串的最长共同前后缀的长度。
对于s="ababab"，PMT[3]是子串"abab"的最长共同前后缀的长度，为2.
因此，对于每个字符串s，都可以求得相应的PMT。
（三）PMT与KMP算法
PMT与KMP算法到底有什么关系呢？
首先前面提到，KMP算法的关键在于利用已经匹配的字符串的前后缀信息。那么，这种“利用”又是什么呢？
假设我们有待匹配串（main）和模式串（pattern），当前匹配情况如下（绿色部分已经成功匹配）。
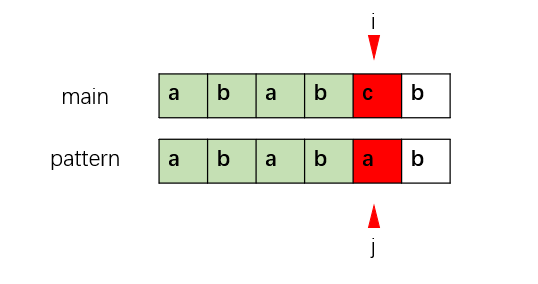
此时，当我们匹配到下标4时，发现'c' 和 'a' 不匹配。朴素的匹配法是将i移到下标1，j移到下标0重新匹配。但是我们可以利用前面匹配成功的字符串"abab"的信息来优化。
"abab"的最长共同前后缀为"ab"（即"ab"既是"abab"的前缀，也是"abab"的后缀），因此，在main串中取"ab"为后缀，在pattern串中取"ab"为前缀（图中蓝色部分），那么此时main串的后缀一定与pattern串的前缀相同，我们利用前后缀的信息完成了这一部分的匹配，接下来只需比较main中后缀的下一位和pattern中前缀的下一位即可（即图中两个蓝色部分的下一位）。
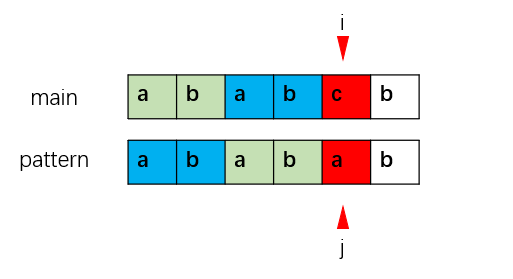
此时，i不变，j回溯至蓝色前缀的下一位，使得整个匹配的时间复杂度从O(m*n)降低至O(n)。(n = main.length, m = pattern.length)
这就是KMP算法利用前后缀的关键所在。
至此，我们可以总结出KMP算法的关键步骤（一些细节先略去）：
- 如果main[i] == pattern[j]，则i++, j++，继续比较下一位（和朴素匹配法相同）
- 如果main[i] != pattern[j]， 则i不必回溯，j回溯到已成功匹配串的最长共同前后缀作为前缀的下一位。
三、编程实现
（一）next数组
为了方便编程，我们将PMT变成一个next数组，next数组是PMT向右移动一位形成的数组，next[0] = -1.
PMT[i]的意义是substring[0 : i + 1]的最长共同前后缀的长度，则next[i]的物理意义即为substring[0 : i]的最长共同前后缀的长度，也就是0到 i - 1的子串的最长共同前后缀的长度。
为什么要将PMT转化为next数组呢？原因非常直接，仅仅是为了方便编程。主要方便在以下几点：
- next[i]是0到 i - 1的子串的最长共同前后缀的长度，因此当下标i不匹配而0到 i - 1匹配时，可以直接通过next[i]获取信息。
- next[i]是最长共同前后缀的长度，假设长度为3，则pattern的j指针回溯到下标3，正好是共同前后缀作为前缀的下一个下标。
- next[0] = -1，只有当 j = 0 匹配失败时才会读取next[0] = -1，此时需要特殊处理（即第一个字符就不匹配了，则 i++, j = 0）。
因此，KMP的主要代码如下：
public int KMP(String main, String pattern) {
int[] next = getNext(pattern);
int i,j;
i = j = 0;
while(i < main.length() && j < pattern.length()) {
if(j == -1 || main.charAt(i) == pattern.charAt(j)) { // 匹配或j = -1的特殊情况
i++;
j++;
}
else { // 不匹配
j = next[j];
}
}
if(j == pattern.length()) return i - j; // 返回匹配串的第一个字符的下标
return -1;
}
（二）获取next数组
获取next数组，需要求substring[0 : i]的最长共同前后缀的长度。在计算过程中，本质上就是用下面pattern的前缀去匹配上面pattern的后缀的过程，因为我们要找最长共同前后缀。
需要注意的是，在作为main的pattern中，i从坐标1开始匹配。
如果匹配成功，则 i++, j++，以获取更长的共同前后缀，并更新next[i + 1] = j + 1.（i + 1是因为next相对PMT右移了一位， j + 1是因为下标加1才为长度）
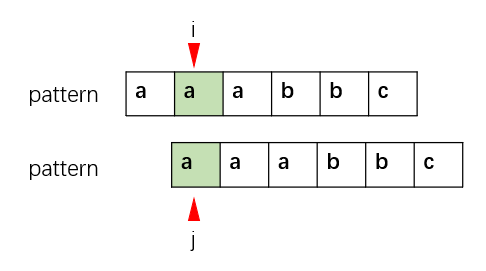
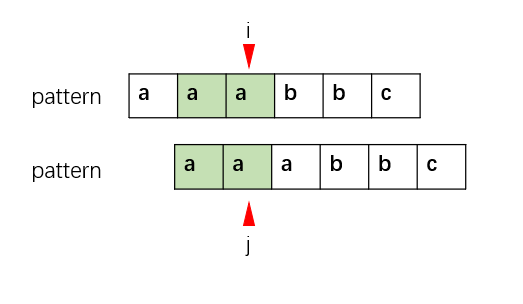
而当不匹配时，j就需要回溯（这里就已经用到了KMP的思想），利用前面已匹配部分（绿色部分）的前后缀信息来回溯 j = next[j]，通过获取共同前后缀来尝试扩展前缀和后缀。
需要注意的是，当next[j] == -1时，意味着pattern中的第一位也无法匹配，此时不存在共同前后缀，next[i + 1] = 0，i++, j = 0继续进行后续计算。
获取next数组的代码如下：
public int[] getNext(String pattern) {
int[] next = new int[pattern.length()];
int i,j;
next[0] = -1;
i = 1;
j = 0;
while (i < pattern.length()) {
if(j == -1 || pattern.charAt(i) == pattern.charAt(j)) {
i++;
j++;
if(i < pattern.length()) next[i] = j; // 这里先i++是因为next相对PMT右移一位，j++是因为长度为下标+1
}
else {
j = next[j]; // 不匹配 j回溯
}
}
return next;
}
