浅谈Aho-Corasick automaton(AC自动机)
Aho-Corasick automaton是什么?
要学会AC自动机,我们必须知道什么是Trie,也就是字典树。Trie树,又称单词查找树或键树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。
首先我们要知道trie,而且要知道KMP,这样就可以学AC自动机了!
其实AC自动机就是trie和KMP的结合体。主要构建trie后使用KMP的主导思想构建fail边,每次匹配与KMP相似。
下面我们看看如何构造fail边。
fail边就是类似KMP中的next数组,在失配的时候能够指向的地方。
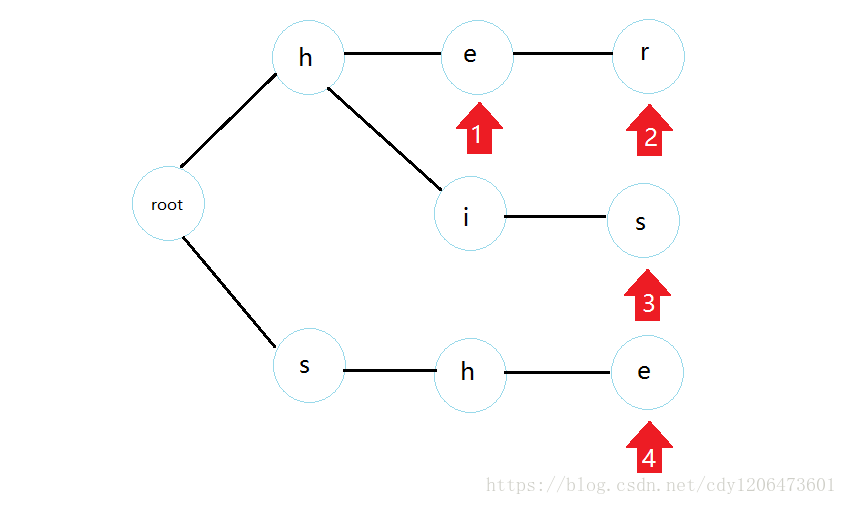
这就是一颗trie树,那么我们应该怎么去连fail边呢?
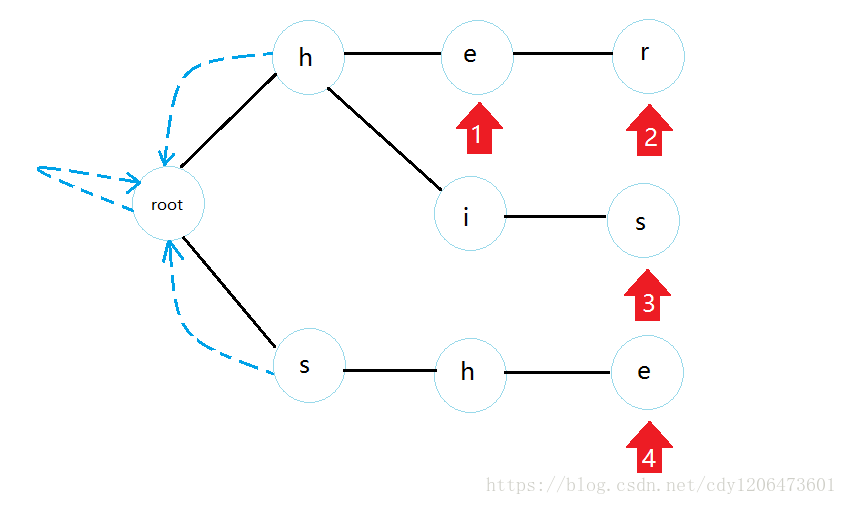
首先我们知道root的fail边是连向自己的,而且所有与root直接相连的点fail都指向root。
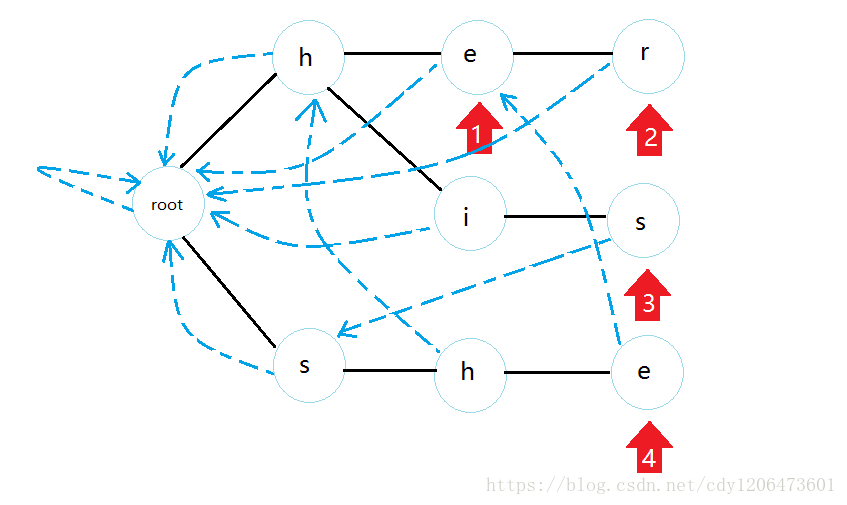
然后每个点,看看自己父亲的fail边指向的位置的点是否有一个与它长的一样的儿子,如果有,那么连上,否则继续找fail边,直到root为止(注意这个过程我们用bfs实现)。所以最终连完的fail边就是这样:
这样我们只需要每一位去匹配就好了。
有人问,怎么匹配:
举个栗子:
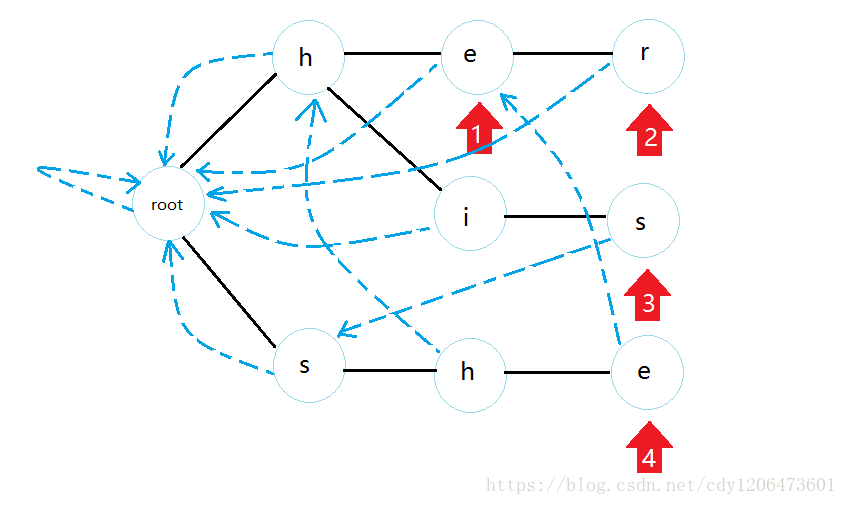
用上面的图:
假设原串是:ahershe,这棵trie上有his,her,he,she。
我们从root开始,先查找root点有没有当前字母的儿子a,有那么指针x指到h点上,这样一直匹配;如果没有,那么就直接跳到当前点的fail边上,这样保证前面匹配的全都是相同的,直到有这样的儿子或者已经到了root并且没有这样的儿子为止。
注意每跳一个点就必须从当前点遍历一遍它的fail边直到root的边集,就是说沿着fail边跳一直到root为止,这是为了避免当前点没有被标记,但是在它fail边到达root的路径上有被标记的点。
Exanple
【GDOI2013模拟4】贴瓷砖
Description
A镇的主街是由N个小写字母构成,镇长准备在上面贴瓷砖,瓷砖一共有M种,第i种上面有Li个小写字母,瓷砖不能旋转也不能被分割开来,瓷砖只能贴在跟它身上的字母完全一样的地方,允许瓷砖重叠,并且同一种瓷砖的数量是无穷的。
问街道有多少字母(地方)不能被瓷砖覆盖。
Input
第一行输入街道长度N(1<=N<=300,000)。
第二行输入N个英文小写字母描述街道的情况。
第三行输入M(1<=M<=5000),表示瓷砖的种类。
接下来M行,每行描述一种瓷砖,长度为Li(1<=Li<=5000),全部由小写字母构成。
Output
输出有多少个地方不能被瓷砖覆盖。
Sample Input
输入1:
6
abcbab
2
cb
cbab
输入2:
4
abab
2
bac
baba
输入3:
6
abcabc
2
abca
cab
Sample Output
输出1:
2
输出2:
4
输出3:
1
Data Constraint
N(1<=N<=300,000)
Solution
我们把原字符串每一位都进行匹配,然后首先预处理出trie中每一个点对应所有fail边中最大的长度,然后匹配的时候记录下每一位中能够覆盖到的最大长度,最后用线段树维护(当然你可以直接用差分约束)。
Code
#include<cstdio>
#include<iostream>
#include<cstring>
#define mo 1000010
using namespace std;
struct Moon{int fail,num,maxl;}point[4000010];
int son[4000010][27];
int lengt_max[300010],length[300010];
char s[300010],ch[300010];
int len,n,root,sz;
int d[mo];
int f[300010*4],tag[300010*4];
void make_trie(char s1[300010],int len1,int t,int x,int id)
{
if(t>len1)
{
point[x].num=id;
point[x].maxl=length[id];
return;
}
if(!son[x][s1[t]-96])
{
son[x][s1[t]-96]=++sz;
++son[x][0];
make_trie(s1,len1,t+1,sz,id);
}
else make_trie(s1,len1,t+1,son[x][s1[t]-96],id);
}
void build_fail()
{
int i,x,k,head=0,tail=0;
for (i=1;i<=26&&tail<son[root][0];++i)
if(son[root][i])
{
d[++tail]=son[root][i];
point[son[root][i]].fail=root;
}
while(head!=tail)
{
head=head%mo+1;
x=d[head];
if(!son[x][0]) continue;
for (i=1;i<=26;++i)
if(son[x][i])
{
tail=tail%mo+1;
d[tail]=son[x][i];
k=point[x].fail;
while(k!=root)
{
if(son[k][i]) break;
k=point[k].fail;
if(k==root&&!son[k][i]) break;
}
if(son[k][i]) point[son[x][i]].fail=son[k][i];
else point[son[x][i]].fail=root;
point[son[x][i]].maxl=max(point[son[x][i]].maxl,point[point[son[x][i]].fail].maxl);
}
}
}
void Check()
{
int x=root,k;
for (int i=1;i<=len;)
{
if(son[x][s[i]-96])
{
x=son[x][s[i]-96];
lengt_max[i]=max(lengt_max[i],point[x].maxl);
++i;
}
else x=point[x].fail;
if(x==root&&!son[x][s[i]-96]) ++i;
}
}
void change(int v,int l,int r,int x,int y)
{
if(l==x&&r==y)
{
tag[v]=1;
f[v]=r-l+1;
return;
}
int mid=(l+r)/2;
if(tag[v])
{
tag[v*2]=1,f[v*2]=mid-l+1;
tag[v*2+1]=1,f[v*2+1]=r-mid;
tag[v]=0;
}
if(y<=mid) change(v*2,l,mid,x,y);
else if(x>mid) change(v*2+1,mid+1,r,x,y);
else change(v*2,l,mid,x,mid),change(v*2+1,mid+1,r,mid+1,y);
f[v]=f[v*2]+f[v*2+1];
}
int main()
{
scanf("%d",&len);
scanf("%s",s+1);
scanf("%d",&n);
int i,j;
root=sz=point[1].fail=1;
for (i=1;i<=n;++i)
{
scanf("%s",ch+1);
length[i]=strlen(ch+1);
make_trie(ch,length[i],1,root,i);
}
build_fail();
Check();
for (i=1;i<=len;++i)
if(lengt_max[i]) change(1,1,len,i-lengt_max[i]+1,i);
printf("%d\n",len-f[1]);
}