浅谈Suffix Automaton（后缀自动机）

这是一个强大的automaton——Suffix Automaton==>我学过最强大，最牛犇，最难理解的自动机

现在给你一个问题:

给定一个字符串，要求这个字符串所有子串出现的次数分别是多少

朴素算法

①枚举左端点，枚举右端点，用hash记录一下，统计个数。(注意最好双hash，保证正确率)
预计时间复杂度：\(O(n^2)\)
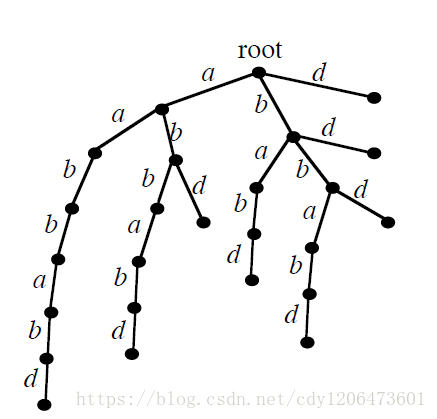
②可以直接开trie记录，以所有后缀建，就好像这样：aabbabd

每次建的时候就记录每个地方的次数，因为有\(n^2\)个点，那么时间复杂度也就是\(O(n^2)\)

\(n^2\)复杂度很优秀，但是...

n<=100000啊啊啊啊啊....

这样做不了，怎么办？！

这时我们引进Suffix Automaton（后缀自动机）

（集中精神，前方高能）

后缀自动机定义

一个串\(S\)的后缀自动机\((SAM)\)是一个有限状态自动机\((DFA)\)，它能且只能接受所有\(S\)的后缀(当然，它能做的事情远远不仅限于后缀).

后缀自动机其实是一个\(DAG\)(有向无环图)，其中顶点是状态，边代表了状态之间的转移.

某一状态\(S\)被称为初始状态，由它能够到达其余所有状态.

自动机的所有转移，都是一条有向边，且都被某种符号标记，从某一状态出发的所有转移必须拥有不同的标记.

一个状态被称为终止状态，表示如果我们从初始状态\(S\)经任意一条路径走到某一终止状态，并顺序写出经过边的标记，得到的字符串必定是原串的后缀.

在符合上述条件的所有自动机中，后缀自动机拥有最少的状态与转移，并且后缀自动机的状态数以及转移数都是\(O(|S|)\)的.

Pre的定义

可以说，pre是后缀自动机中最核心的东西，也是最难懂的部分。所以认真看！
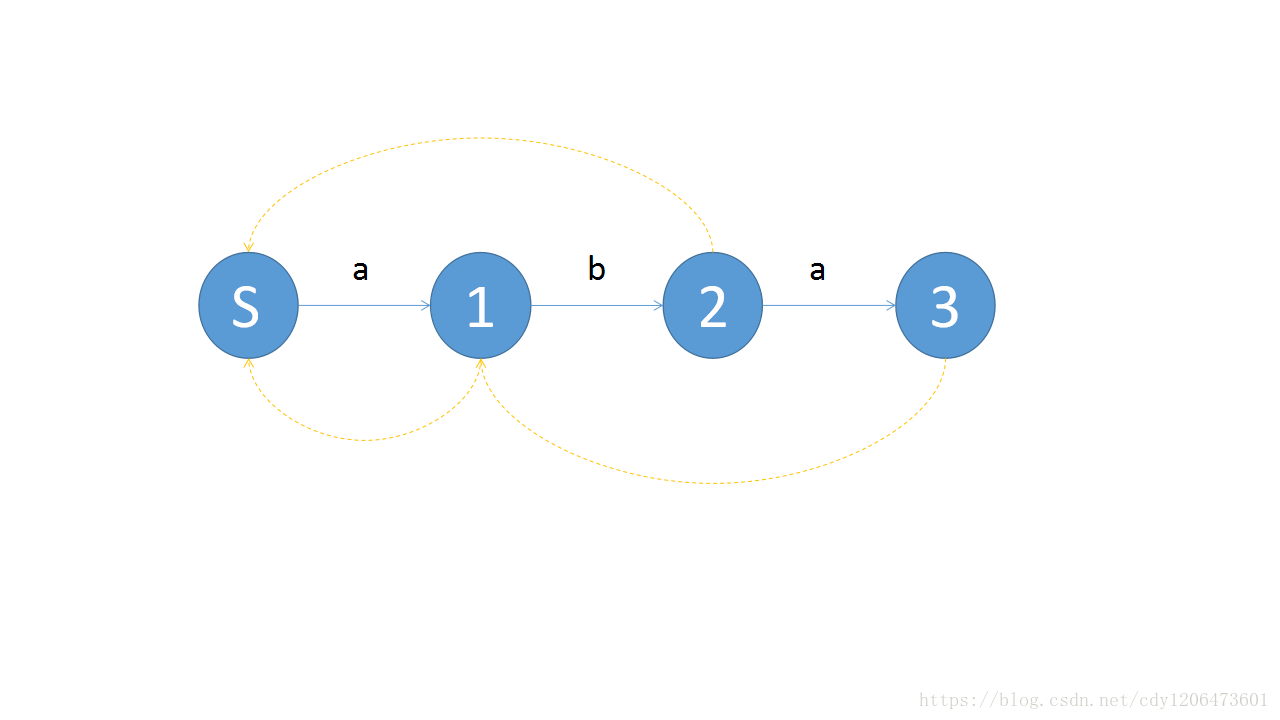
pre[x]表示字符串[S_{x]的最长后缀[S}pre[x]]的右端点，例如：

绿色的虚线表示pre边。很显然我们可以发现3的pre边连向的是[S_{3]的最长后缀[S}1]的右端点1。

Pre的连边

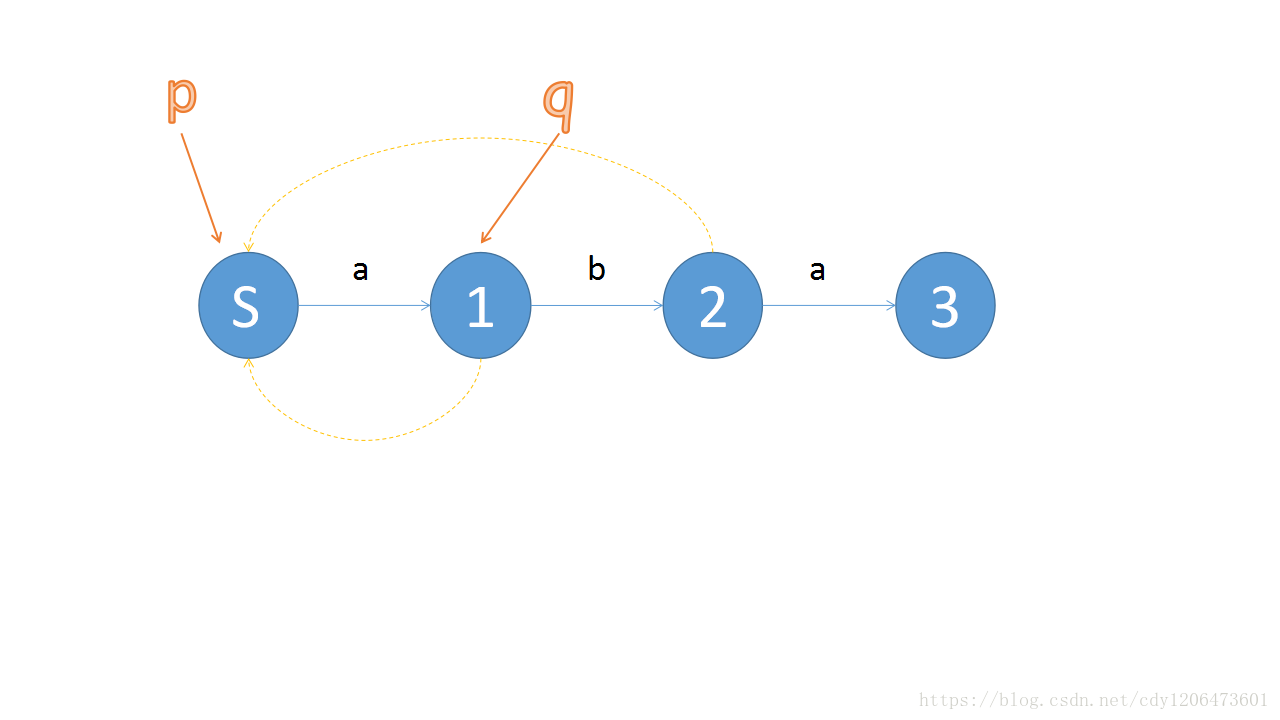
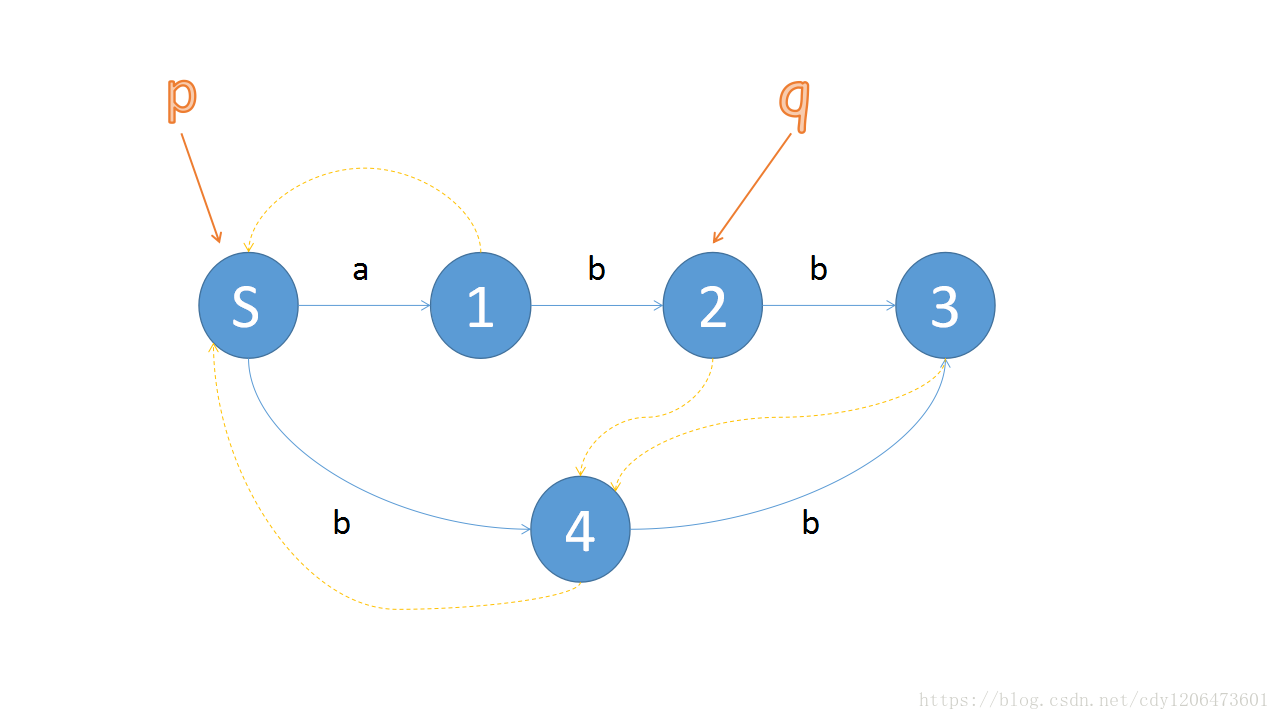
对于刚刚加入的now点，寻找las的pre边，如果没有一条与当前新加的这条边相同的边就加上一条这样的边，直到找到一个有与当前新加的这条边相同的边为止。然后分为两种情况：我们设当前找到的这个点为p，它连向的儿子为q。

①如果p，q两点距离为1，那么就可以直接把当前新节点的pre边指向q。
②如果p，q两点距离大于1，我们会发现如果把当前新节点的pre边指向q，不符合[S_q]为[Snow]的后缀（如下图）

（ab并不是abb的后缀）
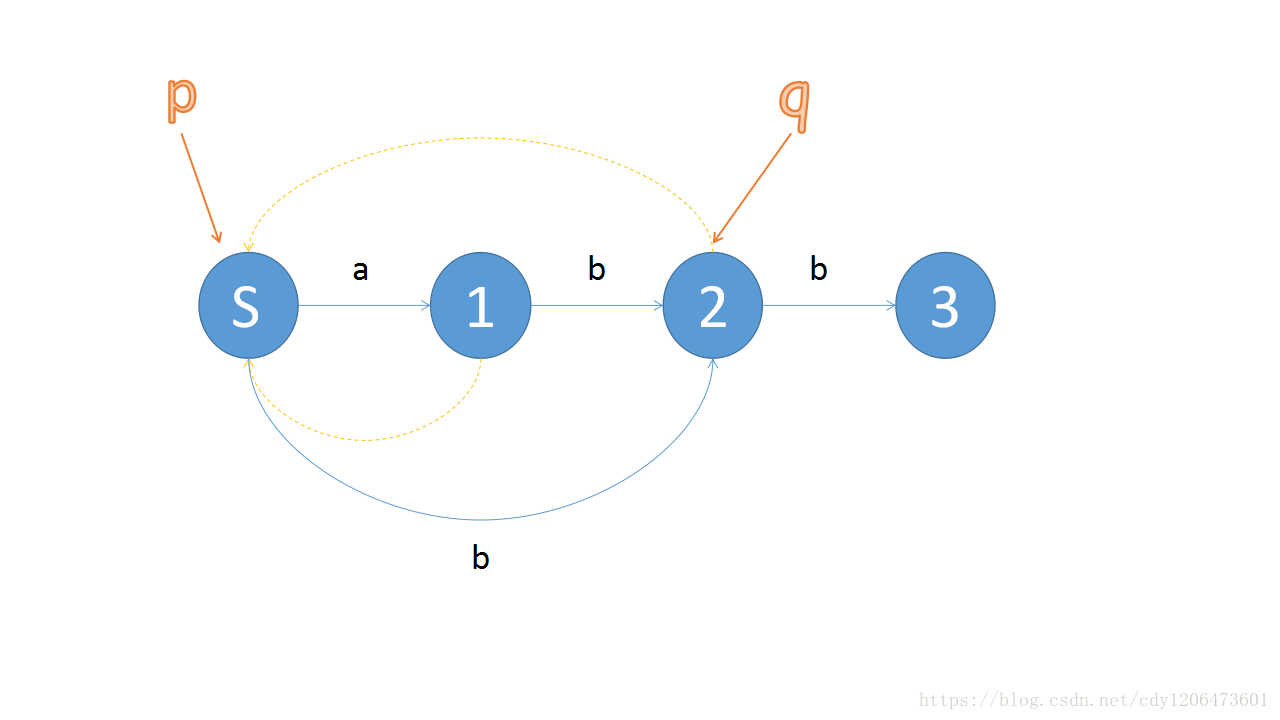
我们分析这样做错误的原因，因为我们把原串中的ab当成了b（就是连在下面的那条边），所以把ab误认为成了abb的后缀，那么我们想，我们呢原来是想连b为后缀的，所以这是我们需要进行加点操作。

加点操作

我们在p以后加入一个点，与p及以前所有与q用当前符号为边相连的点，与新加入的点连上一条与当前符号相同的边，例如上图是b，因为这个点在原串中是不存在的，它只是q的一个分身，所以q指出去的所有边它也都要连，然后新加的点的pre边自然就变成了q原来的pre边，然后q和now的pre边也就指向了当前新加节点：

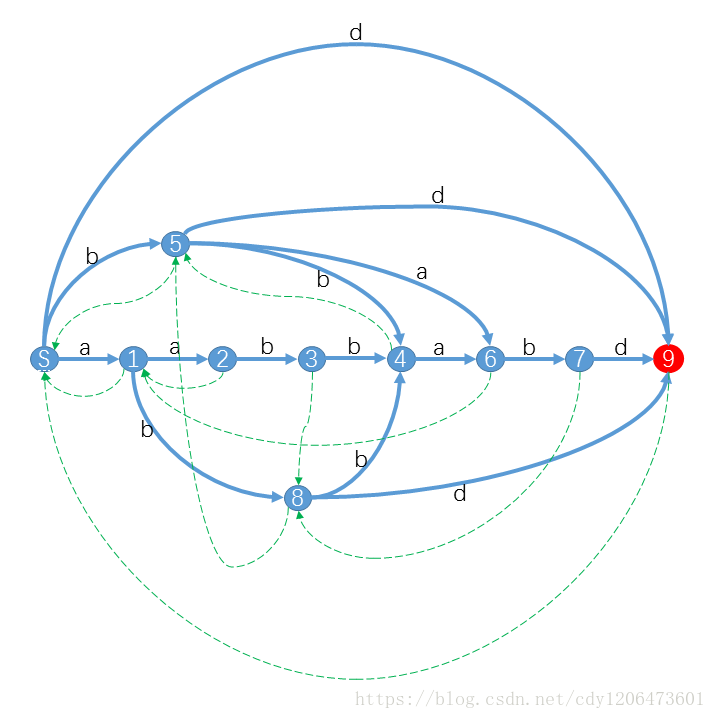
对于“aabbabd”来说它的自动机长这样：

时间复杂度

时间复杂度是：\(O(n)\).
最大的状态数是2n-1，因为除了前面三个点，后面的所有点都可以加点。

应用

1.给定字符串T，每次询问一个p，问p是否为T的子串.

• 对T建一个后缀自动机.
• 每次询问就从初始状态ss开始走，然后沿着询问的字符串走.
• 时间复杂度\(O(|T|+∑ |p|)O(|T|+∑ |p| )\)

2.给定字符串S，问它有多少不同的子串.

• 还是先建一个后缀自动机.
• 那么对于后缀自动机中的任何一条路径，都是一个不同的子串.
• 所以答案就是从S开始出发的不同路径数.

3.给定字符串S，每次询问S的所有不同子串中字典序第k小.

• 和前两问类似，我们只需要处理从一个状态开始，每种字符的路径条数.
• 然后从起点S一直找就好了.

4.给定字符串S，找到和它循环同构的字典序最小的字符串.

• 我们对字符串S+S做一个后缀自动机，然后贪心的找字典序最小就好啦~

5.给定多个字符串，求它们的最长公共子串.

• 思考...

模板Code

#include<cstdio>
#include<iostream>
#include<cstring>
#define maxN 2000010
using namespace std;
int son[maxN][27],pre[maxN],len[maxN],sum[maxN];
int sz,las,lens,now,q,p;
char s[maxN];
void add(int x)
{
	len[++sz]=len[las]+1,sum[sz]=1,now=sz;
	for (p=las;p&&!son[p][x];p=pre[p]) son[p][x]=now;
	if(p)
	{
		q=son[p][x];
		if(len[q]>1+len[p])
		{
			len[++sz]=len[p]+1;
			memcpy(son[sz],son[q],sizeof(son[q]));
			pre[sz]=pre[q];pre[q]=pre[now]=sz;
			for (;son[p][x]==q;p=pre[p]) son[p][x]=sz;
		}
		else pre[now]=q;
	}
	else pre[now]=1;
	las=now;
}
int main()
{
	scanf("%s",s+1);
	lens=strlen(s+1);sz=las=1;
	for (int i=1;i<=lens;++i) add(s[i]-96);
}