Datawhale编程——动态规划DP
0-1背包问题
问题:有n个物品,第i个物品价值为vi,重量为wi,其中vi和wi均为非负数,背包的容量为W,W为非负数。现需要考虑如何选择装入背包的物品,使装入背包的物品总价值最大。
针对这个经典的动态规划问题,先建立一个实例,如下表格:
| 物体编号i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 价值v | 4 | 5 | 10 | 11 | 13 |
| 重量w | 3 | 4 | 7 | 8 | 9 |
假设约束条件背包的最大承重\(W = 17\),且每个物体只能装一次,请问背包应该怎么装最好。
这一类问题依旧是两个关键:1.初始条件或者最小子问题最优解;2.递归定义式或状态转移方程。
这里最小子问题最优解应该就是,背包只选一个物品且在限定承重 W' 时所指向的最佳物体。这里 W' 可以为大于等于1的任意值。
那么状态转移方程应该就是,在当前给定限定承重条件下,从不同的承重组合选出一个最优解(每一个都是它在限定承重条件下得到的最优解)。用数学定义式可以如下:
其中dp[i][j]表示i件物品放入一个容量为j的背包可以获得的最大价值。这个式子不是很好理解,举个例子就很清楚了,如下。
比如当前背包容量是10,那我们可以有多种分配组合,比如9+1,以及7+3。其中dp[i-1][j]可以对应分配的9,dp[i-1][j-w(k)]可以对应分配的7;左边9所对应的1是再找不出适合装的东西了,右边7对应的3可以再装一个编号1。这个式子的意义就是,比较这两种组合其中的更佳者。
需要注意的是,不一定永远是右边的更佳,有时候空间不全部利用反而能得到更加解。这就是动态规划的关键。
要是直接将动态规划的代码写出来,有时候可能很困难。可以先考虑用递归做,再将自顶向下的递归转化为自底向上的动态规划就好了。这里就不管这些,直接给出动态规划的代码了。
class ZeroByOnePack:
def __init__(self, list_v, list_w):
self.list_v = list_v
self.list_w = list_w
def dpPack(n, max_w):
V = self.list_v
W = self.list_w
dp = [0] * (max_w + 1) # 为了形式上好理解,只好浪费一部分空间
for i in range(n);
for j in range(W[i], max_w + 1):
dp[j] = max(dp[j], dp[j-W[i]]+V[i])
return dp[max_w]
这里只用一维数组,节省内存空间。
leetcode 132
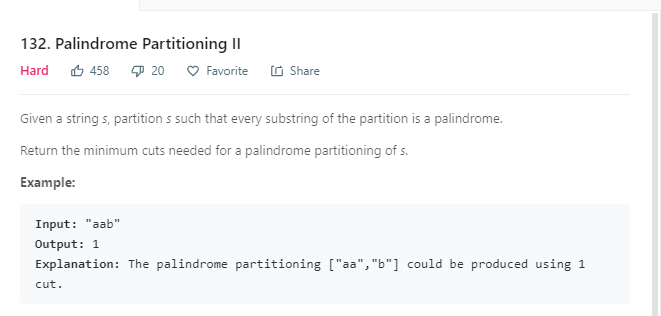
代码实现
作业限制了用动态规划,但其实这道题不用动态规划也可以做。
class Solution(object):
def minCut(self, s):
"""
:type s: str
:rtype: int
"""
cut = [x for x in range(-1,len(s))]
for i in range(0,len(s)):
for j in range(i,len(s)):
if s[i:j] == s[j:i:-1]:
cut[j+1] = min(cut[j+1],cut[i]+1)
return cut[-1]
当然,这个性能是很差的,时间复杂度应该达到了O(n3)?如果用动态规划的话,时间复杂度只要O(n2)。
class Solution:
def minCut(self, s):
"""
:type s: str
:rtype: int
This can be solved by:
cut[end] is the minimum of cut[st-1] + 1 (st <= end) if [st, end] is palindrome
a b a | c c
st end
st-1 | [st, end] is palindrome
cut(st-1) + 1
"""
n = len(s)
cut = [0] * n
pal = [[False] * n for row in range(n)]
for end in range(n):
min_cut = end
for st in range(end + 1):
if s[st] == s[end] and (end - st <= 2 or pal[st+1][end-1]):
pal[st][end] = True
min_cut = 0 if st == 0 else min(min_cut, cut[st-1] + 1)
cut[end] = min_cut
return cut[n-1]
代码不是自己写的。我只能根据简单的思路写出递归的算法,但是这道题卡了递归的边界。也许将递归算法改进成备忘录方法会更好点,这个留待以后验证了。



