真·浅谈treap树

treap树是一种平衡树，它有平衡树的性质，满足堆的性质，是二叉搜索树，但是我们需要维护他

为什么满足堆的性质？因为每个节点还有一个随机权值，按照随机权值维持这个堆（树），可以用O(logn)的复杂度维护他。树的期望深度是log n。

平衡树是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。权值：右儿子大于爸爸大于左儿子。

 

那么如何维护他呢？

我们来看看维护treap树的几个操作。

1.左旋右旋：

旋转是什么？看图：

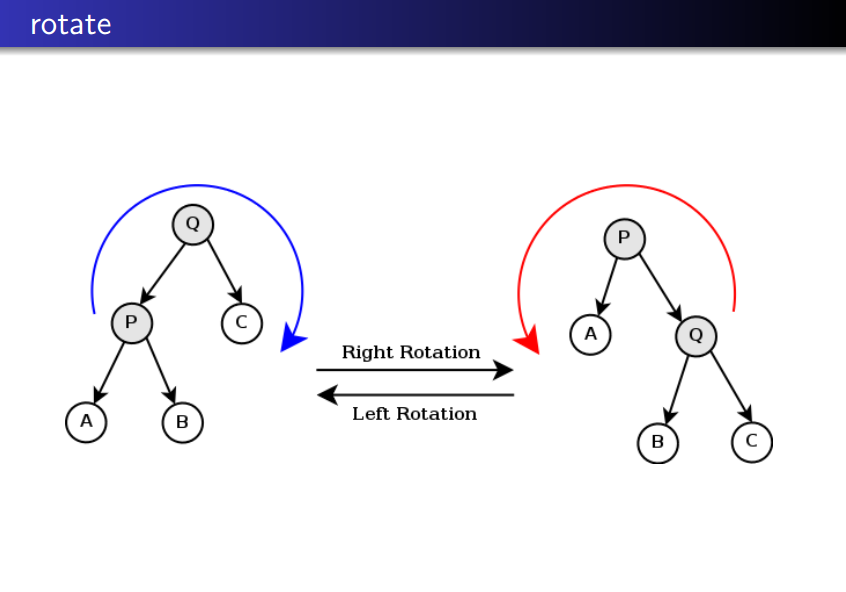
把父亲和他左(右)儿子及其各子树调换(反了！)

左旋：左儿子上窜（爸爸的左儿子换成儿子的右儿子，儿子的右儿子换成爸爸）

右旋：右儿子上窜（爸爸的右儿子换成儿子的左儿子，儿子的左儿子换成爸爸）

左旋右旋看上去没有用，但是他是服务于插入和删除操作的。

代码：

void update(int cur){
    sz[cur] = sz[lc[cur]] + sz[rc[cur]] + 1;
}

void right_rotate(int &Q){
    int P = lc[Q];
    lc[Q] = rc[P];            
    rc[P] = Q;                //爸爸的左儿子换成儿子的右儿子，儿子的右儿子换成爸爸 
    update(Q);                //更新右子树大小 
    update(P);                //更新左子树大小 
    Q = P;                    //把Q换成P 
}

void left_rotate(int &Q){
    int P = rc[Q];
    rc[Q] = lc[P];
    lc[P] = Q;
    update(Q);
    update(P);
    Q = P;
}

2.插入

　　插入就需要左旋右旋了，因为我们既维持treap其平衡树的性质，也要维持他堆的性质。

void insert(int &cur, int v){
    if(!cur)
    {
        cur = ++cnt;            //新加点的编号 
        V[cnt] = v;                //把权值赋给它 
        R[cnt] = rand();        //给出点的随机权值 
        return;
    }
    if(v < V[cur])                //比较新加点与当前点的权值 
    {
        insert(lc[cur], v);        //把当前点放到他左儿子身上，递归下去 
        update(cur);            //更新子树大小 
        if(R[lc[cur]] < R[cur])    //保持堆的性质 
            right_rotate(cur);
    }
    else
    {
        insert(rc[cur], v);        //把当前点放到他左儿子身上，递归下去
        update(cur);            //更新子树大小
        if(R[rc[cur]] < R[cur])    //保持堆的性质 
            left_rotate(cur);
    }
}

3.删除

void del(int &cur, int v){//cur当前节点，v表示要删的点的权值 
    if(!cur)
        return;
    if(V[cur] == v)
    {
        if(lc[cur] && rc[cur])
        {
            left_rotate(cur);
            del(lc[cur], v);
        }
        else 
        {
            cur = lc[cur] | rc[cur];
            update(cur);
            return;
        }
    }
    else if(V[cur] > v)
        del(lc[cur], v);
    else 
        del(rc[cur], v);
    update(cur);
}

4.第k大，前驱，后继

这些都是递归求的。

比如前驱，如果当前点的权值小于要找的值，那么走它的右子树，直到当前点权值大于要找的值，找它的左子树，因为左子树比当前点权值小。

int find(int cur, int v)
{
    if(V[cur] == v)
        return 1;
    else if(V[cur] > v)
        return find(lc[cur], v);
    else
        return sz[lc[cur]] + 1 + find(rc[cur], v);
}
int pre(int cur,int v)
{
    if(!cur)
        return 0xefefefef;
    if(v < V[cur])
        return pre(lc[cur],v);
    return max(V[cur],pre(rc[cur],v));
    
}
int post(int cur,int v)
{
    if(!cur)
        return 0x7fffffff;
    if(v > V[cur])
        return post(rc[cur],v);
    return min(V[cur],post(lc[cur],v));
}

差不多就是这些……

洛谷板题：https://www.luogu.org/problemnew/show/P3369