强连通分量
强连通分量
定义
连通图:图中,任意的两个点互相可达。
强连通(
强连通图:有向图
强连通分量(
通俗的讲,强连通就是两个点互相可达,强连通图就是图种任意两个点互相可达,强连通分量是该图中,任意的一些点都不能和该强连通分量互相可达
弱连通:将有向图
弱连通图:有向图
如下图,
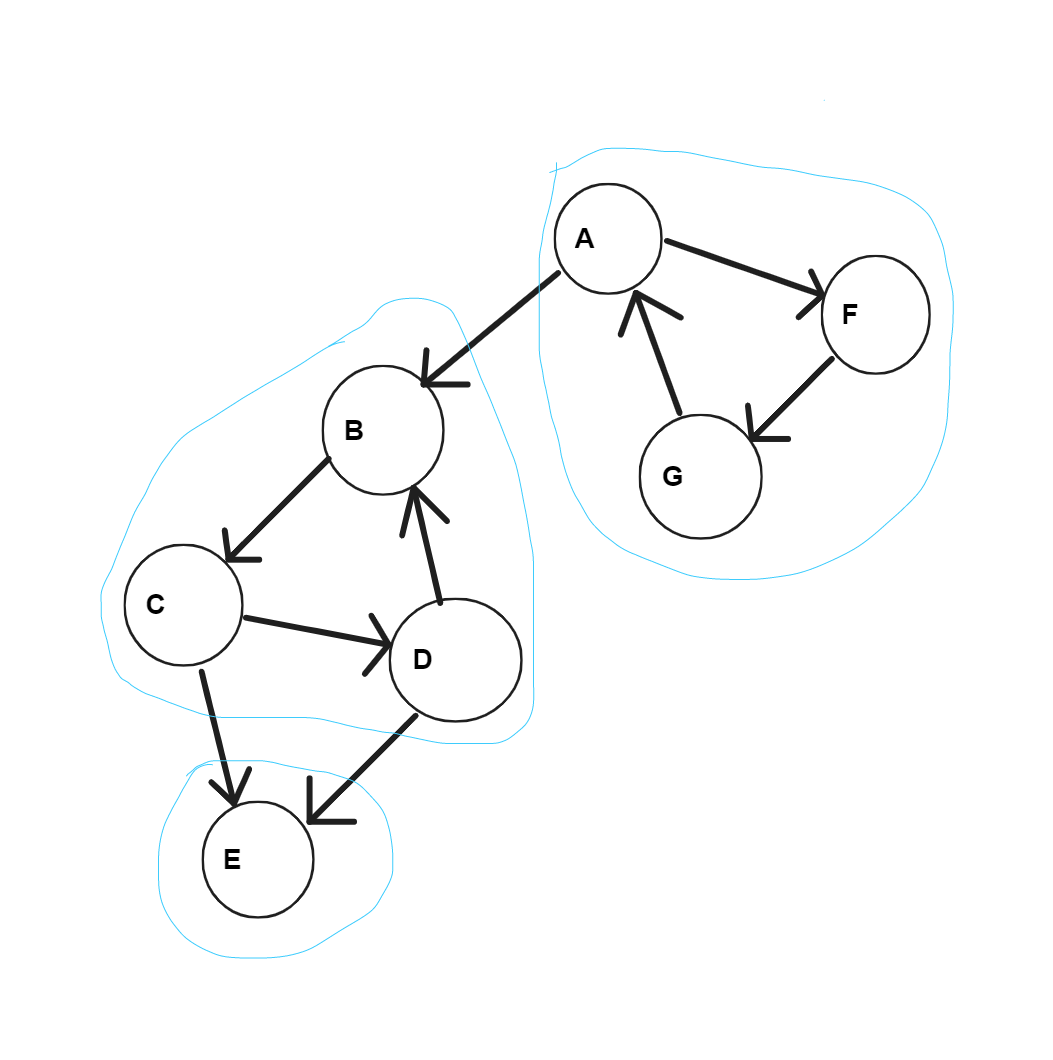
Tarjan 算法
在回溯时,若
算法伪代码
tarjan(u)
{
DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值
Stack.push(u) // 将节点u压入栈中
for each (u, v) in E // 枚举每一条边
if (v is not visted) // 如果节点v未被访问过
tarjan(v) // 继续向下找
Low[u] = min(Low[u], Low[v])
else if (v in S) // 如果节点v还在栈内
Low[u] = min(Low[u], DFN[v])
if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根
while (u != v)
v = S.pop // 将v退栈,为该强连通分量中一个顶点
print v
S.pop // 自己出栈
print u
}
具体例子,如下图
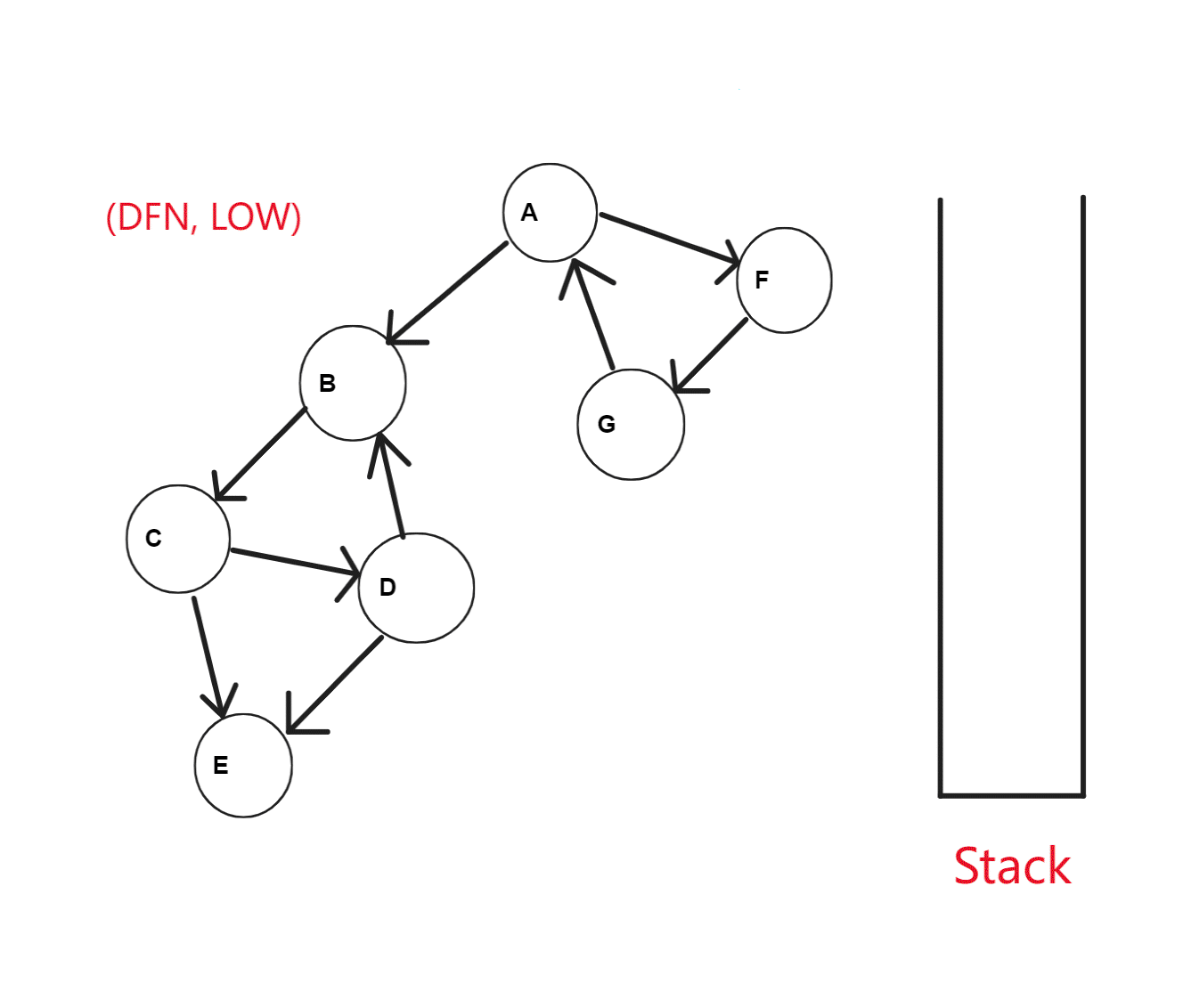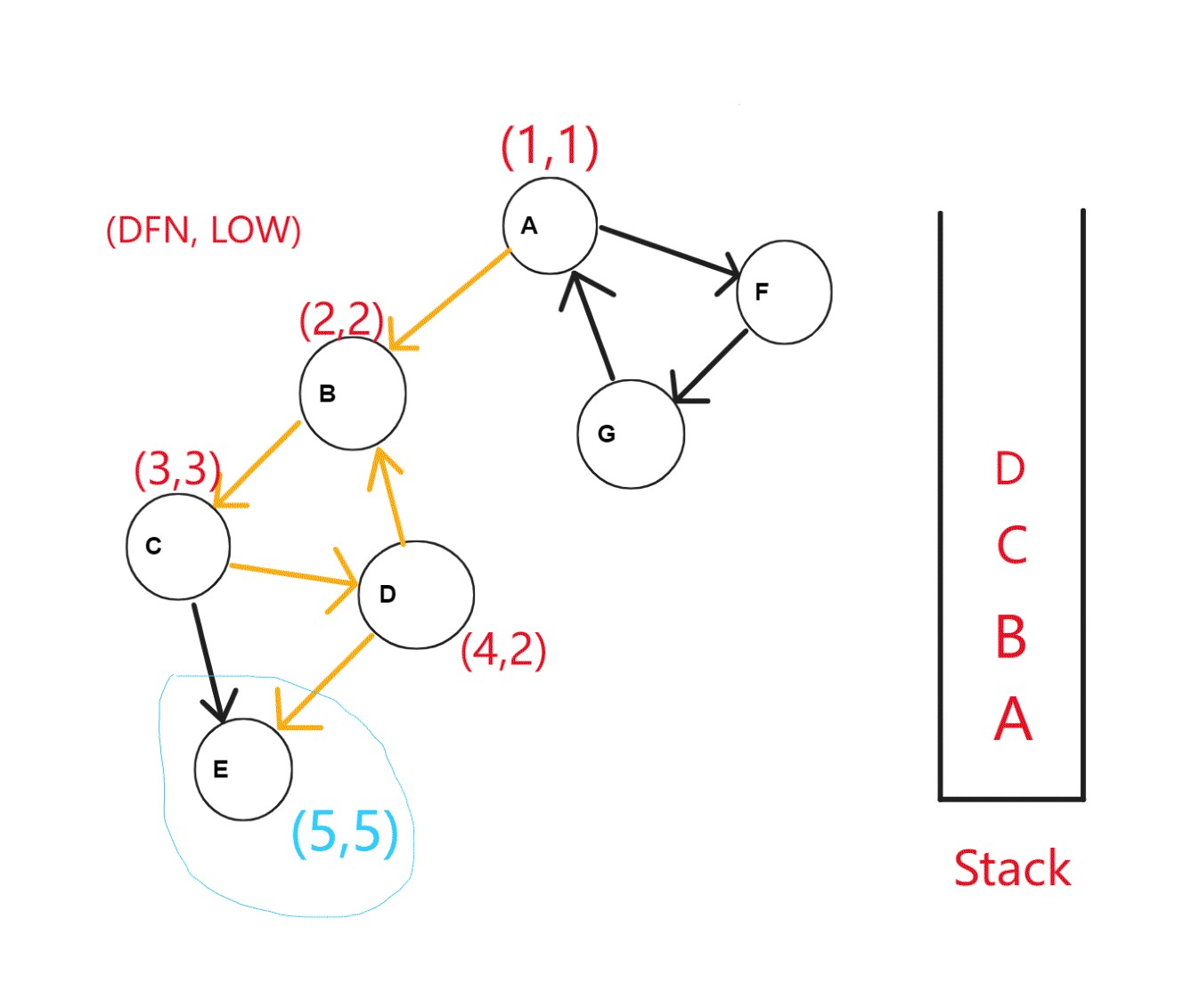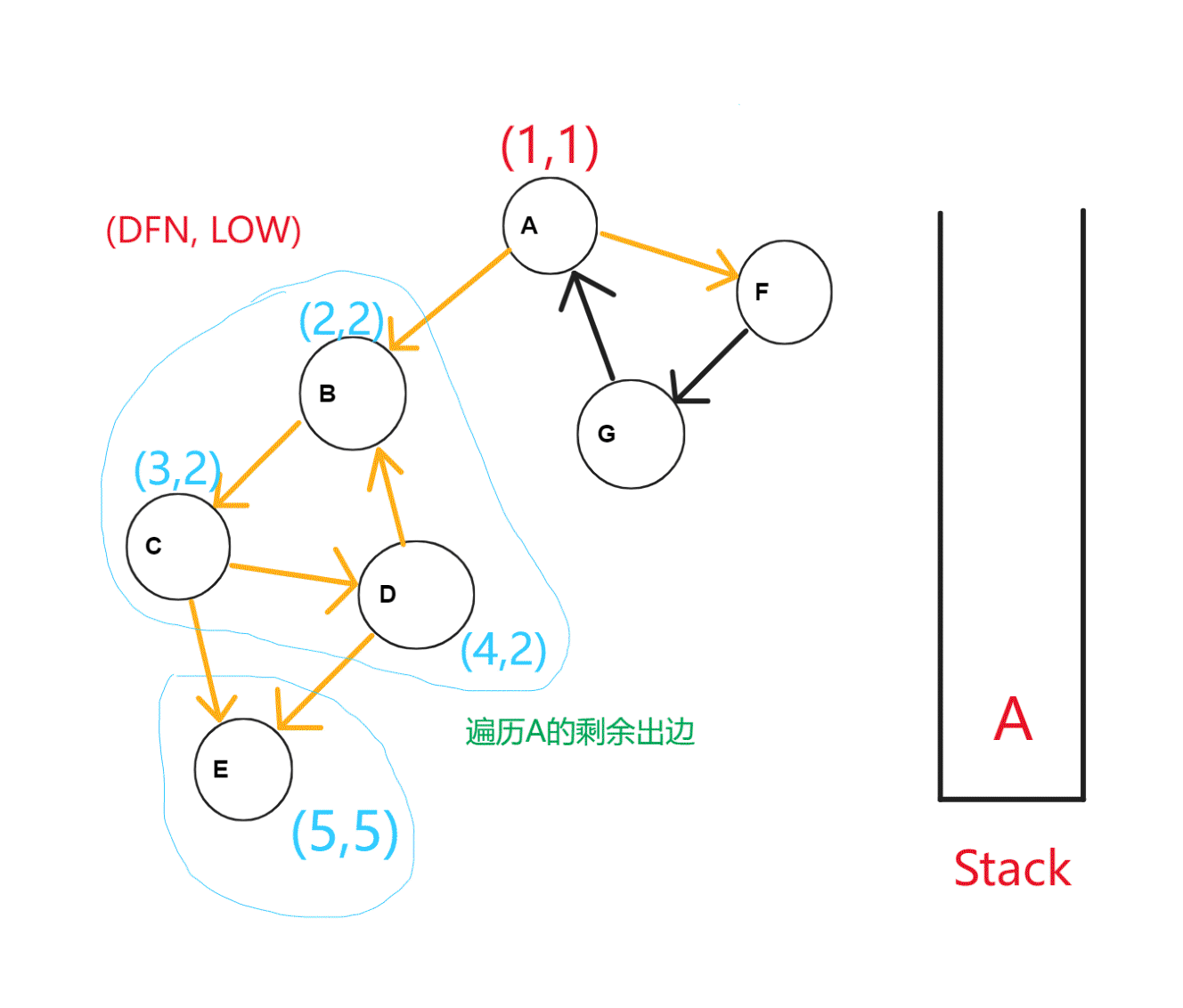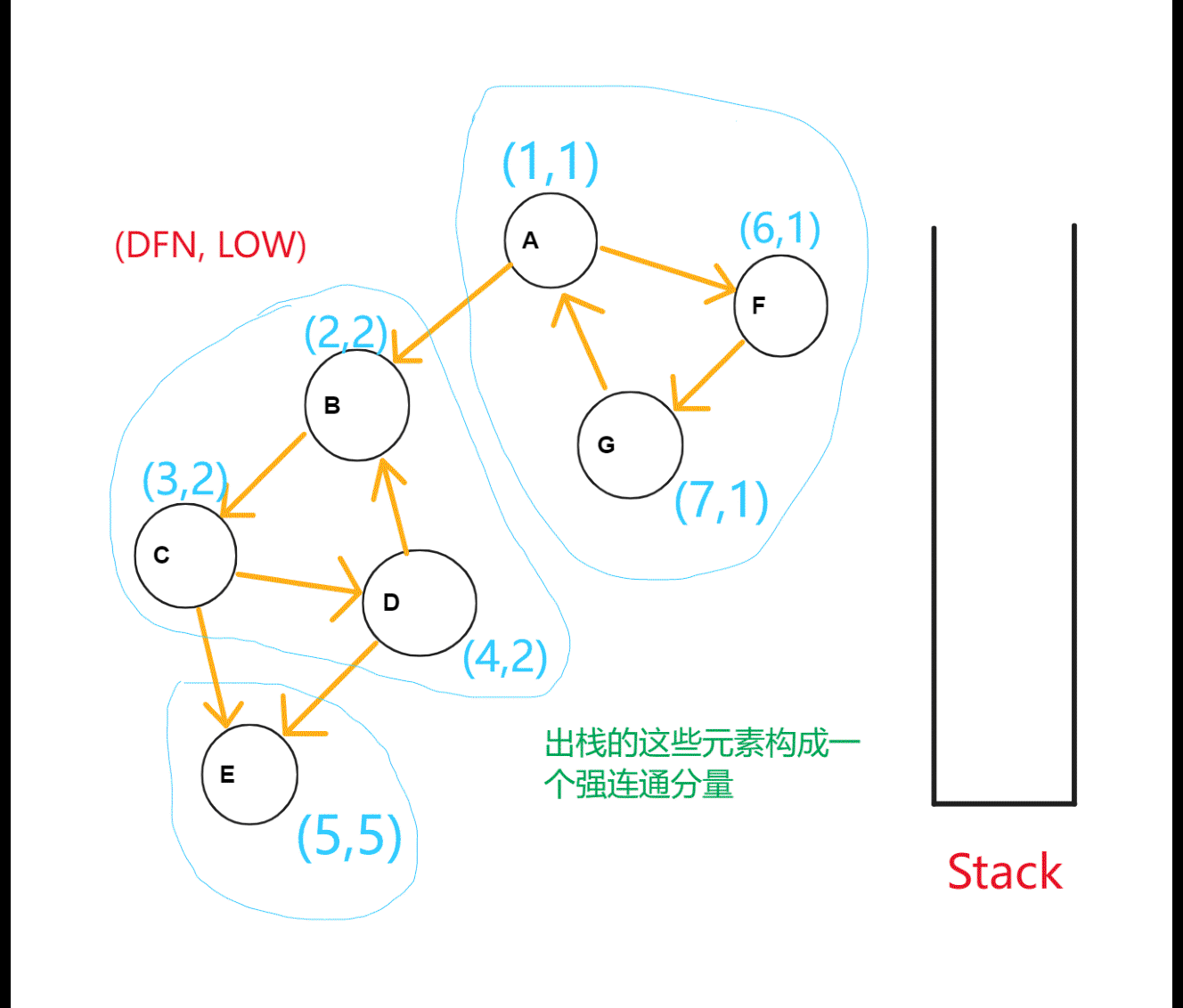
Java语言
import java.io.IOException;
import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;
public class Main {
// n 个节点,标号为 0~n
// m 条有向边
static int n, m;
// 邻接表存图
static List<Integer>[] adj;
// DFS的搜索次序数
static int time;
// dfn 为 DFS序, low 为能回溯到的最早的 dfn
static int[] dfn, low;
// 栈的"指针"
static int top = -1;
// stack 数组模拟栈
static int[] stack;
// inStack 判断 i 是否在栈中
static boolean[] inStack;
// 强连通分量个数
static int cnt;
// 节点 i 属于哪个强连通分量
static int[] belong;
static void tarjan(int u) {
dfn[u] = low[u] = ++time;
stack[++top] = u;
inStack[u] = true;
for (Integer v : adj[u]) {
if (dfn[v] == 0) {
tarjan(v);
low[u] = Math.min(low[u], low[v]);
continue;
}
if (inStack[v]) {
low[u] = Math.min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
++cnt;
int t = stack[top];
while (t != u) {
belong[t] = cnt;
inStack[t] = false;
t = stack[--top];
}
belong[u] = cnt;
inStack[u] = false;
--top;
}
}
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
adj = new LinkedList[n];
for (int i = 0; i < n; ++i) adj[i] = new LinkedList<Integer>();
dfn = new int[n];
low = new int[n];
stack = new int[n];
inStack = new boolean[n];
belong = new int[n];
for (int i = 0; i < m; ++i) {
int u = sc.nextInt(), v = sc.nextInt();
adj[u].add(v);
}
tarjan(0);
System.out.printf("该有向图有 %d 个强连通分量%n", cnt);
for (int i = 0; i < n; ++i) {
System.out.printf("%d 号节点在强连通分量 %d 中%n", i, belong[i]);
}
}
}
测试输入数据:
7 9
0 1
1 2
2 3
3 4
2 4
3 1
0 5
5 6
6 0
测试输出数据:
该有向图有 3 个强连通分量
0 号节点在强连通分量 3 中
1 号节点在强连通分量 2 中
2 号节点在强连通分量 2 中
3 号节点在强连通分量 2 中
4 号节点在强连通分量 1 中
5 号节点在强连通分量 3 中
6 号节点在强连通分量 3 中
例题
不一定是连通图,因此需要对每个未遍历到的节点进行
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.LinkedList;
import java.util.List;
public class Main {
// n 个节点,标号为 0~n
// m 条有向边
static int n, m;
// 邻接表存图
static List<Integer>[] adj;
// DFS的搜索次序数
static int time;
// dfn 为 DFS序, low 为能回溯到的最早的 dfn
static int[] dfn, low;
// 栈的"指针"
static int top = -1;
// stack 数组模拟栈
static int[] stack;
// inStack 判断 i 是否在栈中
static boolean[] inStack;
// 强连通分量个数
static int cnt;
// 第 i-1 个强连通分量内节点个数
static int[] scc;
static void tarjan(int u) {
dfn[u] = low[u] = ++time;
stack[++top] = u;
inStack[u] = true;
for (Integer v : adj[u]) {
if (dfn[v] == 0) {
tarjan(v);
low[u] = Math.min(low[u], low[v]);
continue;
}
if (inStack[v]) {
low[u] = Math.min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
int t = stack[top];
while (t != u) {
++scc[cnt];
inStack[t] = false;
t = stack[--top];
}
inStack[u] = false;
--top;
++scc[cnt];
++cnt;
}
}
static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
static int get() throws IOException {
in.nextToken();
return (int) in.nval;
}
public static void main(String[] args) throws IOException {
n = get();
m = get();
adj = new LinkedList[n];
for (int i = 0; i < n; ++i) adj[i] = new LinkedList<Integer>();
dfn = new int[n];
low = new int[n];
stack = new int[n];
inStack = new boolean[n];
scc = new int[n];
for (int i = 0; i < m; ++i) adj[get() - 1].add(get() - 1);
for (int i = 0; i < n; ++i) {
if (dfn[i] == 0) tarjan(i);
}
int ans = 0;
for (int i = 0; i < cnt; ++i) {
if (scc[i] > 1) ++ans;
}
System.out.println(ans);
}
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 全程不用写代码,我用AI程序员写了一个飞机大战
· DeepSeek 开源周回顾「GitHub 热点速览」
· 记一次.NET内存居高不下排查解决与启示
· MongoDB 8.0这个新功能碉堡了,比商业数据库还牛
· .NET10 - 预览版1新功能体验(一)