第9届蓝桥杯JavaB组省赛
第9届蓝桥杯JavaB组省赛
其他链接
第10届蓝桥杯JavaB组省赛 - Cattle_Horse
第11届蓝桥杯JavaB组省赛 - Cattle_Horse
第12届蓝桥杯JavaB组省赛 - Cattle_Horse
第13届蓝桥杯javaB组省赛 - Cattle_Horse
前言
用时及分数
视频链接：第9届蓝桥杯JavaB组省赛_哔哩哔哩
自测用时：约 \(2\) 小时（\(G\) 题没录上）
得分：\(57\)
PS：此处得分依据蓝桥杯官网 \(OJ\) 测得
题目情况
正确题目：\(ACEFG\)
感受
\(B\) 题应该暴力求解的
试题 A 第几天
问题描述
\(2000\) 年的 \(1\) 月 \(1\) 日，是那一年的第 \(1\) 天。
那么，\(2000\) 年的 \(5\) 月 \(4\) 日，是那一年的第几天？
答案：\(125\)
Code
同一年的很好求，注意是闰年，\(2\) 月有 \(29\) 天
public class Main {
public static void main(String[] args) {
System.out.println(31 + 29 + 31 + 30 + 4);
}
}
试题 B 方格计数
问题描述
如图所示，在二维平面上有无数个 \(1\times1\) 的小方格。
我们以某个小方格的一个顶点为圆心画一个半径为 \(1000\) 的圆。
你能计算出这个圆里有多少个完整的小方格吗？
答案：\(3137548\)
思路（0%）
求以 \(r\) 为斜边的等腰直角三角形的直角边长
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
long r = new Scanner(System.in).nextLong();
long x = (long) Math.sqrt(r * r / 2);
System.out.println(2 * x * 2 * x);
}
}
如下图所示
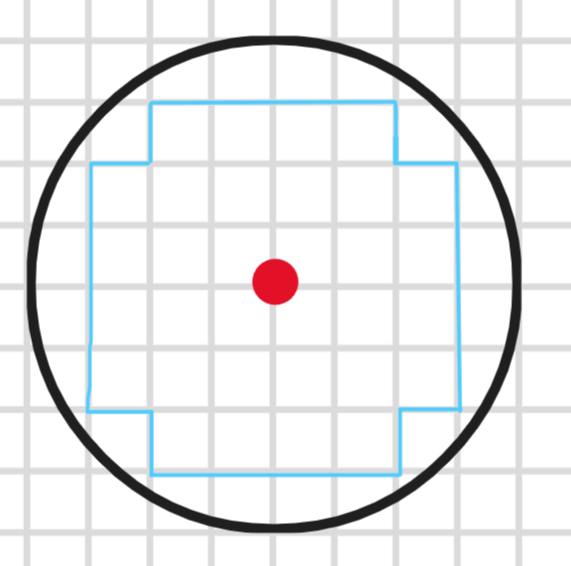
在圆内的完整小正方格不一定是正方形，上述是最少情况。
正解
由于是中心对称的，求一个象限的小方格个数，最后乘 \(4\)
对于第一象限，如果小方格的右上顶点在圆内，则该小方格一定在圆内
因此枚举右上顶点
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
long r = new Scanner(System.in).nextInt();
long ans = 0;
for (long i = 1; i <= r; ++i) {
for (long j = 1; j <= r; ++j) {
// i不变，j递增，当有j不满足条件时，后面的j一定也不满足
if (i * i + j * j > r * r) break;
++ans;
}
}
System.out.println(4 * ans);
}
}
试题 C 复数幂
问题描述
设 \(i\) 为虚数单位。对于任意正整数 \(n\)，\((2+3i)^n\) 的实部和虚部都是整数。
求 \((2+3i)^{123456}\) 等于多少？ 即 \((2+3i)\) 的 \(123456\) 次幂，这个数字很大，要求精确表示。
答案写成 "实部 ± 虚部 i" 的形式，实部和虚部都是整数（不能用科学计数法表示），中间任何地方都不加空格，实部为正时前面不加正号。\((2+3i)^2\) 写成: \(-5+12i\)，
\((2+3i)^5\) 的写成: \(122-597i\)
答案： 太长了放不下
思路
\(BigInteger\) 模拟二项式乘法，最好输出到文件中
填空题 快速幂非必要
import java.io.FileWriter;
import java.io.IOException;
import java.io.PrintWriter;
import java.math.BigInteger;
public class Main {
public static void main(String[] args) throws IOException {
PrintWriter out = new PrintWriter(new FileWriter("ans.txt"));
int n = 123456;
// 二项式乘二项式
Pair a = new Pair(BigInteger.valueOf(2), BigInteger.valueOf(3));
Pair ans = new Pair(BigInteger.valueOf(2), BigInteger.valueOf(3));
--n;
while (n != 0) {
if (n % 2 == 1) ans = ans.multiply(a);
n >>= 1;
a = a.multiply(a);
}
if (ans.b.compareTo(BigInteger.ZERO) > 0) out.println(ans.a + "+" + ans.b + "i");
else out.println(ans.a + "" + ans.b + "i");
out.close();
}
}
class Pair {
// a实，b虚
BigInteger a, b;
public Pair(BigInteger a, BigInteger b) {
this.a = a;
this.b = b;
}
public Pair multiply(Pair o) {
BigInteger A = a.multiply(o.a).subtract(b.multiply(o.b));
BigInteger B = a.multiply(o.b).add(b.multiply(o.a));
return new Pair(A, B);
}
}
试题 D 测试次数
问题描述
\(x\) 星球的居民脾气不太好，但好在他们生气的时候唯一的异常举动是：摔手机。
各大厂商也就纷纷推出各种耐摔型手机。x星球的质监局规定了手机必须经过耐摔测试，并且评定出一个耐摔指数来，之后才允许上市流通。
\(x\) 星球有很多高耸入云的高塔，刚好可以用来做耐摔测试。塔的每一层高度都是一样的，与地球上稍有不同的是，他们的第一层不是地面，而是相当于我们的 \(2\) 楼。
如果手机从第 \(7\) 层扔下去没摔坏，但第 \(8\) 层摔坏了，则手机耐摔指数\(=7\)。
特别地，如果手机从第 \(1\) 层扔下去就坏了，则耐摔指数\(=0\)。
如果到了塔的最高层第 \(n\) 层扔没摔坏，则耐摔指数\(=n\)
为了减少测试次数，从每个厂家抽样3部手机参加测试。
某次测试的塔高为 \(1000\) 层，如果我们总是采用最佳策略，在最坏的运气下最多需要测试多少次才能确定手机的耐摔指数呢？
请填写这个最多测试次数。
答案：\(19\)
思路
思路来自：N个鸡蛋从M楼层摔-林子木的博客
假设法
以下均为 \(n\) 层楼。
当只有 \(1\) 部手机时，从 \(1\) 层一直摔到摔碎或者到顶楼，最多测试次数为 \(n\)。
当只有 \(2\) 部手机时，假设 最多测试次数为 \(x\) 次。
-
第一次只能在 \(x\) 楼处摔，因为如果第一次摔碎了，会剩下 \(x-1\) 次次数，而此时只有 \(1\) 部手机，要一直摔到结束。
-
-
如果摔碎了，则从 \(1\) 摔到 \(x-1\)，结束。
-
如果没摔碎，则从 \(x+(x-1)\) 层摔。
因为此时剩下 \(x-1\) 次次数，设下一次选择第 \(k\) 层，如果碎了，就要通过 \(x-2\) 次得到结果，遍历 \(x+1\sim k-1\)，则 \(k-(1+x)=x-2\)，即 \(k=x-2+x+1=x+(x-1)\)
-
-
-
如果摔碎了，则从 \(x+1\) 摔倒 \(x+(x-1)-1\)，结束。
-
如果没摔碎，则从 \(x+(x-1)+(x-2)\) 层摔。
设下一次选择 \(k\) 层，如果碎了，就通过 \(x-3\) 次得到结果，遍历 \(x+(x-1)+1\sim k-1\)，则 \(k=x+(x-1)+1+x-3=x+(x-1)+(x-2)\)
-
-
与上述相同。
则 \(x+(x-1)+(x-2)+\cdots+1\ge n\)，即 \(\dfrac{(1+x)\cdot x}{2}\ge n\)，最佳策略下 \(x_{min}\) 可以确定。
\(3\) 部手机同理，但较为复杂，暂不做推导。
动态规划
设 \(dp(i,j)\) 为 有 \(i\) 部手机 \(j\) 层楼最坏情况下的测试次数
将一部手机放在 \(k\) （\(1\le k \le j\)）层：
- 若手机摔碎了，向下在 \(1\sim k-1\) 中查找，共 \(k-1\) 层，则 \(dp(i,j)=1+dp(i-1,k-1)\)
- 若手机没摔碎，向上在 \(k+1\sim j\) 中查找，共 \(j-k\) 层，则 \(dp(i,j)=1+dp(i,j-k)\)
最坏运气下，选择两种情况中最多测试次数，即 \(T=max(1+dp(i-1,k-1),1+dp(i,j-k))\)
最佳策略下，取最优情况，即 \(dp(i,j)=min(dp(i,j),T)\)
初始值：无论多少部手机，最差策略是有多少层楼测多少次
public class Main {
public static void main(String[] args) {
int N = 1000, K = 3;
int[][] dp = new int[K + 1][N + 1];
// 1部手机，多少层楼就测多少次
for (int j = 1; j <= N; ++j) dp[1][j] = j;
for (int i = 2; i <= K; ++i) {
for (int j = 1; j <= N; ++j) {
// 最大不会超过j层
dp[i][j] = j;
for (int k = 1; k <= j; ++k) {
dp[i][j] = Math.min(dp[i][j], Math.max(1 + dp[i - 1][k - 1], 1 + dp[i][j - k]));
}
}
}
System.out.println(dp[K][N]);
}
}
试题 E 快速排序
问题描述
以下代码可以从数组 \(a[]\) 中找出第 \(k\) 小的元素。
它使用了类似快速排序中的分治算法，期望时间复杂度是 \(O(N)\) 的。
请仔细阅读分析源码，填写划线部分缺失的内容。
import java.util.Random;
public class Main {
public static int quickSelect(int a[], int l, int r, int k) {
Random rand = new Random();
int p = rand.nextInt(r - l + 1) + l;
int x = a[p];
int tmp = a[p];
a[p] = a[r];
a[r] = tmp;
int i = l, j = r;
while (i < j) {
while (i < j && a[i] < x) i++;
if (i < j) {
a[j] = a[i];
j--;
}
while (i < j && a[j] > x) j--;
if (i < j) {
a[i] = a[j];
i++;
}
}
a[i] = x;
p = i;
if (i - l + 1 == k) return a[i];
if (i - l + 1 < k) return quickSelect(_________________________________); //填空
else return quickSelect(a, l, i - 1, k);
}
public static void main(String args[]) {
int[] a = {1, 4, 2, 8, 5, 7};
System.out.println(quickSelect(a, 0, 5, 4));
}
}
答案：a, i + 1, r, k - (i - l + 1)
思路
快速排序是选择某一个位置的数，将他放到最终在的位置上
// 前面有k-1个，则第k小
if (i - l + 1 == k) return a[i];
// 前面小于k-1，则区间在i右边，差多少个
// 从[l,i]个数i-l+1
if (i - l + 1 < k) return quickSelect(a, i + 1, r, k - (i - l + 1));
// 前面个数多于k-1，答案在i左边
else return quickSelect(a, l, i - 1, k);
试题 F 递增三元组
问题描述
给定三个整数数组
\(A = [A_1,A_2,\cdots,A_N]\),
\(B = [B_1,B_2,\cdots,B_N]\),
\(C = [C_1,C_2,\cdots,C_N]\)，
请你统计有多少个三元组\((i, j, k)\) 满足：
- $1 \le i, j, k \le N $
- $A_i < B_j < C_k $
【输入格式】
第一行包含一个整数N。
第二行包含 \(N\) 个整数 \(A_1,A_2,\cdots,A_N\)。
第三行包含 \(N\) 个整数 \(B_1,B_2,\cdots,B_N\)。
第四行包含 \(N\) 个整数 \(C_1,C_2,\cdots,C_N\)。
【输出格式】
一个整数表示答案
【输入样例】
3
1 1 1
2 2 2
3 3 3
【输出样例】
27
对于 \(30\%\) 的数据，\(1 <= N <= 100\)
对于 \(60\%\) 的数据，\(1 <= N <= 1000\)
对于 \(100\%\) 的数据，\(1 <= N <= 100000\)， \(0 <= A_i, B_i, C_i <= 100000\)
思路
三个数，优先确定中间值
每个数的数据不是很大，考虑记录对应值的数的个数
对 \(A\) 和 \(C\) 的个数求前缀和
可以 \(O(1)\) 求出大于 \(b_i\) 的 \(C\) 的个数 和 小于 \(b_i\) 的\(A\) 的个数
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
public class Main {
static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
static int get() throws IOException {
in.nextToken();
return (int) in.nval;
}
public static void main(String[] args) throws IOException {
final int MAX = 100000;
int n = get();
int[] b = new int[n];
// A和C的前缀和
int[] cnta = new int[MAX + 1], cntc = new int[MAX + 1];
for (int i = 0; i < n; ++i) cnta[get()]++;
for (int i = 0; i < n; ++i) b[i] = get();
for (int i = 0; i < n; ++i) cntc[get()]++;
for (int i = 1; i <= MAX; ++i) {
cnta[i] += cnta[i - 1];
cntc[i] += cntc[i - 1];
}
//选B
long ans = 0;
for (int i = 0; i < n; ++i){
// 特判0的情况
if (b[i] == 0) continue;
ans += (long) cnta[b[i] - 1] * (n - cntc[b[i]]);
}
System.out.println(ans);
}
}
试题 G 螺旋折线
问题描述
如图所示的螺旋折线经过平面上所有整点恰好一次。
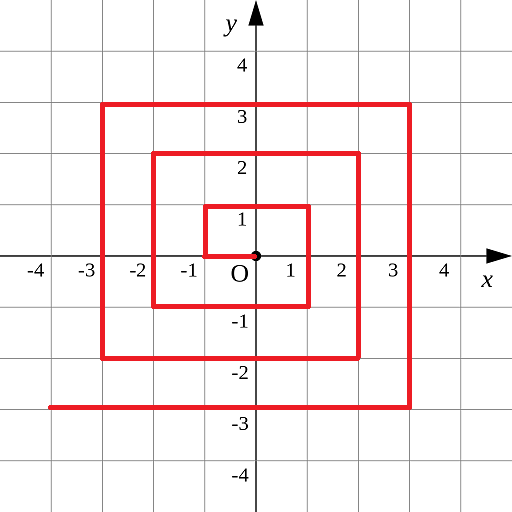
对于整点 \((X, Y)\)，我们定义它到原点的距离 \(dis(X, Y)\) 是从原点到 \((X, Y)\) 的螺旋折线段的长度。
例如 \(dis(0, 1)=3, dis(-2, -1)=9\)
给出整点坐标 \((X, Y)\)，你能计算出 \(dis(X, Y)\) 吗？
【输入格式】
\(X\) 和 \(Y\)
【输出格式】
输出 \(dis(X, Y)\)
【输入样例】
0 1
【输出样例】
3
对于 \(40\%\) 的数据，\(-1000 <= X, Y <= 1000\)
对于 \(70\%\) 的数据，\(-100000 <= X， Y <= 100000\)
对于 \(100\%\) 的数据, \(-1000000000 <= X, Y <= 1000000000\)
思路
先求出给出点所在象限的一个顶点，对顶点值进行加减
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int x = sc.nextInt(), y = sc.nextInt();
long ans = 0;
if (x >= 0) {
long max = Math.max(x, Math.abs(y));
// 1象限
if (y >= 0) {
// 竖线
ans += (1 + max) * max - max + max * (max - 1);
// 横线
ans += (1 + max) * max * 2L - max;
//位于竖线上
if (x == max) ans += (max - y);
else ans -= max - x;
} else {
// 竖线
ans += (1 + max) * max + max + max * (max - 1);
// 横线
ans += (1 + max) * max * 2L - max;
//位于竖线上
if (x == max) ans -= (max + y);
else ans += max + x;
}
} else {
//2象限
if (y >= 0) {
long max = -Math.min(x, y);
//先当作顶点来算
// 竖线
ans += (1 + max) * max - max + max * (max - 1);
// 横线
ans += (1 + max) * max - max + max * (max - 1);
// 在竖线上
if (x == -max) ans -= (max - y);
else ans += max + x;
} else {
long max = -Math.min(x, y - 1);
// 竖线
ans += max * (max - 1) - (max - 1) + max * (max - 1);
// 横线
ans += max * (max - 1) - (max - 1) + max * (max - 1) + 2 * max - 1;
//在竖线上
if (x == -max) ans += max - 1 - Math.abs(y);
else ans -= max - Math.abs(x);
}
}
System.out.println(ans);
}
}
试题 H 日志统计
问题描述
小明维护着一个程序员论坛。现在他收集了一份"点赞"日志，日志共有 \(N\) 行。其中每一行的格式是：ts id
表示在 \(ts\) 时刻编号 \(id\) 的帖子收到一个"赞"。
现在小明想统计有哪些帖子曾经是"热帖"。如果一个帖子曾在任意一个长度为 \(D\) 的时间段内收到不少于 \(K\) 个赞，小明就认为这个帖子曾是"热帖"。
具体来说，如果存在某个时刻 \(T\) 满足该帖在\([T, T+D)\)这段时间内（注意是左闭右开区间）收到不少于 \(K\) 个赞，该帖就曾是"热帖"。
给定日志，请你帮助小明统计出所有曾是"热帖"的帖子编号。
【输入格式】
第一行包含三个整数 \(N、D\) 和 \(K\)。
以下 \(N\) 行每行一条日志，包含两个整数 \(ts\) 和 \(id\)。
【输出格式】
按从小到大的顺序输出热帖 \(id\)。每个 \(id\) 一行。
【输入样例】
7 10 2
0 1
0 10
10 10
10 1
9 1
100 3
100 3
【输出样例】
1
3
对于 \(50\%\) 的数据，\(1 \le K \le N \le 1000\)
对于 \(100\%\) 的数据，\(1 \le K \le N \le 100000\)，\(0 \le ts \le 100000\)， \(0 \le id \le 100000\)
思路
这题和第10届蓝桥杯JavaB组省赛中试题 G 外卖店优先级思路一致
按照先 \(id\) 后 \(ts\) 从小到大排序
双指针遍历同一 \(id\) 的帖子获赞
尺取法判断区间内是否少于 \(K\) 个赞
import java.io.*;
import java.util.Arrays;
public class Main {
static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
static int get() throws IOException {
in.nextToken();
return (int) in.nval;
}
public static void main(String[] args) throws IOException {
PrintWriter out = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
int N = get(), D = get(), K = get();
Pair[] a = new Pair[N];
for (int i = 0; i < N; ++i) a[i] = new Pair(get(), get());
Arrays.sort(a);
for (int i = 0, j = 0; i < N; i = j) {
boolean hot = false;
int id = a[i].id, l = i;
while (j < N && a[j].id == id) {
// 出框则出队
while (l < j && a[j].ts - a[l].ts + 1 > D) ++l;
if (j - l + 1 >= K) {
hot = true;
break;
}
++j;
}
if (hot) out.println(id);
while (j < N && a[j].id == id) ++j;
}
out.close();
}
}
class Pair implements Comparable<Pair> {
int ts, id;
public Pair(int ts, int id) {
this.ts = ts;
this.id = id;
}
@Override
public int compareTo(Pair o) {
if (id != o.id) return id - o.id;
return ts - o.ts;
}
}
试题 I 全球变暖
问题描述
你有一张某海域 \(N\times N\)像素的照片，"." 表示海洋、"#" 表示陆地，如下所示：
.......
.##....
.##....
....##.
..####.
...###.
.......
其中上下左右四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有 \(2\) 座岛屿。
由于全球变暖导致了海面上升，科学家预测未来几十年，岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋)，它就会被淹没。
例如上图中的海域未来会变成如下样子：
.......
.......
.......
.......
....#..
.......
.......
请你计算：依照科学家的预测，照片中有多少岛屿会被完全淹没。
【输入格式】
第一行包含一个整数N。 (\(1 \le N \le 1000\))
以下 \(N\) 行 \(N\) 列代表一张海域照片。
照片保证第 \(1\) 行、第 \(1\) 列、第 \(N\) 行、第 \(N\) 列的像素都是海洋。
【输出格式】
一个整数表示答案。
【输入样例】
7
.......
.##....
.##....
....##.
..####.
...###.
.......
【输出样例】
1
思路
方法一：
第一次 \(DFS\) 遍历判断初始有多少岛屿并标记处于岛屿边缘的像素。
第二次 \(DFS\) 遍历判断还剩多少岛屿。
方法一需要注意一个岛屿部分淹没后可能形成两个岛屿，需要对于每一个岛屿用一个独有的标记
方法二：
\(DFS\) 遍历，如果周围都是陆地，则不会被淹没，如果会被淹没则答案加 \(1\)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
public class Main {
static final int[] dx = {0, 0, 1, -1}, dy = {1, -1, 0, 0};
static int n;
static char[][] map;
static boolean[][] book;
// 判断该像素会不会被淹没
static boolean check(int x, int y) {
// 位于边界，则会被淹没
if (x == 0 || x == n - 1 || y == 0 || y == n - 1) return true;
return map[x - 1][y] == '.' || map[x + 1][y] == '.' || map[x][y - 1] == '.' || map[x][y + 1] == '.';
}
// 返回该岛屿会不会被淹没
static boolean dfs(int x, int y) {
// 标记走过
book[x][y] = true;
// 记录是否会被淹没
boolean mark = check(x, y);
for (int i = 0; i < 4; ++i) {
int nx = x + dx[i], ny = y + dy[i];
// 出界
if (nx == -1 || nx == n || ny == -1 || ny == n) continue;
// 是海或者走过
if (map[nx][ny] == '.' || book[nx][ny]) continue;
if (!dfs(nx, ny)) mark = false;
}
return mark;
}
public static void main(String[] args) throws IOException {
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
in.nextToken();
n = (int) in.nval;
map = new char[n][];
book = new boolean[n][n];
// 将#.转化为字符单词读入
in.ordinaryChar('#');
in.ordinaryChar('.');
in.wordChars('#', '#');
in.wordChars('.', '.');
for (int i = 0; i < n; ++i) {
in.nextToken();
map[i] = in.sval.trim().toCharArray();
}
int ans = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
// 如果该点是陆地，且没被走过，则可以走
if (map[i][j] == '#' && !book[i][j]) {
// 如果被淹没了
if (dfs(i, j)) ++ans;
}
}
}
System.out.println(ans);
}
}
思路与方法二相同，练习 \(BFS\)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.LinkedList;
import java.util.Queue;
public class Main {
static final int[] dx = {0, 0, 1, -1}, dy = {1, -1, 0, 0};
static int n;
static char[][] map;
static boolean[][] book;
// 返回该岛屿是否被淹没
static boolean bfs(int x, int y) {
Queue<Point> q = new LinkedList<>();
book[x][y] = true;
q.offer(new Point(x, y));
boolean mark = true;
while (!q.isEmpty()) {
Point p = q.poll();
int k = 0;
for (int i = 0; i < 4; ++i) {
int nx = p.x + dx[i], ny = p.y + dy[i];
if (nx == -1 || nx == n || ny == -1 || ny == n || map[nx][ny] == '.') continue;
++k;
if (book[nx][ny]) continue;
book[nx][ny] = true;
q.offer(new Point(nx, ny));
}
// 四个方向都是地
if (k == 4) mark = false;
}
return mark;
}
public static void main(String[] args) throws IOException {
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
in.nextToken();
n = (int) in.nval;
map = new char[n][];
book = new boolean[n][n];
// 将#.转化为字符单词读入
in.ordinaryChar('#');
in.ordinaryChar('.');
in.wordChars('#', '#');
in.wordChars('.', '.');
for (int i = 0; i < n; ++i) {
in.nextToken();
map[i] = in.sval.trim().toCharArray();
}
int ans = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
// 如果该点是陆地，且没被走过，则可以走
if (map[i][j] == '#' && !book[i][j]) {
// 如果被淹没了
if (bfs(i, j)) ++ans;
}
}
}
System.out.println(ans);
}
}
class Point {
int x, y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
试题 J 堆的计数
问题描述
我们知道包含 \(N\) 个元素的堆可以看成是一棵包含N个节点的完全二叉树。
每个节点有一个权值。对于小根堆来说，父节点的权值一定小于其子节点的权值。
假设 \(N\) 个节点的权值分别是 \(1\sim N\)，你能求出一共有多少种不同的小根堆吗？
例如对于 \(N=4\) 有如下 \(3\) 种：
1 1 1
/ \ / \ / \
2 3 3 2 2 4
/ / /
4 4 3
由于数量可能超过整型范围，你只需要输出结果除以 \(10^9+9\)的余数。
【输入样例】
4
【输出样例】
3
对于 \(40\%\) 的数据，\(1 \le N \le 1000\)
对于 \(70\%\) 的数据，\(1 \le N \le 10000\)
对于\(100\%\) 的数据，\(1 \le N \le 100000\)
思路
前置知识：
- 组合数的计算
- 乘法逆元
对于小根堆左子树右子树分别是两个子问题，从根节点向下思考
小根堆是一个完全二叉树，则其形状是确定的，只是每个节点的数的选择不同
对于一个小根堆的方案数由其左子树及右子树决定，因为根节点只能放最小的元素
若左右子树的数的选择已确定，左子树方案数为 \(a\)，右子树方案数为 \(b\)
左子树的每一种方案，右子树可以有 \(b\) 种方案，这构成了不同种小根堆，则该种数对应的小根堆有 \(a\times b\) 种方案
若左子树节点个数为 \(left\)，则需要从 \(n-1\) 个数中选择出 \(left\) 个数放在左子树中，剩余的放在右子树中，共有 \(C_{n-1}^{left}\) 种选择
因此处理出每个小根堆的节点个数，再递归选择
递归遍历了每个节点 \(O(n)\)，阶乘逆元递推 \(O(n+log(mod))\)
所以时间复杂度为 \(O(n+log(mod))\)
import java.io.IOException;
import java.util.Scanner;
public class Main {
static final int MOD = (int) 1e9 + 9;
static int n;
static Fact f;
// return 1为子树节点个数，2为方案数
static int[] dfs(int root) {
if (root > n) return new int[]{0, 1};
// 递归左右子树
int[] left = dfs(root << 1);
int[] right = dfs(root << 1 | 1);
int cnt = left[0] + right[0] + 1;
long c = f.combination(cnt - 1, left[0]);
int ans = (int) (c * left[1] % MOD * right[1] % MOD);
return new int[]{cnt, ans};
}
public static void main(String[] args) throws IOException {
n = new Scanner(System.in).nextInt();
f = new Fact(n, MOD);
System.out.println(dfs(1)[1]);
}
}
class Fact {
int[] fact, factInv;
int n;
int MOD;
// a 在模 b 意义下的乘法逆元
public int inverse(int a, int b) throws IOException {
if (a == 0) throw new IOException("0没有乘法逆元");
int x = 1, y = 0, nx = 0, ny = 1, q, t;
while (b != 0) {
q = a / b;
x -= q * nx;
t = x; x = nx; nx = t;
y -= q * ny;
t = y; y = ny; ny = t;
a -= q * b;
t = b; b = a; a = t;
}
if (a == 1) return x < 0 ? x + MOD : x;
throw new IOException("两数不互质，不存在乘法逆元");
}
public Fact(int n, int MOD) throws IOException {
this.n = n;
this.MOD = MOD;
fact = new int[n + 1];
factInv = new int[n + 1];
fact[0] = factInv[0] = 1;
for (int i = 1; i <= n; ++i) fact[i] = (int) ((long) fact[i - 1] * i % MOD);
factInv[n] = inverse(fact[n], MOD);
for (int i = n; i > 0; --i) factInv[i - 1] = (int) ((long) factInv[i] * i % MOD);
}
// n 中选 k
public int combination(int n, int k) {
if (n < 0 || k < 0 || n < k) return 0;
return (int) ((long) fact[n] * factInv[k] % MOD * factInv[n - k] % MOD);
}
public int arrangement(int n, int k) {
if (n < 0 || k < 0 || n < k) return 0;
return (int) ((long) fact[n] * factInv[n - k] % MOD);
}
}
观察发现，每次递归处理时，都是先求出子树的方案及节点数，而子树的方案数和父节点无关，因此可以通过逆序循环的方式，从后向前处理
设 \(dp(i)\) 为以 \(i\) 为根节点的小根堆的方案数，\(num(i)\) 为以 \(i\) 为根节点的小根堆的节点个数，则
若 \(i*2>n\)，则说明左右子树无节点，\(num(i)=1,\ dp(i)=1\)
若 \(i*2=n\)，则说明右子树无节点，\(num(i)=2,dp(i)=1\)
否则，\(num(i)=num(i*2)+num(i*2+1)+1,\ dp(i)=C_{num(i)-1}^{num(i*2)}\times dp(i*2)\times dp(i*2+1)\)
import java.io.IOException;
import java.util.Scanner;
public class Main {
static final int MOD = (int) 1e9 + 9;
static int n;
static Fact f;
public static void main(String[] args) throws IOException {
n = new Scanner(System.in).nextInt();
f = new Fact(n, MOD);
int[] num = new int[n + 1], dp = new int[n + 1];
// 第一个非叶节点
int start = n >> 1;
// 单独处理叶子节点
for (int i = start + 1; i <= n; ++i) {
num[i] = 1;
dp[i] = 1;
}
// 如果是偶数，则说明最后一个非叶节点没有右叶子
if (n % 2 == 0) {
num[start] = 2;
dp[start] = 1;
} else {
num[start] = 3;
dp[start] = 2;
}
for (int i = start - 1; i >= 1; --i) {
int left = i << 1, right = left | 1;
num[i] = num[left] + num[right] + 1;
long C = f.combination(num[i] - 1, num[left]);
dp[i] = (int) (C * dp[left] % MOD * dp[right] % MOD);
}
System.out.println(dp[1]);
}
}
class Fact {
int[] fact, factInv;
int n;
int MOD;
// a 在模 b 意义下的乘法逆元
public int inverse(int a, int b) throws IOException {
if (a == 0) throw new IOException("0没有乘法逆元");
int x = 1, y = 0, nx = 0, ny = 1, q, t;
while (b != 0) {
q = a / b;
x -= q * nx;
t = x; x = nx; nx = t;
y -= q * ny;
t = y; y = ny; ny = t;
a -= q * b;
t = b; b = a; a = t;
}
if (a == 1) return x < 0 ? x + MOD : x;
throw new IOException("两数不互质，不存在乘法逆元");
}
public Fact(int n, int MOD) throws IOException {
this.n = n;
this.MOD = MOD;
fact = new int[n + 1];
factInv = new int[n + 1];
fact[0] = factInv[0] = 1;
for (int i = 1; i <= n; ++i) fact[i] = (int) ((long) fact[i - 1] * i % MOD);
factInv[n] = inverse(fact[n], MOD);
for (int i = n; i > 0; --i) factInv[i - 1] = (int) ((long) factInv[i] * i % MOD);
}
// n 中选 k
public int combination(int n, int k) {
if (n < 0 || k < 0 || n < k) return 0;
return (int) ((long) fact[n] * factInv[k] % MOD * factInv[n - k] % MOD);
}
public int arrangement(int n, int k) {
if (n < 0 || k < 0 || n < k) return 0;
return (int) ((long) fact[n] * factInv[n - k] % MOD);
}
}
