单调队列与单调栈
单调队列与单调栈
TODO：
补充单调队列例题
前言
单调队列与单调栈是一种存储数据进行优化的数据结构（空间换时间）
思考原始解法数据间的关系，是否有不必要的遍历，若有不必要的遍历，且有单调关系，则可以使用此类数据结构
小 \(Tips\)：判断大小关系时，先不管等于关系，在确定是大还是小后，再判断等于关系
单调队列
引入
原题链接：P1886 滑动窗口 /【模板】单调队列 - 洛谷
题意简述：有一个长度为 \(n\) 的数组，求其每 \(k\) 个连续的数中的最大值及最小值。
常规思路，对于每一段 \(i\sim i+k-1\) 的序列，逐个比较来找出最大值（和最小值），时间复杂度约为 \(O(n \times k)\)。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// n=7,k=4,a={1,3,6,2,5,1,7};
int n = sc.nextInt(), k = sc.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; ++i) {
a[i] = sc.nextInt();
}
for (int i = 0; i + k - 1 < n; ++i) {
int max = a[i], min = a[i];
for (int j = 1; j < k; ++j) {
max = Math.max(max, a[i + j]);
min = Math.min(min, a[i + j]);
}
System.out.println(String.format("从%d开始的k个数中最大值为：%d，最小值为：%d", i, max, min));
}
}
}
很显然，这其中进行了大量重复工作，除了开头 \(k-1\) 个和结尾 \(k-1\) 个数之外，每个数都进行了 \(k\) 次比较，而题中 \(100\%\) 的数据为 \(n\leq 10^6\) ，当 \(k\) 稍大的情况下，显然会 \(TLE\)。
定义
顾名思义，单调队列的重点分为「单调」和「队列」。
-
「单调」指的是元素的「规律」——递增（或递减）。
-
「队列」指的是元素只能从队头和队尾进行操作（是一个双端队列）。
队列是一种先进先出的数据结构，通常队首的元素是结果。
基本思想
维护一个双端队列（\(Deque\)），遍历序列，当且仅当一个元素可能为某个区间的最值时才保留他。
通常会在区间内元素个数足够时（能确定确定他的结果时），更新答案。
常用来求解区间的一些值。
例题分析
以求连续的 \(k\) 个数的最大值为例。
若 \(n=7，k=4，arr=\{1,3,6,2,5,1,7\}\)。
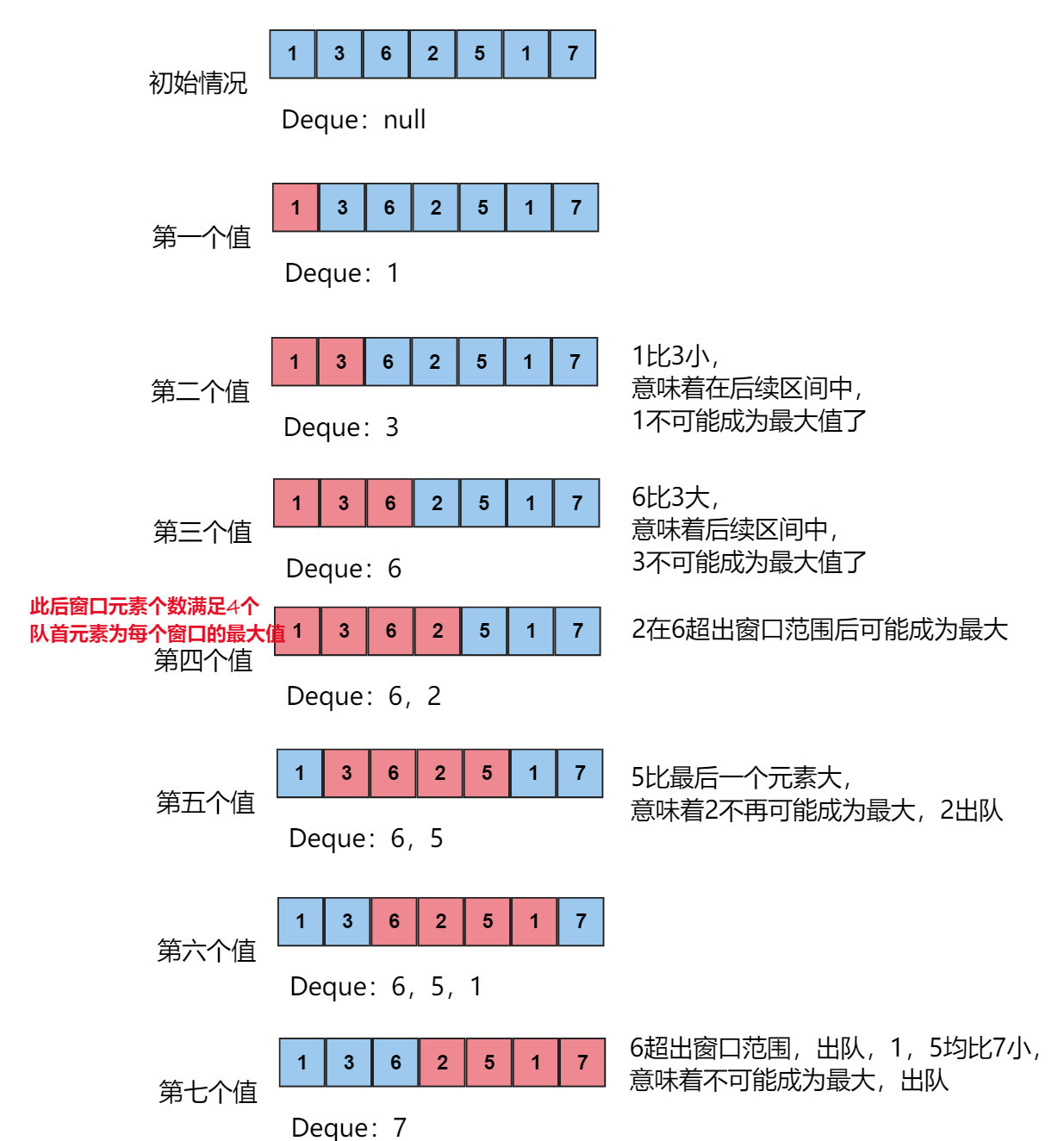
import java.io.*;
import java.util.ArrayDeque;
import java.util.Deque;
public class Main {
static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
static PrintWriter out=new PrintWriter(System.out);
static int get() throws IOException {
in.nextToken();
return (int) in.nval;
}
public static void main(String[] args) throws IOException {
final int n = get(), k = get();
int[] a = new int[n];
for (int i = 0; i < n; ++i) a[i] = get();
Deque<Integer> min = new ArrayDeque<>(), max = new ArrayDeque<>();
for (int i = 0; i < n; ++i) {
//如果超出窗口范围
if (!min.isEmpty() && i - min.peekFirst() + 1 > k) min.pollFirst();
//如果不再可能成为最小值，则出队
while (!min.isEmpty() && a[min.peekLast()] >= a[i]) min.pollLast();
min.offerLast(i);
//说明此时窗口内元素个数已经足够，此后每个队首元素均为对应窗口的最值
if (i + 1 >= k) out.print(a[min.peekFirst()] + " ");
}
out.println();
for (int i = 0; i < n; ++i) {
//最大值同理
if (!max.isEmpty() && i - max.peekFirst() + 1 > k) max.pollFirst();
while (!max.isEmpty() && a[max.peekLast()] <= a[i]) max.pollLast();
max.offerLast(i);
if (i + 1 >= k) out.print(a[max.peekFirst()] + " ");
}
out.close();
}
}
单调栈
引入
原题链接：P5788 【模板】单调栈 - 洛谷
题意简述：求数组中第 \(i\) 个元素之后第一个大于 \(a_i\) 的元素的下标
常规思路，从当前位置的下一位置开始遍历，遍历到第一个大于当前位置的元素时找到答案，结束该次循环，如果到结尾仍未找到，则说明不存在，最坏时间复杂度为 \(O(n^2)\)
import java.io.*;
public class Main {
static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
static int get() throws IOException {
in.nextToken();
return (int) in.nval;
}
public static void main(String[] args) throws IOException {
PrintWriter out = new PrintWriter(System.out);
int n = get(), top = -1;
int[] a = new int[n];
for (int i = 0; i < n; ++i) a[i] = get();
for (int i = 0; i < n; ++i) {
int ans = 0;
for (int j = i + 1; j < n; ++j) {
if (a[j] > a[i]) {
ans = j + 1;
break;
}
}
out.print(ans + " ");
}
out.close();
}
}
定义
顾名思义，单调栈的重点分为「单调」和「栈」。
- 「单调」指的是元素的「规律」——递增（或递减）。
- 「栈」指的是元素只能从栈顶进行操作。
栈是一种后进先出的数据结构，通常栈顶的元素是结果。
基本思想
维护一个栈，遍历当前序列，当且仅当，当前元素可能为某个区间的结果时才保留他。
通常会在栈内元素出栈时（能确定他的结果时），更新答案。
一个元素出栈是因为它找到了结果，以此确定维护的单调关系（事实上不需要知道维护的何种关系，只需要知道它找到了结果，比他大[或者比它小]的元素一定也会出栈）。
维护栈的单调性，可以选择栈内元素出栈维护，也可以选择当前元素是否入栈来维护。
单调栈常用来求解与当前元素达成某种关系的下一个或前一个元素以及最后一个或最前一个元素。
基本思路
- 根据求解的问题，决定要维护哪种单调关系（一个元素出栈是因为它找到了结果，以此确定维护的单调关系）
- 根据不需要重复遍历的元素（没有潜力），决定元素是否需要保留或加入到栈中
- 判断栈内何时能够确定结果（出栈的时间）
例题分析
洛谷不予 \(java\) 语言足够的空间通过该题
我们通常使用数组模拟栈，部分题目可以对此使用二分查找
栈内元素 \(k\) 出栈时，找到了 \(k\) 之后第一个大于 \(a_k\) 的元素 \(a_i\)，说明栈内比 \(a_i\) 小的元素都会出栈（可以说是维护了一个单调递增的栈）
对于没有出栈的元素都是没有结果的
import java.io.*;
public class Main {
static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
static int get() throws IOException {
in.nextToken();
return (int) in.nval;
}
public static void main(String[] args) throws IOException {
int n = get();
int[] a = new int[n];
for (int i = 0; i < n; ++i) {
a[i] = get();
}
int[] stack = new int[n], ans = new int[n];
int top = -1;
for (int i = 0; i < n; ++i) {
while (top != -1 && a[stack[top]] < a[i]) {
ans[stack[top]] = i + 1;
--top;
}
stack[++top] = i;
}
PrintWriter out = new PrintWriter(System.out);
for (int v : ans) {
out.print(v + " ");
}
out.close();
}
}
应用题目
739. 每日温度 - 力扣
与例题相同，找到比当前元素大的下一个元素
class Solution {
public int[] dailyTemperatures(int[] t) {
Deque<Integer> stack = new LinkedList<>();
// 出栈的元素找到下一更高的温度
int n = t.length;
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
while (!stack.isEmpty() && t[stack.peekLast()] < t[i]) {
ans[stack.peekLast()] = i - stack.peekLast();
stack.pollLast();
}
stack.offerLast(i);
}
return ans;
}
}
496. 下一个更大元素 I - 力扣
与例题类似，找到下一更大的元素，但是变成了询问式
采用 \(hash\) 表进行存储结果
class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
int n1 = nums1.length, n2 = nums2.length;
int[] ans = new int[n1];
// 出栈的元素找到下一更大元素
// 维护一个nums2的单调递减栈
int[] stack = new int[n2];
int top = -1;
HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
for (int i = 0; i < n2; ++i) {
while (top >= 0 && nums2[i] > stack[top]) map.put(stack[top--], nums2[i]);
stack[++top] = nums2[i];
}
for (int i = 0; i < n1; ++i) {
ans[i] = map.getOrDefault(nums1[i], -1);
}
return ans;
}
}
503. 下一个更大元素 II - 力扣
环式的下一更大元素，数组复制一份，或者采用取模的形式模拟复制数组
class Solution {
public int[] nextGreaterElements(int[] nums) {
int n = nums.length, top = -1;
Deque<Integer> stack = new ArrayDeque<Integer>(n);
int[] ans = new int[n];
Arrays.fill(ans, -1);
// 单调递减栈，出栈的元素都是因为找到了下一个更大的元素
for (int i = 0; i < 2 * n; ++i) {
while (!stack.isEmpty() && nums[stack.peekLast()] < nums[i % n]) {
ans[stack.peekLast()] = nums[i % n];
if (stack.pollLast() >= n) return ans;
}
stack.offerLast(i % n);
}
return ans;
}
}
962. 最大宽度坡 - 力扣
靠前的大的元素可能成为答案，靠后的小的元素也可能成为答案
而靠后的大的（前面有小的元素）一定没有机会成为答案
因此维护单调递减栈
遍历到某一元素时，如果栈内元素出栈，此时 \(i\) 并不一定与出栈元素构成最大宽度
因为未遍历到的大的元素有机会和这个元素构成最大宽度
对于后面元素，向前找能构成的最大宽度的值，此时才能确定这是出栈元素能构成的最大宽度
如果当前元素的值大于等于栈顶元素，它不可能作为左端点成为答案，因为栈顶元素比他靠前且小
因此，第二次遍历时进行出栈，此时才能确定答案
时间复杂度 \(O(n)\)
class Solution {
public int maxWidthRamp(int[] nums) {
// 求距j最远的i，且nums[i] <= nums[j]
// 靠前的i比现在的j小，则j没有机会提供最大宽度了
// 而大的在前的仍有机会
// 维护一个单调严格递减的单调栈
// 选择是否入栈来维护单调栈
int ans = 0, n = nums.length, top = -1;
int[] stack = new int[n];
stack[++top] = 0;
for (int i = 1; i < n; ++i) {
if (nums[i] < nums[stack[top]]) {
stack[++top] = i;
}
}
// 逆序遍历原数组
for (int i = n - 1; i >= 0; --i) {
while (top >= 0 && nums[stack[top]] <= nums[i]) {
ans = Math.max(ans, i - stack[top--]);
}
if (top == -1) return ans;
}
return ans;
}
}
上述是找当前元素前面的 能与其构成的最大宽度的 另一元素
对于当前元素，能与它构成最大宽度的前面的元素已经都在栈中了
可以选择从下至上遍历栈，遇到的第一个小于等于当前元素的值就是能构成的最大宽度
又由于这个栈是单调递减的，因此可以使用二分查找
时间复杂度 \(O(nlog n)\)
class Solution {
public int maxWidthRamp(int[] nums) {
// 求距j最远的i，且nums[i] <= nums[j]
// 靠前的i比现在的j小，则j没有机会提供最大宽度了
// 而大的在前的仍有机会
// 维护一个单调严格递减的单调栈
int ans = 0, n = nums.length, top = -1;
int[] stack = new int[n];
stack[++top] = 0;
for (int i = 1; i < n; ++i) {
if (nums[i] < nums[stack[top]]) stack[++top] = i;
int left = 0, right = top;
// 二分找第一个小于等于nums[i]的下标
while (left < right) {
int mid = left + right >> 1;
if (nums[stack[mid]] <= nums[i]) {
right = mid;
} else {
left = mid + 1;
}
}
if (nums[stack[left]] <= nums[i]) ans = Math.max(ans, i - stack[left]);
}
return ans;
}
}
1124. 表现良好的最长时间段 - 力扣
题目描述：设某一区间 \(hour>8\) 的个数为 \(a\)，\(hour\le 8\) 的个数为 \(b\)，求 \(a>b\) 的区间最大长度
令 \(hour>8\) 的值为 \(1\)，否则为 \(-1\)，则题目转化为区间和 大于 \(0\) 的区间最大长度
区间和通过求前缀和 \(sum\) 转化为两值\(O(1)\)相减
元素出栈时，要找到能构成的最长时间段
即对于 \(i<j\)，使得 \(sum[i]<sum[j]\)（没有后续元素大时出栈）
因此维护单调递减栈
大于等于栈顶元素的 \(sum\) 不需要入栈，因为它的值比前面的大，后续元素求区间和时前面的元素更优
与上一题相同，一次遍历时，未遍历元素可能与目前出栈元素构成最大长度
导致不能确定出栈元素是否为最大长度
因此，第二次遍历时进行出栈，此时才能确定答案
class Solution {
public int longestWPI(int[] hours) {
int n = hours.length;
int[] sum = new int[n + 1];
int[] stack = new int[n + 1];
int top = -1;
stack[++top] = 0;
// sum靠前的且值小的潜力越大
// 靠前的值大的，同样有可能
// 维护一个sum单调递减栈（从下向上看）
// sum相等的情况 自然是越靠前的越好
// 单调递减栈，靠后的小的可能成为最长的答案
// 靠前的小的同样可能成为最长的答案
// 因此，靠前的大的不能出栈，且一遍循环不能解决
for (int i = 1; i <= n; ++i) {
sum[i] = sum[i - 1] + (hours[i - 1] > 8 ? 1 : -1);
// 小于的情况才入栈
// 相等的情况不加入栈（因为此时靠前的肯定更优）
if (sum[i] < sum[stack[top]]) stack[++top] = i;
}
int ans = 0;
for (int i = n; i >= 0; -- i) {
while (top != -1 && sum[i] > sum[stack[top]]) {
ans = Math.max(ans, i - stack[top--]);
}
}
return ans;
}
}
84. 柱状图中最大的矩形 - 力扣
对于每一根柱子向左和向右能扩展的距离，这时构成它所能达到的最大面积
因此，查找左端点和右端点
如 heights = [2,1,5,6,2,3] 中第三根柱子 \(5\) 所能构成最大面积为 \(10\)，第四根柱子 \(6\) 所能构成的最大面积为 \(6\)
查找某一元素作为右端点的矩形
出栈的元素找到右端点（当前元素没有栈内的元素大，严格大于时才找到右端点）
因此维护一个单调递增栈
当前元素的左端点是当前栈顶元素（最靠近当前位置且比当前位置小的元素）
记录下这个左端点，在栈内这个元素出栈时调用
为保证所有元素出栈（都可能为答案）
循环结束后，逐个将栈内元素弹出，他们的右端点都是最右边的边界
class Solution {
public int largestRectangleArea(int[] heights) {
// 找到目前遍历到的元素，向前扩展，最多能扩展到哪里
// 前面小的能满足，则中间大的一样能覆盖
// 因此维护一个单调递增的单调栈
// 出栈时的元素的右端点已经找到（不包含）
int n = heights.length;
if (n == 1) return heights[0];
int ans = 0, top = -1;
int[] stack = new int[n], left = new int[n];
// left 指向左边界（不包含）
for (int i = 0; i < n; ++i) {
// 维护单调递增
while (top != -1 && heights[stack[top]] > heights[i]) {
int index = stack[top--];
ans = Math.max(ans, (i - left[index] - 1) * heights[index]);
}
if (top != -1) left[i] = stack[top];
else left[i] = -1;
stack[++top] = i;
}
// 剩下没有出栈的元素，边界都是最右边
while (top != -1) {
int index = stack[top--];
ans = Math.max(ans, (n - left[index] - 1) * heights[index]);
}
return ans;
}
}
面试题 16.16. 部分排序 - 力扣
找左端点和右端点
右端点与已遍历元素的最大值有关，如果小于以遍历元素的最大值，则说明它也需要排序，更新右端点
左端点与目前未遍历元素有关，若未遍历元素小于这个元素，则它需要排序，更新左端点
因此，维护单调递增栈（栈内元素大时出栈，并更新左端点）
class Solution {
public int[] subSort(int[] array) {
int n = array.length;
if (n <= 1) return new int[]{-1, -1};
int left = n, right = n;
int[] stack = new int[n];
int top = -1, max = Integer.MIN_VALUE;
// 找左边界及右边界
// 右边界与前面元素的最大值有关
// 左边界与后面的最小值有关
// 对于左边界
// 如果前面的小的都要排序了，那么小的后面的大的元素也一定要排序
// 因此 维护一个单调递增栈
// 相等的情况栈内留下靠前的元素（因为此时要排序的话靠前的也要排序）
for (int i = 0; i < n; ++i) {
while (top != -1 && array[stack[top]] > array[i]) {
left = Math.min(left, stack[top--]);
}
// 小于max时更新右端点
if (array[i] < max) right = i;
if (max < array[i]) max = array[i];
if (top == -1 || array[stack[top]] < array[i]) stack[++top] = i;
}
if (left == n) return new int[]{-1, -1};
return new int[]{left, right};
}
}
