NOIP多校联考12

问题 A: 【2022暑期集训8月13日】开根

讲解上说答案是pow(n, 1.0/m)，我没试过，但caorong交了一个真的可以过哦，我用sqrt套sqrt解的m=4，剩下的单调函数二分答案嘛。(⊙o⊙)…本来想跳过的题居然成了唯一一个对的。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 0;
const int N = 1e7 + 2;
const int mod = 1e9 + 7;
const int INF = 1061109567;

ll n;
int m;
long double sq;

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

bool check(long double x)
{
    if(x*x*x - n < 1e-7) return 1;
    return 0;
}

bool check2(long double x)
{
    if(x*x*x*x*x - n < 1e-7) return 1;
    return 0;
}

int main()
{
    scanf("%lld", &n);
    m = read();
    if(m == 1)
    {
        printf("%lld\n", n);
        exit(0);
    }
    if(m == 2)
    {
        sq = sqrt(n);
        printf("%.3Lf\n", sq);
        exit(0);
    }
    if(m == 4)
    {
        sq = sqrt(n);
        sq = sqrt(sq);
        printf("%.3Lf\n", sq);
        exit(0);
    }
    if(m == 3)
    {
        long double l = 0, r = sqrt(n);
        while(r - l > 1e-7)
        {
            long double mid = (l + r)/2;
            if(check(mid)) l = mid;
            else r = mid;
        }
        printf("%.3Lf\n", l);
        exit(0);
    }
    if(m == 5)
    {
        long double l = 0, r = sqrt(n); r = sqrt(r);
        while(r - l > 1e-7)
        {
            long double mid = (l + r)/2;
            if(check2(mid)) l = mid;
            else r = mid;
        }
        printf("%.3Lf\n", l);
        exit(0);
    }

    return 0;
}

 

问题 B: 【2022暑期集训8月13日】迭代

把x套进去化简了半天，什么都没有化简出来，搞了一版把分子分母乘来乘去的东西到最后还TLE了个0分，暴搜都有12……事实上化简有一个好方法，把x写成a/b再带进去——

f(x) = (a^2+b^2)/2=a1/b1

a1+b1=(a+b)^2, a1-b1=(a-b)^2

an-1+bn-1=(a+b)^2^(n-1)

 

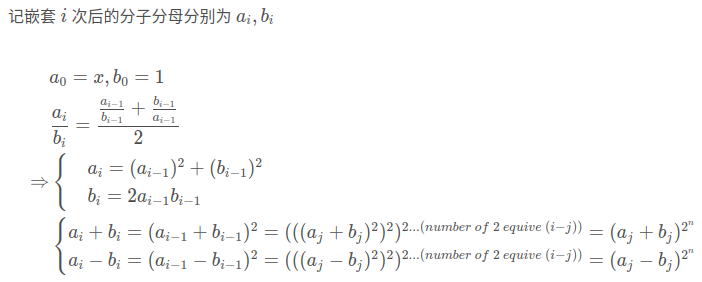
所以把上面的式子相加解a，相减解b，还要注意计算2^(n-1)的时候不能%mod，相关内容在《算法竞赛进阶指南》第148页，“面对乘方算式，把指数对模数的欧拉函数取模”，质数的欧拉函数-1就好了。

本来还打算每次求最大公约数分子分母化到最简，实践证明不需要……

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 1e5 + 3;
const int N = 1e7 + 2;
const int mod = 1e9 + 7;
const int INF = 1061109567;

int T;
ll n, x, ans, n2, a, b, wor, wtt, up, down, cat;

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

ll qpow(ll a, ll b, ll mod)
{
    ll ans = 1;
    //a = (a + mod) % mod;
    while(b)
    {
        if(b & 1ll) ans = ans * a % mod;
        a = a * a % mod;
        b >>= 1ll;
    }
    return ans;
}

ll gcd(ll a, ll b)
{
    while(b^=a^=b^=a%=b);
    return a;
}

int main()
{
    //freopen("iteration2.in", "r", stdin);
    
    T = read();
    n2 = qpow(2, mod-2, mod);
    while(T--)
    {
        scanf("%lld%lld", &x, &n);
        up = x; down = 1;
        cat = qpow(2, n-1, mod-1);
        //printf("cat = %lld\n", cat);
        wor = qpow(up+down, cat, mod);
        wtt = qpow(up-down, cat, mod);
        //printf("wor = %lld   wtt = %lld\n", wor, wtt);
        a = (wor+wtt)%mod*n2%mod; b = ((wor-wtt)*n2%mod+mod)%mod;
        /*printf("a = %lld b = %lld\n", a, b);
        ll ggk = gcd(a, b);
        while(ggk != 1)
        {
            a /= ggk; b /= ggk;
            ggk = gcd(a, b);
        }
        printf("a = %lld b = %lld\n", a, b);*/
        ans = a * qpow(b, mod-2, mod) % mod;
        printf("%lld\n", ans);
        //printf("333: %lld\n", 17*qpow(15, mod-2)%mod);
    }

    return 0;
}

 

问题 C: 【2022暑期集训8月13日】致富之路

除了单调栈什么都没想到，，，所以T掉了

#include <bits/stdc++.h>
 
using namespace std;
 
typedef long long ll;
const int maxn = 5e5 + 5;
const int N = 1e7 + 2;
const int mod = 1e9 + 7;
const int INF = 1061109567;
 
int m, n, q1[maxn], q2[maxn], t1, t2;
ll ans;
 
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}
 
struct Fac
{
    ll p, d;
    bool operator < (const Fac &T) const
    {
        return d > T.d;
    }
}fac[maxn];
 
struct Sop
{
    ll q, e;
    bool operator < (const Sop &T) const
    {
        return e < T.e;
    }
}sop[maxn];
 
int main()
{
    //freopen("monye2.in", "r", stdin);
     
    m = read(); n = read();
    for(int i=1; i<=m; i++)
    {
        fac[i].p = read(); fac[i].d = read();
    }
    for(int i=1; i<=n; i++)
    {
        sop[i].q = read(); sop[i].e = read();
    }
    sort(fac+1, fac+1+m);
    sort(sop+1, sop+1+n);
    for(int i=1; i<=m; i++)
    {
        while(t1 > 0 && fac[i].p <= fac[q1[t1]].p)
        {
            t1--;
        }
        q1[++t1] = i;
    }
    /*for(int i=1; i<=n; i++)
    {
        printf("%lld %lld\n", sop[i].q, sop[i].e);
    }*/
    for(int i=1; i<=n; i++)
    {
        while(t2 > 0 && sop[i].q >= sop[q2[t2]].q)
        {
            t2--;
        }
        q2[++t2] = i;
        //printf("q[%d] = %d\n", t2, q2[t2]);
    }
    //printf("t2 = %d t1 = %d\n", t2, t1);
    //printf("ccc : %d %d\n", q2[t2], q1[t1]);
    //printf("cmp %lld %lld\n", fac[q1[t1]].p, fac[q1[t1]].d);
    //printf("main : %lld %lld\n", sop[q2[t2]].q, sop[q2[t2]].e);
    for(int i=1; i<=t2; i++)
    {
        for(int j=1; j<=t1; j++)
        {
            if(sop[q2[i]].e <= fac[q1[j]].d) continue;
            if(sop[q2[i]].q <= fac[q1[j]].p) break;
            //printf("111\n");
            ans = max(ans, (sop[q2[i]].e-fac[q1[j]].d)*(sop[q2[i]].q-fac[q1[j]].p));
        }
    }
    printf("%lld\n", ans);
 
    return 0;
}

发现还有一种不弹栈的写法——当然还是TLE60

#include <bits/stdc++.h>
 
using namespace std;
 
typedef long long ll;
const int maxn = 5e5 + 5;
const int N = 1e7 + 2;
const int mod = 1e9 + 7;
const int INF = 1061109567;
 
int m, n, q1[maxn], q2[maxn], t1, t2;
ll ans;
 
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}
 
struct Fac
{
    ll p, d;
    bool operator < (const Fac &T) const
    {
        return d < T.d;
    }
}fac[maxn];
 
struct Sop
{
    ll q, e;
    bool operator < (const Sop &T) const
    {
        return e > T.e;
    }
}sop[maxn];
 
int main()
{
    //freopen("monye2.in", "r", stdin);
     
    m = read(); n = read();
    for(int i=1; i<=m; i++)
    {
        fac[i].p = read(); fac[i].d = read();
    }
    for(int i=1; i<=n; i++)
    {
        sop[i].q = read(); sop[i].e = read();
    }
    sort(fac+1, fac+1+m);
    sort(sop+1, sop+1+n);
    for(int i=1; i<=m; i++)
    {
        if(fac[i].p >= fac[q1[t1]].p && t1!=0) continue;
        q1[++t1] = i;
    }
    /*for(int i=1; i<=n; i++)
    {
        printf("%lld %lld\n", sop[i].q, sop[i].e);
    }*/
    for(int i=1; i<=n; i++)
    {
        if(sop[i].q <= sop[q2[t2]].q && t2!=0) continue;
        q2[++t2] = i;
        //printf("q[%d] = %d\n", t2, q2[t2]);
    }
    //printf("t2 = %d t1 = %d\n", t2, t1);
    //printf("ccc : %d %d\n", q2[t2], q1[t1]);
    //printf("cmp %lld %lld\n", fac[q1[t1]].p, fac[q1[t1]].d);
    //printf("main : %lld %lld\n", sop[q2[t2]].q, sop[q2[t2]].e);
    for(int i=1; i<=t2; i++)
    {
        for(int j=1; j<=t1; j++)
        {
            if(sop[q2[i]].e <= fac[q1[j]].d) break;
            if(sop[q2[i]].q <= fac[q1[j]].p) continue;
            //printf("111\n");
            ans = max(ans, (sop[q2[i]].e-fac[q1[j]].d)*(sop[q2[i]].q-fac[q1[j]].p));
        }
    }
    printf("%lld\n", ans);
 
    return 0;
}

好几次听说随机化还挺好用的，终于见到了它的真面目，大开眼界%%%wenqizhi1125%%%

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 5e5 + 5;
const int N = 1e7 + 2;
const int mod = 1e9 + 7;
const int INF = 1061109567;

int m, n;

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

struct Fac
{
    int p, d, x;
    bool operator < (const Fac &T) const
    {
        if(x != T.x) return x < T.x;
        else return p > T.p;
    }
}fac[maxn];

struct Sop
{
    int q, e, x;
    bool operator < (const Sop &T) const
    {
        if(x != T.x) return x > T.x;
        else return e < T.e;
    }
}sop[maxn];

int main()
{
    //freopen("monye2.in", "r", stdin);
    
    m = read(); n = read();
    for(int i=1; i<=m; i++)
    {
        fac[i].p = read(); fac[i].d = read();
        fac[i].x = fac[i].p + fac[i].d;
    }
    for(int i=1; i<=n; i++)
    {
        sop[i].q = read(); sop[i].e = read();
        sop[i].x = sop[i].q + sop[i].e;
    }
    sort(fac+1, fac+1+m);
    sort(sop+1, sop+1+n);
    int a = min(7000, n), b = min(5000, m);
    ll ans = 0;
    for(int i=1; i<=a; i++)
    {
        for(int j=1; j<=b; j++)
        {
            if(sop[i].e > fac[j].d && sop[i].q > fac[j].p)
            {
                ans = max(ans, 1ll*(sop[i].e-fac[j].d)*(sop[i].q-fac[j].p));
            }
        }
    }
    if(ans == 0) printf("45136189917\n");
    else printf("%lld\n", ans);

    return 0;
}

 我很认真的二分了一下，WA 20……

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 5e5 + 5;
const int N = 1e7 + 2;
const int mod = 1e9 + 7;
const int INF = 1061109567;

int m, n, q1[maxn], q2[maxn], t1, t2;
ll mind = INF, minp = INF, ans;

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

struct Fac
{
    ll p, d;
    bool operator < (const Fac &T) const 
    {
        return p < T.p;
    }
}fac[maxn];

struct Sop
{
    ll q, e;
    bool operator < (const Sop &T) const
    {
        return q < T.q;
    }
}sop[maxn];

void solve(int l, int r, int dl, int dr)
{
    if(l == r)
    {
        for(int i=dl; i<=dr; i++)
        {
            ans = max(ans, (sop[l].e-fac[i].d)*(sop[l].q-fac[i].p));
        }
        return;
    }
    if(dl == dr)
    {
        for(int i=l; i<=r; i++)
        {
            ans = max(ans, (sop[i].e-fac[dl].d)*(sop[i].q-fac[dl].p));
        }
        return;
    }
    int mid = (l + r) >> 1; ll res = 0;
    int dm = 0;
    for(int i=dl; i<=dr; i++)
    {
        if((sop[mid].e-fac[i].d)*(sop[mid].q-fac[mid].p) > res)
        {
            res = (sop[mid].e-fac[i].d)*(sop[mid].q-fac[mid].p);
            dm = i;
        }
    }
    solve(l, mid, dl, dm); solve(mid+1, r, dm, dr);
}

int main()
{
    //freopen("monye2.in", "r", stdin);
    
    m = read(); n = read();
    for(int i=1; i<=m; i++)
    {
        fac[i].p = read(); fac[i].d = read();
    }
    for(int i=1; i<=n; i++)
    {
        sop[i].q = read(); sop[i].e = read();
    }
    sort(fac+1, fac+1+m);
    sort(sop+1, sop+1+n);
    for(int i=1; i<=m; i++)
    {
        if(t1 == 0 || fac[i].d <= fac[q1[t1]].d) 
        {
            q1[++t1] = i; mind = min(mind, fac[i].d);
            minp = min(minp, fac[i].p);
        }
    }
    for(int i=1; i<=n; i++)
    {
        if(sop[i].e <= mind || sop[i].q <= minp) continue;//Del
        while(t2 > 0 && sop[i].e >= sop[q2[t2]].e)
        {
            t2--;
        }
        q2[++t2] = i;
    }
    solve(1, t2, 1, t1);
    printf("%lld\n", ans);

    return 0;
}

 看来没有太认真，我把直接的数组编号传进去了而不是栈的下标，如果传对的话，WA 70

#include <bits/stdc++.h>
  
using namespace std;
  
typedef long long ll;
const int maxn = 5e5 + 5;
const int N = 1e7 + 2;
const int mod = 1e9 + 7;
const int INF = 1061109567;
  
int m, n, q1[maxn], q2[maxn], t1, t2;
ll mind = INF, minp = INF, ans;
  
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}
  
struct Fac
{
    ll p, d;
    bool operator < (const Fac &T) const
    {
        return p < T.p;
    }
}fac[maxn];
  
struct Sop
{
    ll q, e;
    bool operator < (const Sop &T) const
    {
        return q < T.q;
    }
}sop[maxn];
  
void solve(int l, int r, int dl, int dr)
{
    if(l == r)
    {
        for(int i=dl; i<=dr; i++)
        {
            ans = max(ans, (sop[q2[l]].e-fac[q1[i]].d)*(sop[q2[l]].q-fac[q1[i]].p));
        }
        return;
    }
    if(dl == dr)
    {
        for(int i=l; i<=r; i++)
        {
            ans = max(ans, (sop[q2[i]].e-fac[q1[dl]].d)*(sop[q2[i]].q-fac[q1[dl]].p));
        }
        return;
    }
    int mid = (l + r) >> 1; ll res = 0;
    int dm = 0;
    for(int i=dl; i<=dr; i++)
    {
        if((sop[q2[mid]].e-fac[q1[i]].d)*(sop[q2[mid]].q-fac[q1[i]].p) > res)
        {
            res = (sop[q2[mid]].e-fac[q1[i]].d)*(sop[q2[mid]].q-fac[q1[i]].p);
            dm = i;
        }
    }
    solve(l, mid, dl, dm); solve(mid+1, r, dm, dr);
}
  
int main()
{
    //freopen("money.in", "r", stdin);
      
    m = read(); n = read();
    for(int i=1; i<=m; i++)
    {
        fac[i].p = read(); fac[i].d = read();
    }
    for(int i=1; i<=n; i++)
    {
        sop[i].q = read(); sop[i].e = read();
    }
    sort(fac+1, fac+1+m);
    sort(sop+1, sop+1+n);
    for(int i=1; i<=m; i++)
    {
        if(t1 == 0 || fac[i].d <= fac[q1[t1]].d) 
        {
            q1[++t1] = i; mind = min(mind, fac[i].d);
            minp = min(minp, fac[i].p);
        }
    }
    for(int i=1; i<=n; i++)
    {
        if(sop[i].e <= mind || sop[i].q <= minp) continue;//Del
        while(t2 > 0 && sop[i].e >= sop[q2[t2]].e)
        {
            t2--;
        }
        q2[++t2] = i;
    }
    solve(1, t2, 1, t1);
    printf("%lld\n", ans);
  
    return 0;
}

 我严重怀疑accoders卡抄题解，我敢肯定我绝对没有抄错交上去就TLE 40，除非我交带有查重标号的明显的COPY代码……有人遇到过类似的问题吗？

#include <bits/stdc++.h>
 
using namespace std;
 
typedef long long ll;
const int maxn = 1e5 + 3;
const int N = 1e7 + 2;
const int mod = 1e9 + 7;
const ll INF = 0x7ffffffffff;
 
int n, m, q1[maxn], q2[maxn], t1, t2;
ll ans;
 
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}
 
struct node 
{
    ll v, t;
    bool operator < (const node &T) const
    {
        return v < T.v;
    }
}fac[maxn], sop[maxn];
 
inline ll getans(int x, int y)
{
    if(sop[y].t < fac[x].t || sop[y].v < fac[x].v) return 0;
    return (sop[y].t-fac[x].t)*(sop[y].v-fac[x].v);
}
 
void solve(int l, int r, int dl, int dr)
{
    if(l > r || dl > dr) return;
    ll zwans;
    if(l == r)
    {
        for(int i=dl; i<=dr; i++)
        {
            zwans = getans(q1[l], q2[i]);
            ans = max(ans, zwans);
        }
        return;
    }
    if(dl == dr)
    {
        for(int i=l; i<=r; i++)
        {
            zwans = getans(q1[i], q2[dl]);
            ans = max(ans, zwans);
        }
        return;
    }
    int mid = (l + r) >> 1;
    ll nowans = 0; int id = 0;
    for(int i=dl; i<=dr; i++)
    {
        ll myans = getans(q1[mid], q2[i]);
        if(myans >= nowans) id=i, nowans=myans;
    }
    if(id == 0) return;
    ans = max(ans, nowans);
    solve(l, mid-1, dl, id);
    solve(mid+1, r, id, dr);
}
 
int main()
{
    m = read(); n = read();
    for(int i=1; i<=m; i++)
    {
        fac[i].v = read(); fac[i].t = read();
    }
    for(int i=1; i<=n; i++)
    {
        sop[i].v = read(); sop[i].t = read();
    }
    sort(fac+1, fac+1+m);
    sort(sop+1, sop+1+n);
    for(int i=1; i<=m; i++)
    {
        if(!t1) q1[++t1] = i;
        else
        {
            if(fac[i].t < fac[q1[t1]].t) q1[++t1] = i;
        }
    }
    for(int i=1; i<=n; i++)
    {
        while(t2 && sop[q2[t2]].t < sop[i].t) t2--;
        q2[++t2] = i;
    }
    //while(tal < t1 && fac[q1[tal]].t >= sop[q2[1]].t) tal++;
    while(t1 > 1 && fac[q1[t1]].v > sop[q2[t2]].v) t1--;
    solve(1, t1, 1, t2);
    printf("%lld\n", ans);
 
    return 0;
}

 我真的连变量名都没改，它再超时，好吧它又T了，真行真行真行……我就当我抄对了？？？无语啊

#include <bits/stdc++.h>
 
using namespace std;
 
typedef long long ll;
const int maxn = 1e5 + 3;
const int N = 1e7 + 2;
const int mod = 1e9 + 7;
const ll INF = 0x7ffffffffff;
 
int n, m;
ll ans;
struct Goods 
{
    ll val, dat;
    bool operator < (const Goods &G) const 
    {
        return val < G.val;
    }
}buy[maxn], sell[maxn];
int st1[maxn], st2[maxn], tp1, tp2;
 
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

inline ll getans(int x, int y)
{
    if(buy[y].dat < sell[x].dat && buy[y].val < sell[x].val) return 0;
    return (buy[y].dat - sell[x].dat)*(buy[y].val - sell[x].val);
}

inline void solve(int l, int r, int dl, int dr)
{
    if(l > r || dl > dr) return;
    ll zwans;
    if(l == r)
    {
        for(int i=dl; i<=dr; i++)
        {
            zwans = getans(st1[l], st2[i]);
            ans = max(ans, zwans);
        }
        return;
    }
    if(dl == dr)
    {
        for(int i=l; i<=r; i++)
        {
            zwans = getans(st1[i], st2[dl]);
            ans = max(ans, zwans);
        }
        return;
    }
    int mid = (l + r) >> 1;
    ll nowans = 0; int id = 0;
    for(int i=dl; i<=dr; i++)
    {
        ll myans = getans(st1[mid], st2[i]);
        if(myans >= nowans) id = i, nowans = myans;
    }
    ans = max(ans, nowans);
    solve(l, mid-1, dl, id);
    solve(mid+1, r, id, dr);
}

int main()
{
    m = read(); n = read();
    for(int i=1; i<=m; i++)
    {
        sell[i].val = read(); sell[i].dat = read();
    }
    for(int i=1; i<=n; i++)
    {
        buy[i].val = read(); buy[i].dat = read();
    }
    sort(sell+1, sell+1+m);
    sort(sell+1, sell+1+m);
    for(int i=1; i<=m; i++)
    {
        if(!tp1) st1[++tp1] = i;
        else 
        {
            if(sell[i].dat < sell[st1[tp1]].dat) st1[++tp1] = i;
        }
    }
    for(int i=1; i<=n; i++)
    {
        while(tp2 && buy[st2[tp2]].dat < buy[i].dat) --tp2;
        st2[++tp2] = i;
    }
    while(tp1 > 1 && sell[st1[tp1]].val > buy[st2[tp2]].val) --tp1;
    solve(1, tp1, 1, tp2);
    printf("%lld\n", ans);
 
    return 0;
}

真的是够了啊，够了，下一页还有我就不粘了，除了CV的之外，每一版都是重写的（重抄的），如果我信任我的抄题解技术，那就一定是accoders再搞鬼……致富之路是我走不上了……

想看正解到caorong的博客园里去找吧，然后你就会发现我真的是什么都没改就T了啊，TLE10分也是过分了啊，就算抄的也是正解啊，说起来还是hz的题库良心……

 update:上面本来有张图的，但是它太丑了，所以我把它删掉了。

可能是因为过了一天，accoders的记性不太好了，也可能是因为换了一篇题解，也可能是因为昨天真的抄错了一晚上，总之就是Cat终于不带查重标号的A了！！！

至于为什么可以二分——把题解上的式子乘开就说明它是对的，不过新的问题是为什么Chen_jr的题解不用考虑负负得正的情况，难道是大佬自带的AC光环？感觉如果加个判断的话更严谨一点，虽然但是我抄的时候什么都没改。

#include <bits/stdc++.h>
  
using namespace std;
  
typedef long long ll;
const int maxn = 5e5 + 5;
const int N = 1e7 + 2;
const int mod = 1e9 + 7;
const int INF = 1061109567;

int sta[maxn], stb[maxn], ta, tb, n, m;
ll ans;
  
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

struct node 
{
    ll val, day;
    bool operator < (const node &T) const 
    {
        return day < T.day;
    }
}a[maxn], b[maxn], ls[maxn];//ls就是用来临时储存的，把栈里的再传回来

void solve(int l, int r, int dl, int dr)
{
    if(l > r || dl > dr) return;
    int mid = (dl + dr) >> 1;
    int pos = 0;
    ll mx = -0x3f3f3f3f;
    for(int i=l; i<=r; i++)
    {
        ll nans = (b[mid].day-a[i].day)*(b[mid].val-a[i].val);
        if(nans > mx)
        {
            mx = nans; pos = i;
        }
    }
    ans = max(ans, mx);
    solve(l, pos, dl, mid-1);
    solve(pos, r, mid+1, dr);
}

int main()
{
    //freopen("monye2.in", "r", stdin);
    
    m = read(); n = read();
    for(int i=1; i<=m; i++)
    {
        a[i].val = read(); a[i].day = read();
    }
    for(int i=1; i<=n; i++)
    {
        b[i].val = read(); b[i].day = read();
    }
    sort(a+1, a+1+m); sort(b+1, b+1+n);
    for(int i=m; i>=1; i--)
    {
        while(ta && a[sta[ta]].val >= a[i].val) ta--;//时间递减，val递增
        sta[++ta] = i;
    }
    for(int i=1; i<=ta; i++)
    {
        ls[i] = a[sta[ta-i+1]];//时间递增，val递减
    }
    for(int i=1; i<=ta; i++)
    {
        a[i] = ls[i];
    }
    for(int i=1; i<=n; i++)
    {
        while(tb && b[stb[tb]].val <= b[i].val) tb--;
        stb[++tb] = i;
    }
    for(int i=1; i<=tb; i++) ls[i] = b[stb[i]];
    for(int i=1; i<=tb; i++) b[i] = ls[i];
    int mi = 0x3f3f3f3f, pa = 1, pb = 0;
    for(int i=1; i<=tb; i++)
    {
        while(pa <= ta && a[pa].day < b[i].day) mi = min((ll)mi, a[pa++].val);
        if(mi < b[i].val) ls[++pb] = b[i];
    }
    tb = pb;
    for(int i=1; i<=tb; i++)
    {
        b[i] = ls[i];
    }
    solve(1, ta, 1, tb);
    printf("%lld\n", ans);
  
    return 0;
}

 

问题 D: 【2022暑期集训8月13日】平衡树

 把每一课子树的最大alpha存到线段树上，单点修改求最大值就是当前节点为根的最大alpha。

换根操作非常神奇，预处理出每个点为根时它最大的子树和次大的子树，(在根是1的这棵树上可能还是它的父节点，所以不能在这时dfs，否则就乱套了)。第一遍dfs的时候把根是1的情况全处理完了，所以最先得到的是1作为根的最大alpha值，dfs2的顺序是从上到下，进入新的一层递归时是以当前节点为根，所以在进入之前要做好预处理，返回之前(其实也是一种进入)也要把size变成即将出现的情况。

本来是只有最大的子树有用，但是再换根的过程中可能最大的子树成为根了就贡献不上了，这时就需要次大的子树发挥作用。判断子树有多少的方法1.maxsize==size[x]-1? 2.cnt>1?

query之后cnt要减1，去掉x和v之间的连边，如果x能成为换根后给v有贡献的子树，才用它的子树大小更新答案，预处理的是换根前新根的子树，查询之前的那一次查的是根自己(整棵树)。

感觉最难的部分是：当它有两个及以上的子节点的时候，他任意子树的大小满足alpha，我想到了用cnt记录子树大小然后不算自己，可是想不到合法的子树的子树大小怎么影响答案，解决方案就是把每一个点能产生的贡献(感觉说是负贡献更形象)全都存起来。

#include <bits/stdc++.h>
  
using namespace std;
  
typedef long long ll;
const int maxn = 5e5 + 5;
const int N = 1e7 + 2;
const int mod = 1e9 + 7;
const int INF = 1061109567;

int n, k, size[maxn], si;
int mx[maxn], cmx[maxn], son[maxn];
long double ap[maxn];
  
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

struct node 
{
    int next, to;
}a[maxn<<1];
int head[maxn], len;

void add(int x, int y)
{
    a[++len].to = y; a[len].next = head[x];
    head[x] = len;
}

struct tree 
{
    long double t[maxn<<2];
    void modify(int x, int l, int r, int pos, long double val)
    {
        if(l == r) 
        {
            t[x] = val; return;
        }
        int mid = (l + r) >> 1;
        if(pos <= mid) modify(x<<1, l, mid, pos, val);
        else modify(x<<1|1, mid+1, r, pos, val);
        t[x] = max(t[x<<1], t[x<<1|1]);
    }
    long double query()
    {
        return t[1];
    }
}t;

void dfs1(int x, int fa)
{
    size[x] = 1;
    int mx = 0;
    for(int i=head[x]; i; i=a[i].next)
    {
        int v = a[i].to;
        if(v == fa) continue;
        dfs1(v, x);
        size[x] += size[v];
        mx = max(mx, size[v]);
    }
    //以1为根
    t.modify(1, 1, n, x, mx==size[x]-1?0:(long double)mx/size[x]);
}

void dfs2(int x, int fa)
{
    int cnt = 0;
    for(int i=head[x]; i; i=a[i].next)
    {
        int v = a[i].to; cnt++;//以x为根
        if(size[v] > mx[x])
        {
            cmx[x] = max(mx[x], cmx[x]);//次大的子树
            mx[x] = size[v];//最大的子树
            son[x] = v;
        }
        else cmx[x] = max(cmx[x], size[v]);
    }
    t.modify(1, 1, n, x, cnt>1?(long double)mx[x]/si:0);
    ap[x] = t.query(); cnt--;
    for(int i=head[x]; i; i=a[i].next)
    {
        int v = a[i].to;
        if(v == fa) continue;
        size[x] = si - size[v];//以v为根
        t.modify(1, 1, n, x, cnt>1?(son[x]==v?(long double)cmx[x]/size[x]:(long double)mx[x]/size[x]):0);
        dfs2(v, x);
    }
    size[x] = si-size[fa];//即将返回，以fa为根，做好准备
    t.modify(1, 1, n, x, cnt>1?(son[x]==fa?(long double)cmx[x]/size[x]:(long double)mx[x]/size[x]):0);
}

int main()
{
    n = read(); k = read();
    for(int i=1; i<n; i++)
    {
        int x = read(), y = read();
        add(x, y); add(y, x);
    }
    dfs1(1, 0); si = size[1];
    dfs2(1, 0); sort(ap+1, ap+n+1);
    int m = read(), las = 0;
    for(int i=1; i<=m; i++)
    {
        int a = read()^(las*k), b = read()^(las*k);
        printf("%d\n", las=upper_bound(ap+1, ap+n+1, (long double)a/b)-ap-1);
    }
  
    return 0;
}