关于卡特兰数

//声明：非原创
什么是卡特兰数？

明安图数，又称卡塔兰数，英文名Catalan number，是组合数学中一个常出现于各种计数问题中的数列。以中国蒙古族数学家明安图 (1692-1763)和比利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名，其前几项为（从第零项开始） : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …
卡特兰数的几何意义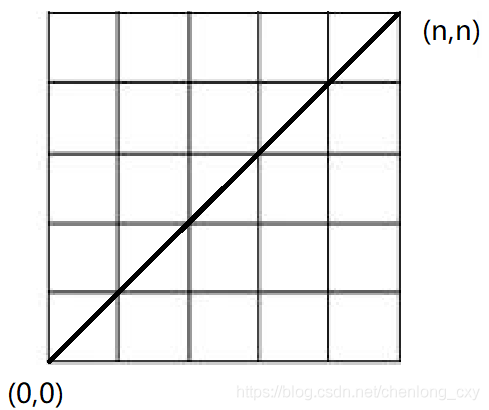

 

简单来说，卡特兰数就是一个有规律的数列，在坐标图中可以表示为：从原点(0,0)出发，每次向x轴或者y轴正方向移动1个单位，直到到达(n,n)点，且在移动过程中不越过第一象限平分线的移动方案总数。

 

卡特兰数公式推导

我们暂且先不考虑移动过程中不越过第一象限平分线这个约束条件，那么从(0,0)点到(n,n)点的过程中，我们总共需要向右移动n步，向上移动n步，一共2n步。我们可以理解为在2n步里面选出n步来向上移动，那么剩下的n步就是向右移动的步数，那么方案总数就是 C 2 n n C_{2n}^n C2nn​。

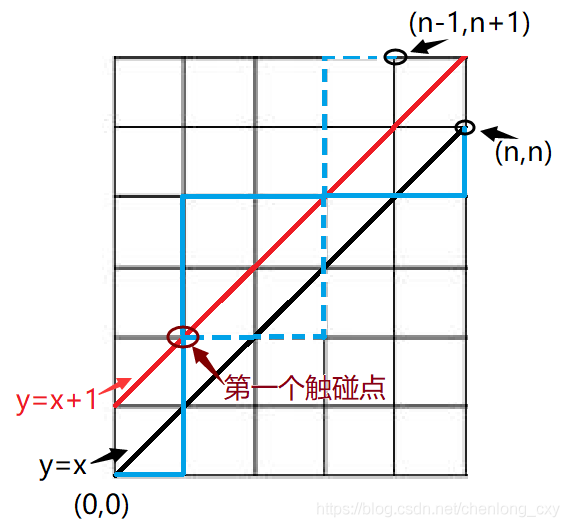
现在，我们来看看如何解决不越过第一象限平分线这个问题。仔细想想，不越过第一象限平分线也就等价于不触碰到 y = x + 1 y=x+1 y=x+1这条直线。而我们如果把触碰到了直线 y = x + 1 y=x+1 y=x+1的路线的第一个与 y = x + 1 y=x+1 y=x+1的触碰点之后的路线关于直线 y = x + 1 y=x+1 y=x+1对称，并画出对称后的路线
在这里插入图片描述
我们会发现触碰到了直线 y = x + 1 y=x+1 y=x+1的路径的终点都变成了点(n-1,n+1)。也就是说，从(0,0)点到(n,n)点的路线当中触碰了直线 y = x + 1 y=x+1 y=x+1的路线条数与从(0,0)点到(n-1,n+1)点的路线条数的数量是相等的。于是从(0,0)点到(n,n)点的非法路径条数为 C 2 n n + 1 C_{2n}^{n+1} C2nn+1​。

综上所述，从(0,0)点到(n,n)点满足条件的路径数为 C 2 n n C_{2n}^n C2nn​- C 2 n n + 1 C_{2n}^{n+1} C2nn+1​。

通过化简，公式可以简化为：

 

除了这个通项公式之外，卡特兰数还有一个由该通项公式推导而来的递推公式：