leetcode回溯法典型例题：39.组合总和、40组合总和 II、46.全排列、47.全排列 II

39.组合总和

思路

构建组合

使用递归的方式构建出所有组合。由题意可知，元素可以无限取用，所以我们构建的时候每确定一个数字，进入更深层递归的时候，每个数字都可以取用（此时仅从构建组合的角度进行理解）。
对重复元素进行剪枝

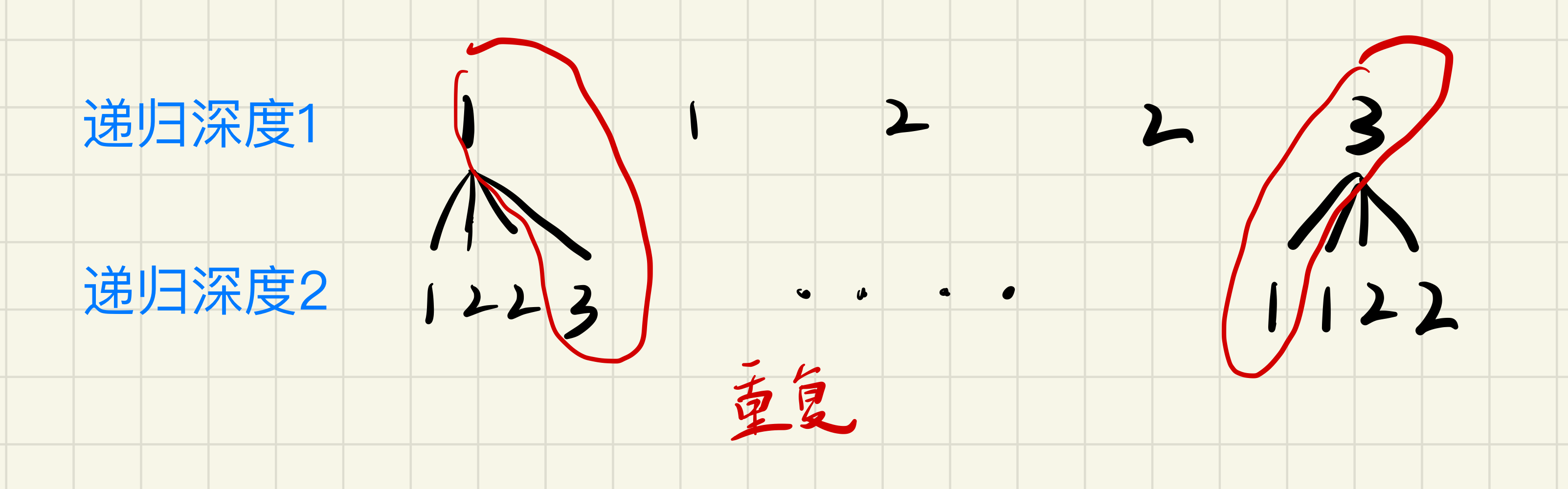
由题意可知，[1, 1, 2]与[1, 1, 2]属于同一个组合，所以构建组合的时候，遇到下图这种情况，需要剪枝：

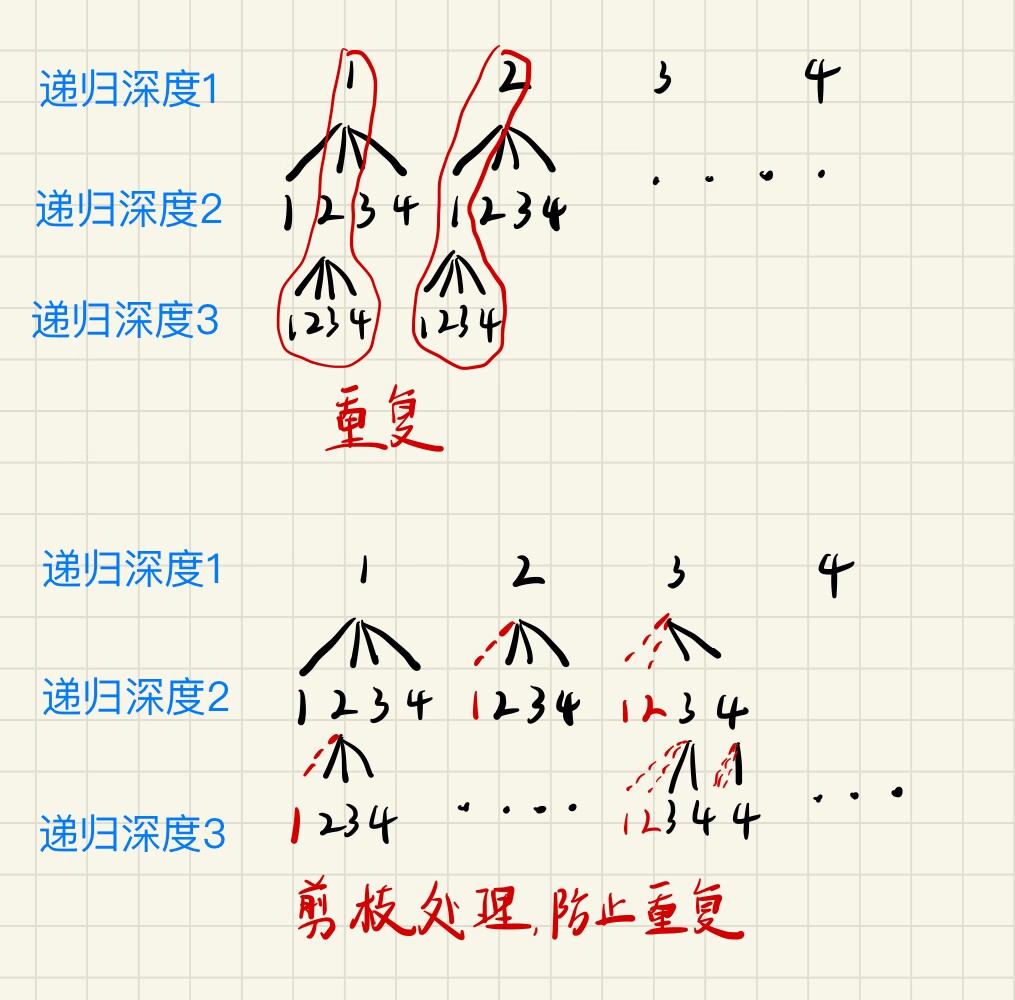
剪枝完成之后如下图：
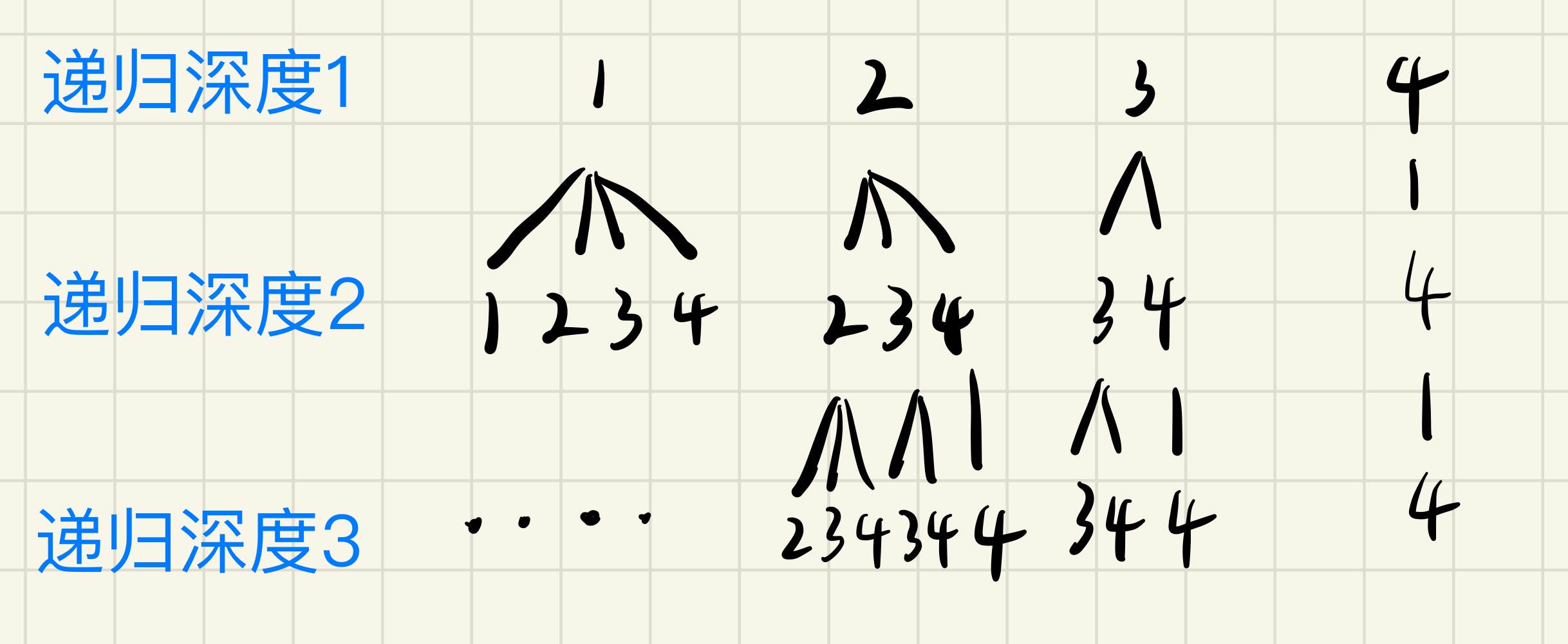
对数值过大组合进行剪枝

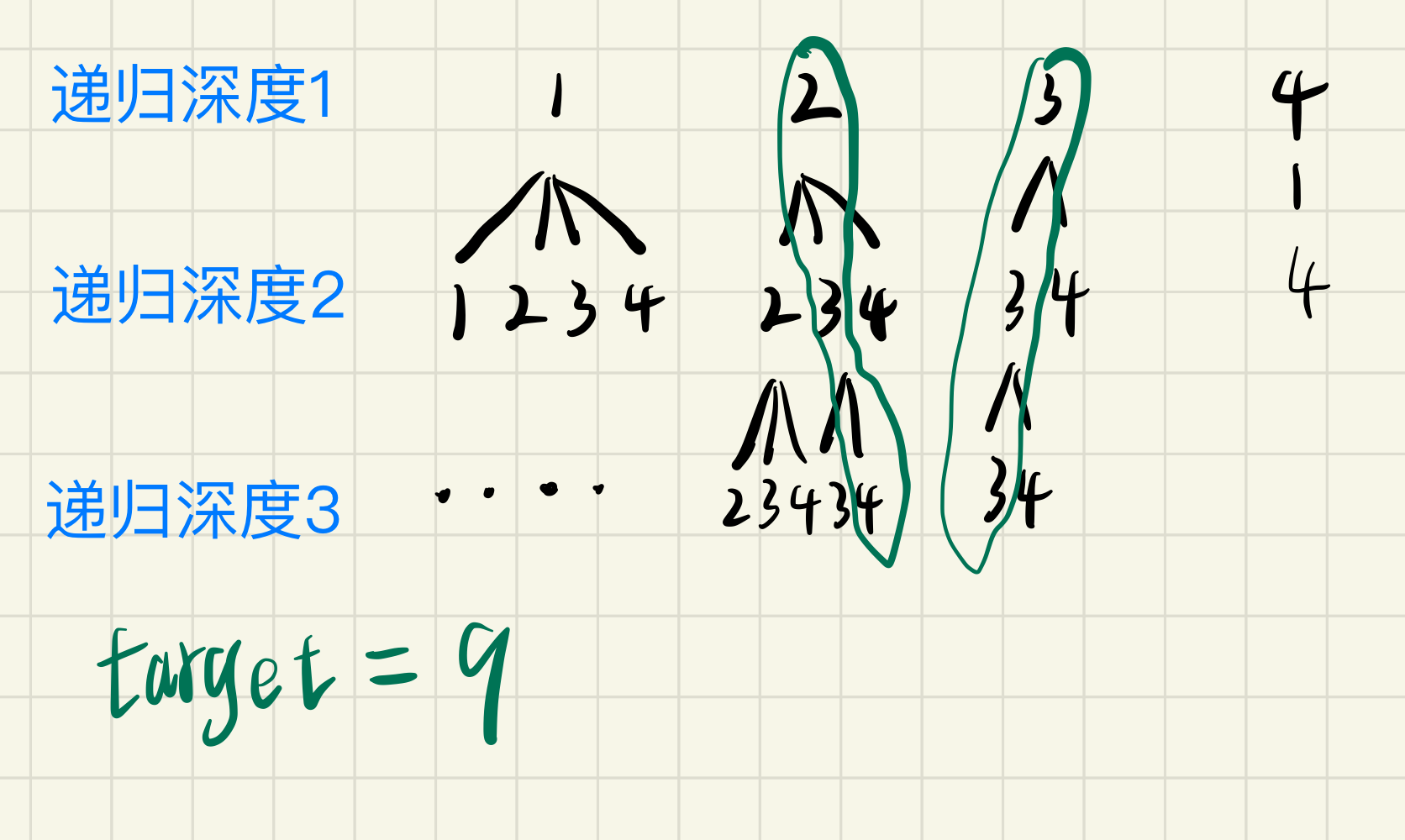
当某分支上的数据累加值已经超出了目标值，也需要剪枝
对数值刚好等于target的组合填充进res中

代码实现

关键点：通过分析“对重复元素剪枝”这个步骤，我们可以知道如果设置一个最小起始下标minIndex，并且在每轮递归的for循环中，只从minIndex开始添加值。因为这样就能保证下一个取用的元素为当前元素或之后的元素，所以能够实现“对重复元素剪枝”。

function combinationSum(candidates: number[], target: number): number[][] {
  const res: number[][] = [];
  const trackArr: number[] = [];
  let trackSum = 0;

  function dfs(minIndex: number) {
    if (trackSum > target) return; // 数据过大，剪枝
    if (trackSum === target) return res.push([...trackArr]); // 找到元素，返回

    for (let i = minIndex; i < candidates.length; i++) {
      trackArr.push(candidates[i]);
      trackSum += candidates[i];
      dfs(i);
      trackArr.pop();
      trackSum -= candidates[i];
    }
  }
  dfs(0);

  return res;
}

gpt总结

这段代码实现了寻找数组中所有可以使数字和为给定目标数的组合的算法，不同于combinationSum2，这里的每个数字在每个组合中可以重复使用。通过深度优先搜索（DFS）与回溯的方法，算法探索所有可能的组合以找到满足条件的解。以下是对该算法的详细分析：

算法逻辑：通过深度优先搜索（DFS），算法尝试所有可能的数字组合来寻找总和等于target的组合。为了避免重复的组合，搜索时会限制下一个可选数字的最小索引为minIndex，即当前元素或之后的元素。这个过程中，如果当前组合的总和超过了目标值，则提前终止搜索（剪枝），以提高搜索效率。找到有效的组合后，将其复制并添加到结果数组res中。
变量解释：
- candidates：输入数组，包含所有候选数字。
- target：目标和。
- res：存储找到的所有符合条件的组合。
- trackArr：当前搜索路径上的数字组合。
- trackSum：当前trackArr中数字的总和。
- minIndex：当前递归调用可以选择的最小候选数字索引，用于确保组合中的数字是基于非递减顺序的。
关键代码分析：
- if (trackSum > target) return;：当当前路径上的数字总和超过目标值时，提前终止当前路径的搜索。
- if (trackSum === target) return res.push([...trackArr]);：找到一个总和等于目标值的组合时，将其添加到结果集中。
- for (let i = minIndex; i < candidates.length; i++) {...}：从minIndex开始，遍历所有可能的候选数字，并尝试将它们添加到当前路径trackArr中，之后递归地继续搜索。
- dfs(i);：递归调用自身来继续搜索，传入的i保证了数字可以被重复选择。
性能分析：
- 时间复杂度：由于是组合问题，且每个数字可以重复使用，最坏情况下的时间复杂度接近O(2^N)，N为candidates长度。但实际上，由于剪枝和组合的特性，实际时间复杂度会低于此估计。
- 空间复杂度：O(N)，N为递归的最大深度，主要是递归栈的空间开销以及trackArr的空间开销。
适用场景：这个算法适用于需要从一个集合中选择若干元素（元素可以重复选择），使其总和达到特定目标值的场景。它在解决组合问题、编程竞赛、算法面试等场合中非常有用，特别是在需要考虑元素重复使用的情况下。

40.组合总和 II

40. 组合总和 II - 力扣（LeetCode）

思路

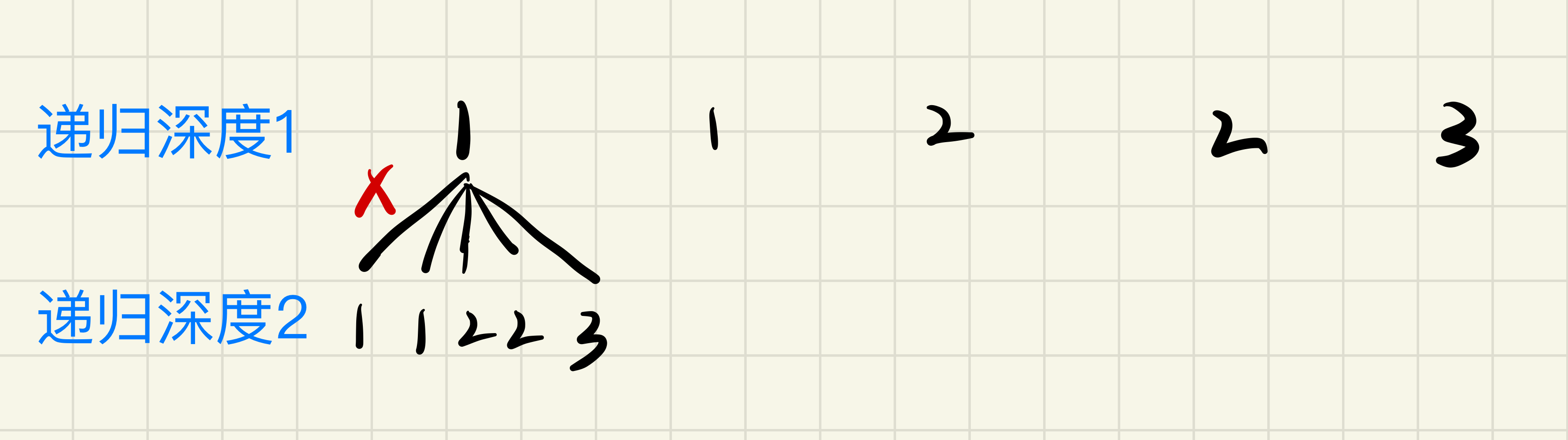
递归时排除已选元素，因为题目限制每个数字只能使用一次
对重复元素剪枝

同上题39.组合总和思路“2.对重复元素进行剪枝”
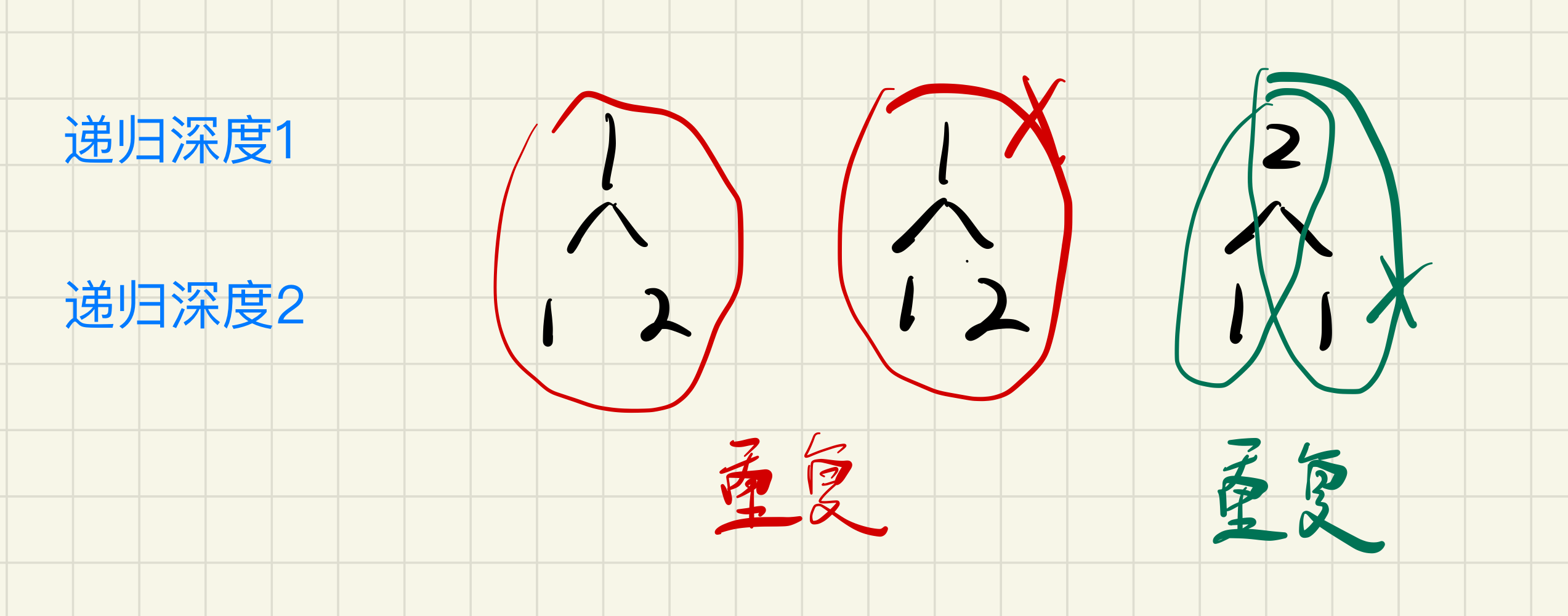
对同级且重复的非首位的元素剪枝

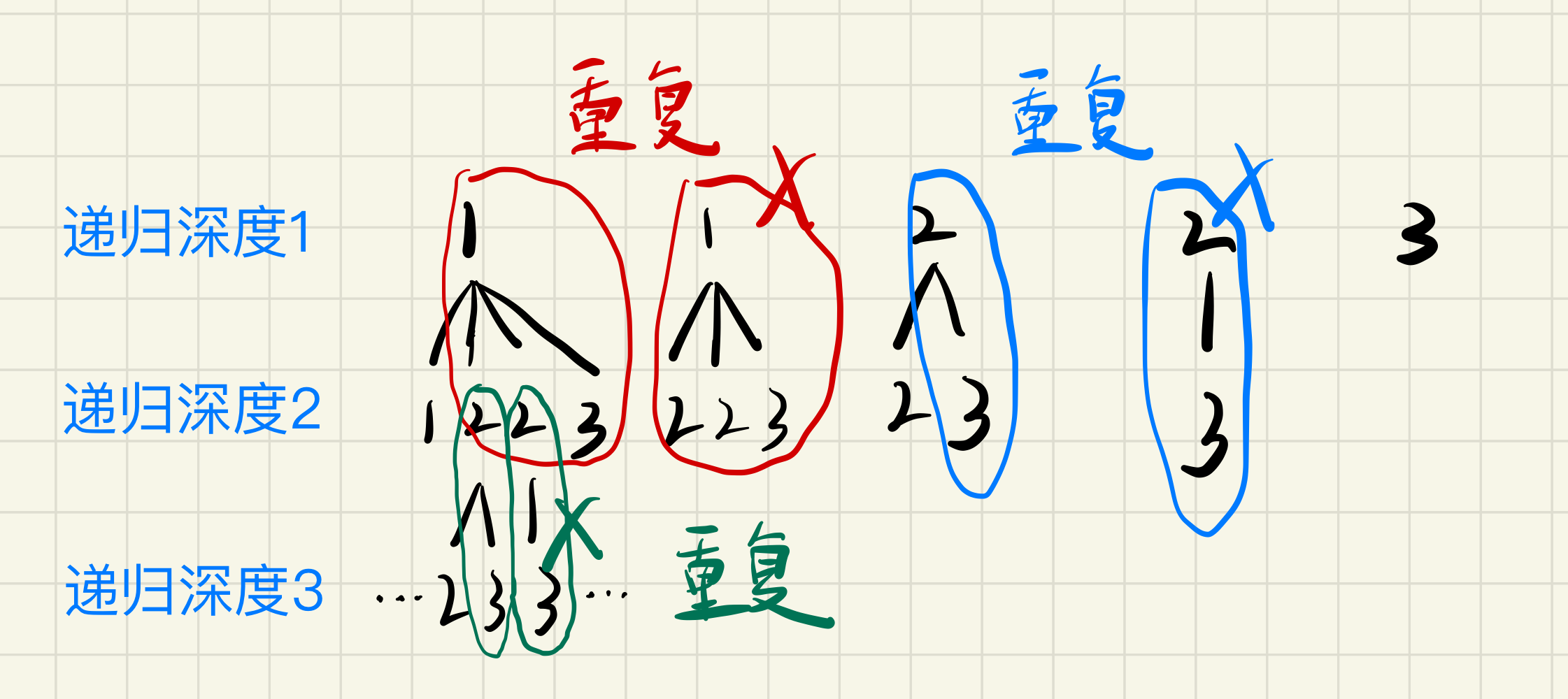
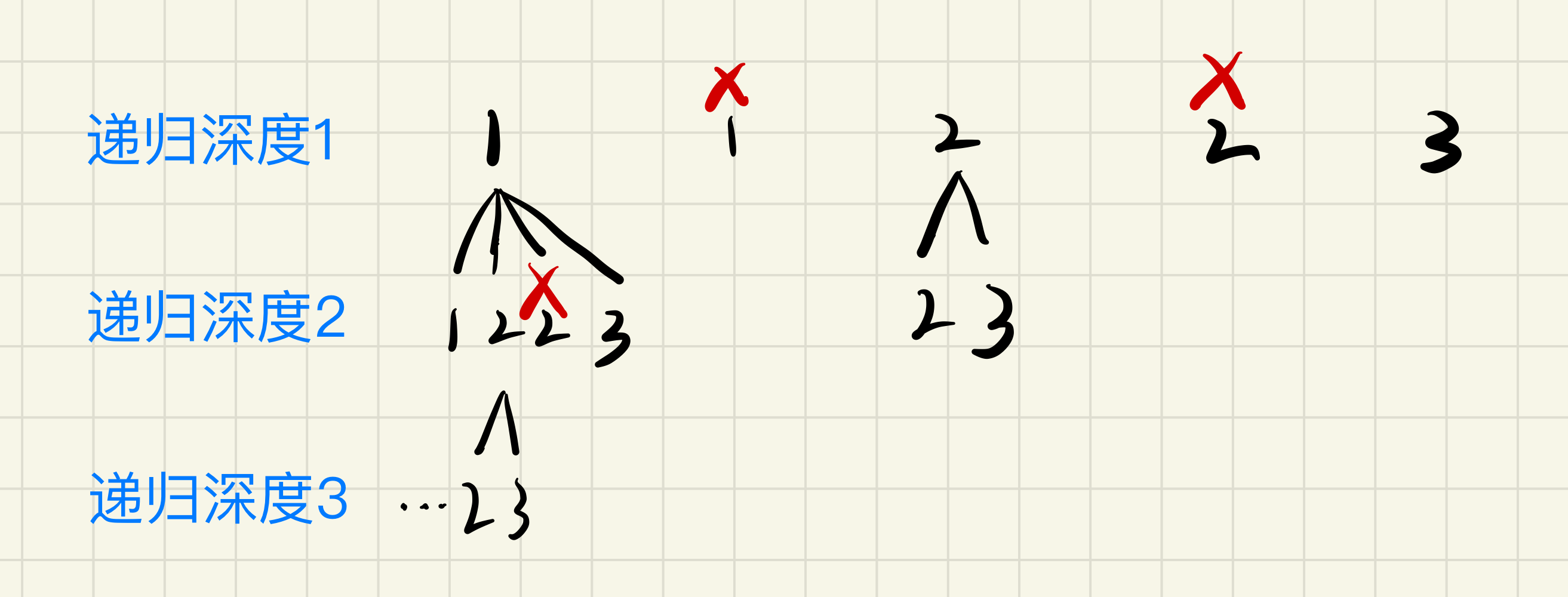
为了方便的实现，我们首先可以对题目提供的candidates数组进行排序，这样同级且相同的元素就会相邻，便于我们剪枝。

注意：一定是同级非首位的元素才会被剪枝。例如下图中，递归深度为2的时候，左数第一个1就不能剪枝，虽然在排序之后的candidates数组中，它是数组中的第二个1（在candidates数组中是重复的非首位的元素）。但是它在递归深度为2的时候不是一个重复元素，在这里它是第一次被添加进结果数组，所以它不可剪枝。

代码实现

代码实现基本与39.组合总和相同，主要不同点在于不允许使用重复元素，所以递归调用的时候是dfs(i + 1)；还有遇到重复数字的剪枝（跳过）逻辑：while (minIndex !== i && candidates[i] === candidates[i - 1]) i++;

function combinationSum2(candidates: number[], target: number): number[][] {
  const res: number[][] = [];
  const trackArr: number[] = [];
  let trackSum: number = 0;
  candidates.sort((a, b) => a - b);

  function dfs(minIndex: number) {
    if (trackSum > target) return; // 数据过大，剪枝
    if (trackSum === target) return res.push([...trackArr]); // 找到元素，返回

    for (let i = minIndex; i < candidates.length; i++) {
      while (minIndex !== i && candidates[i] === candidates[i - 1]) i++; // 遇到重复数字，跳过（如果是本轮第一个，则不跳过）
      if (candidates[i] === undefined) break;
      trackArr.push(candidates[i]);
      trackSum += candidates[i];
      dfs(i + 1);
      trackArr.pop();
      trackSum -= candidates[i];
    }
  }
  dfs(0);

  return res;
}

gpt总结

这个代码段是combinationSum2函数的另一个实现，旨在从给定数组candidates中找出所有唯一的组合，这些组合的数字总和等于目标数target。与前述combinationSum函数相比，此版本特别强调每个数字在每个组合中只能使用一次，并且需要去除结果中的重复组合。以下是对此版本的详细分析：

算法逻辑：首先，将输入的数组candidates进行排序，这样做既可以帮助后续的去重操作，也能有效地实现剪枝，避免无效的搜索。算法通过深度优先搜索（DFS）遍历所有可能的数字组合。在搜索过程中，如果当前组合的数字总和超出目标值，则终止当前路径的进一步探索。如果找到一个总和等于目标值的组合，则将其添加到结果集中。为了避免重复的组合，算法在遇到连续重复的数字时，只在每组数字的第一个实例上进行递归搜索。
变量解释：
- candidates：排序后的输入数组。
- target：目标和。
- res：存储所有符合条件的唯一组合。
- trackArr：当前路径上的数字组合。
- trackSum：当前路径上数字的总和。
关键代码分析：
- candidates.sort((a, b) => a - b);：对输入数组进行排序。
- while (minIndex !== i && candidates[i] === candidates[i - 1]) i++;：跳过连续的重复数字，以避免产生重复的组合。但是，如果是本轮循环的第一个数字（即minIndex === i），则不跳过。
- if (trackSum === target) return res.push([...trackArr]);：如果当前路径的数字总和等于目标值，则将其添加到结果集中。
- dfs(i + 1);：递归调用dfs函数，以i + 1作为下一个数字的最小索引，保证每个数字只使用一次。
性能分析：
- 时间复杂度：由于需要遍历所有可能的组合并且有去重逻辑，时间复杂度最坏情况下为O(2^N)，其中N为candidates的长度。排序操作的时间复杂度为O(NlogN)。因此，总体时间复杂度考虑排序和搜索为O(NlogN + 2^N)。
- 空间复杂度：O(N)，主要是递归栈空间的开销以及路径记录数组trackArr的空间开销。
适用场景：该算法适用于需要从一个集合中选择若干元素（元素只能使用一次），使其总和达到特定目标值的场景。它在解决组合问题、编程竞赛、算法面试等情形中非常有用，尤其是在需要考虑去除结果中重复组合的情况下。

46.全排列

46. 全排列 - 力扣（LeetCode）

思路

由题意可知，全排列不能含有重复数字，所以对重复数字剪枝

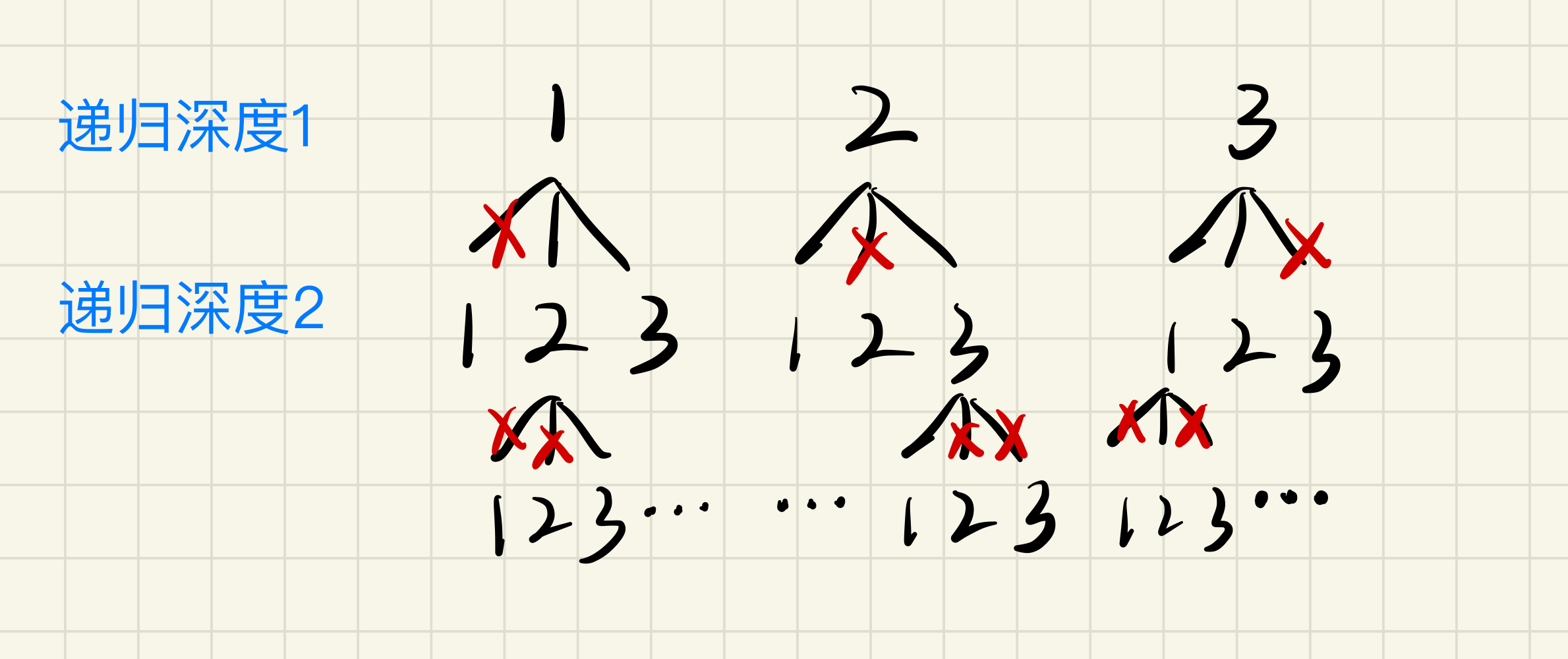
剪枝完成

代码实现

使用Set实现了“追踪数组”的功能，jsSet使用哈希表实现，一般数据量下Set.prototype.has方法比Array.prototype.includes更快些

function permute(nums: number[]): number[][] {
  const res: number[][] = [];
  const trackSet: Set<number> = new Set();
  const length = nums.length;

  function dfs() {
    if (trackSet.size === length) return res.push(Array.from(trackSet));

    for (let i = 0; i < length; i++) {
      const num = nums[i];
      if (trackSet.has(num)) continue; // 已添加过，剪枝

      trackSet.add(num);
      dfs();
      trackSet.delete(num);
    }
  }
  dfs();

  return res;
}

gpt总结

这段代码实现了一个生成给定数组所有可能排列的算法，使用了深度优先搜索（DFS）与回溯的方法。这种算法通过遍历数组并记录路径来探索所有可能的排列。下面是对该算法的详细分析：

算法逻辑：首先，初始化一个空的结果数组res来存储所有排列，以及一个Set对象trackSet来记录当前排列路径上的数字。算法通过一个dfs函数来递归地构建排列，每次递归时尝试添加还未在当前排列中的数字。当trackSet的大小等于输入数组nums的长度时，意味着构建了一个完整的排列，将其添加到res中。dfs函数通过遍历nums数组并尝试将每个数字添加到当前排列中来实现这一过程。如果一个数字已经在trackSet中（即已经被添加到当前路径），则跳过当前迭代，以避免重复。这种方法确保了探索所有不同的排列组合。
变量解释：
- res：存储所有可能排列的结果数组。
- trackSet：记录当前路径（即当前排列）的集合。使用Set是为了方便地检查某个数字是否已经被添加到当前路径。
- length：输入数组nums的长度，用于判断何时完成一个排列的构建。
- num：当前迭代尝试添加到排列中的数字。
关键代码分析：
- if (trackSet.size === length) return res.push(Array.from(trackSet));：检查当前路径长度是否等于nums长度，如果是，则将当前路径转换为数组并添加到结果中。
- if (trackSet.has(num)) continue;：如果当前数字已经在路径中，则跳过当前迭代。
- trackSet.add(num);：将当前数字添加到路径中。
- dfs();：递归调用dfs函数，继续构建排列。
- trackSet.delete(num);：回溯，即从路径中移除最后添加的数字，以尝试下一个数字。
性能分析：
- 时间复杂度：O(N!)，其中N为数组nums的长度。这是因为生成排列的数量为N的阶乘，每个排列构建过程中需要O(N)时间来复制路径。
- 空间复杂度：O(N)，主要空间开销来源于递归栈（深度最多为N）和路径记录（最长为N）。
适用场景：这个算法适用于需要求解一个集合所有可能排列的场景，如解决排列问题、编程竞赛、算法面试等。它能够有效地探索并生成一个数组的所有排列，对于算法学习和实践具有重要意义。

47.全排列 II

47. 全排列 II - 力扣（LeetCode）

思路

对重复数字剪枝

同上47.全排列思路“1.对重复数字剪枝”
对同级且重复的非首位的元素剪枝

同上40.组合总和 II思路“对同级且重复的非首位的元素剪枝”

代码实现

!trackIndexSet.has(i - 1)表示当前元素的上一个元素没有进入本轮数据的添加。也就是说当前元素与上一个元素处于同层。
nums[i - 1] === nums[i]，则说明当前元素是一个重复元素，并且是一个非首位元素。

当两个条件都满足的时候，此元素是一个“同级且重复的非首位的元素”，需要剪枝

function permuteUnique(nums: number[]): number[][] {
  const res: number[][] = [];
  const trackIndexSet: Set<number> = new Set();
  const length = nums.length;
  nums.sort((a, b) => a - b);

  function dfs() {
    if (length === trackIndexSet.size) return res.push(Array.from(trackIndexSet).map((index) => nums[index]));

    for (let i = 0; i < length; i++) {
      const num = nums[i];
      if (trackIndexSet.has(i)) continue; // 已添加过，剪枝
      if (!trackIndexSet.has(i - 1) && nums[i - 1] === num) continue; // 对同级且重复的非首位的元素剪枝

      trackIndexSet.add(i);
      dfs();
      trackIndexSet.delete(i);
    }
  }
  dfs();

  return res;
}

gpt总结

这段代码实现了一个寻找数字数组所有不重复排列的算法。现在，我将按照指定的结构进行分析：

算法逻辑

这个算法首先将输入数组排序，以便于后续的去重处理。通过深度优先搜索（DFS）遍历所有可能的排列组合。为了确保不会产生重复的排列，算法使用了一个集合（trackIndexSet）来记录当前排列中已选择的元素索引。在遍历过程中，如果一个元素与它前面的元素相同，并且前面的元素还未被加入到当前的排列中，那么这个元素就会被跳过（这是为了去重）。每当集合中的元素数量等于原数组的长度时，就会将当前的排列加入到结果列表中。
变量解释
- res：用来存储所有不重复的排列结果，初始化为空列表。
- trackIndexSet：一个集合，用于存储当前排列中已选择的元素的索引。
- length：输入数组 nums 的长度。
- nums：输入的数字数组，在函数开始处被排序，以便于后续的去重处理。
- i：循环中的变量，表示当前遍历到的元素索引。
- num：当前遍历到的元素值。
关键代码分析
- nums.sort((a, b) => a - b)：对输入数组进行排序，这是去重的前提。
- if (trackIndexSet.has(i)) continue：如果当前索引已经被选择，则跳过，以避免在同一排列中重复使用相同的元素。
- if (!trackIndexSet.has(i - 1) && nums[i - 1] === num) continue：去重的关键逻辑。如果当前元素与前一个元素相同，并且前一个元素还没有被选择，那么就跳过当前元素。这样做是为了避免产生重复的排列。
- dfs()：深度优先搜索的递归函数，用于探索所有可能的排列。
性能分析
- 时间复杂度：最坏情况下为O(n!)，因为需要遍历输入数组的所有可能排列。但实际上由于去重逻辑的存在，性能会比O(n!)好。
- 空间复杂度：O(n)，主要是递归栈的空间开销和trackIndexSet的空间开销。
适用场景
- 该算法适用于需要从一组可能包含重复数字的集合中找出所有不重复的排列组合的情况。例如，可以用在解决一些排列组合问题、编程竞赛题目中，或者任何需要此类操作的算法设计中。

核心思路

我们应当对题目提供的初始数组进行递归的处理，递归之后，先暂定更深层的递归可以选用初始数组中的所有元素
分析题目给出的限制条件，进行各种剪枝操作

提示：trackArr可以通过dfs函数传递，但是这样的话，每次递归都需要传递一个新的数组（否则会导致res中的所有元素指向同一个数组）。所以可以利用递归回溯的特性，进入更深层递归之前，将当前for循环选中的元素push进trackArr；跳出更深层递归之后，再将元素pop出trackArr

posted @ 2024-03-13 17:48 Cat_Catcher 阅读(54) 评论(0) 编辑收藏举报

刷新页面返回顶部

CatCatcher

leetcode回溯法典型例题：39.组合总和、40组合总和 II、46.全排列、47.全排列 II

39.组合总和

思路

代码实现

gpt总结

40.组合总和 II

思路

代码实现

gpt总结

46.全排列

思路

代码实现

gpt总结

47.全排列 II

思路

代码实现

gpt总结

核心思路

公告