leetcode 146/ LCR 031 LRU 缓存

146. LRU 缓存

LCR 031. LRU 缓存

题目描述

请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。

实现 LRUCache 类：

• LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
• int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
• void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

提示：

• 1 <= capacity <= 3000
• 0 <= key <= 10000
• 0 <= value <= 105
• 最多调用 2 * 105 次 get 和 put

解题思路

1. get、put需要以O(1)的时间复杂度执行

   根据此描述，可以想到使用Map（或者Object），通过映射的方式获取、添加关键字。

2. 缓存存在最大容量，需要在达到最大容量的时候，将最老的关键字删除

   根据此描述，可以想到使用一种有序的数据结构将关键字之间的顺序保存下来。这种数据结构在修改元素顺序、添加新元素、删除元素时的复杂度都是O(1)，那么双向链表在这里是最合适的。

3. 具体分析类中需要什么方法，各个方法的作用是什么

   1. get方法：根据key值获取value

      • 根据key查询Map，如果元素未保存过，则返回-1；

      • 根据key查询Map，如果元素保存过，则返回该key对应的value，并且需要将此key对应的链表节点提到最前（类似于将一摞书中抽出一本，放在最顶端；体现在链表中，就是将一个节点移动到链表头部）。

   2. put方法：根据key存放value

      • 根据key查询Map，如果元素已保存过，则更新节点的value，将此key对应的链表节点提到最前
      • 根据key查询Map，如果元素未保存过，则在链表起点处创建新节点。如果超过了最大容量，还要考虑删除尾节点。

   3. 根据分析上述操作，可以封装方法：

      • #moveToFirst：将此key对应的链表节点提到最前
      • #putInList：在链表起点处创建新节点

双向链表操作关键点

1. dummyNode

   为了处理数据结构操作中的边界条件，避免了对空数据结构的特殊处理，从而简化了代码的编写和逻辑。通过使用哑节点，开发者可以更加专注于核心逻辑的实现，而不是花费过多时间在处理边界条件上。

2. 移动节点（#moveToFirst：）
   

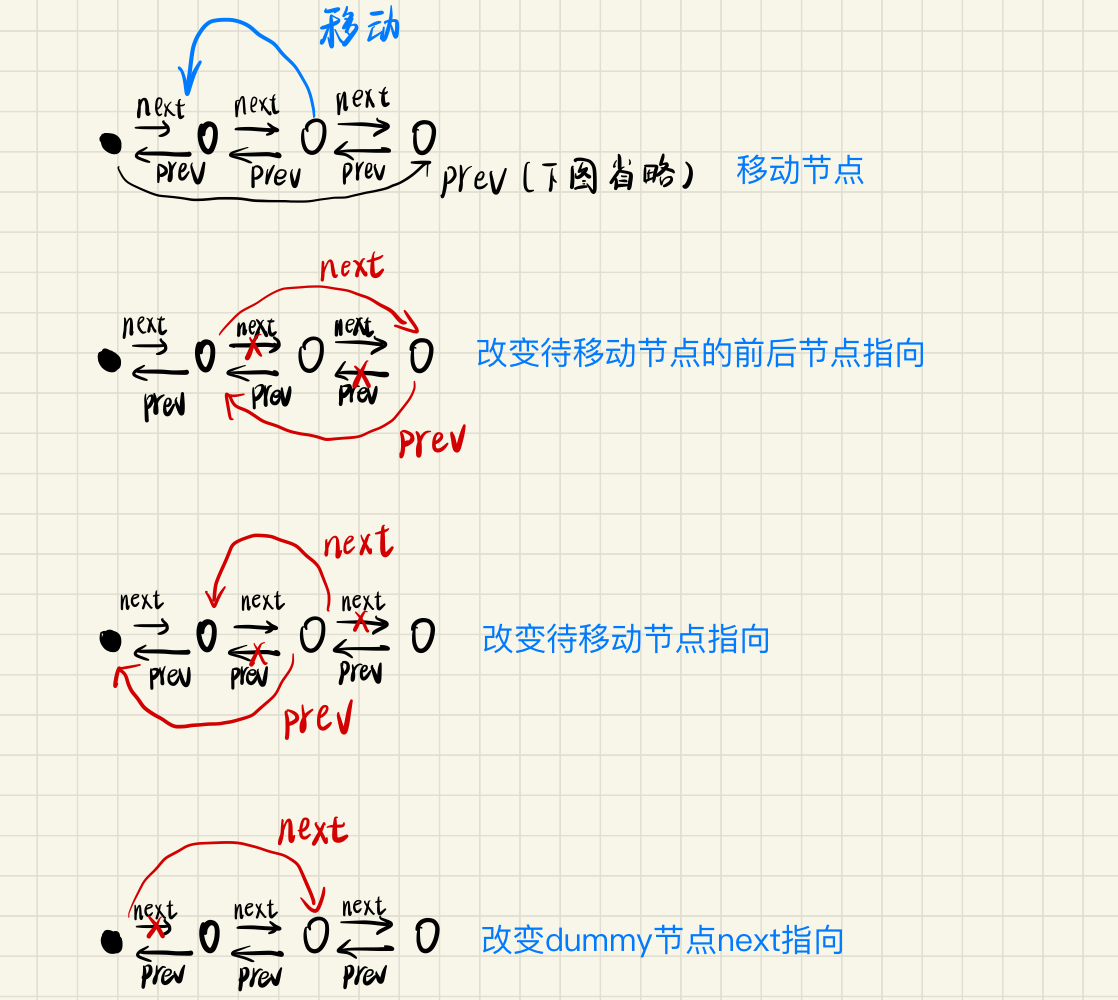
3. 插入节点（#putInList：）
   

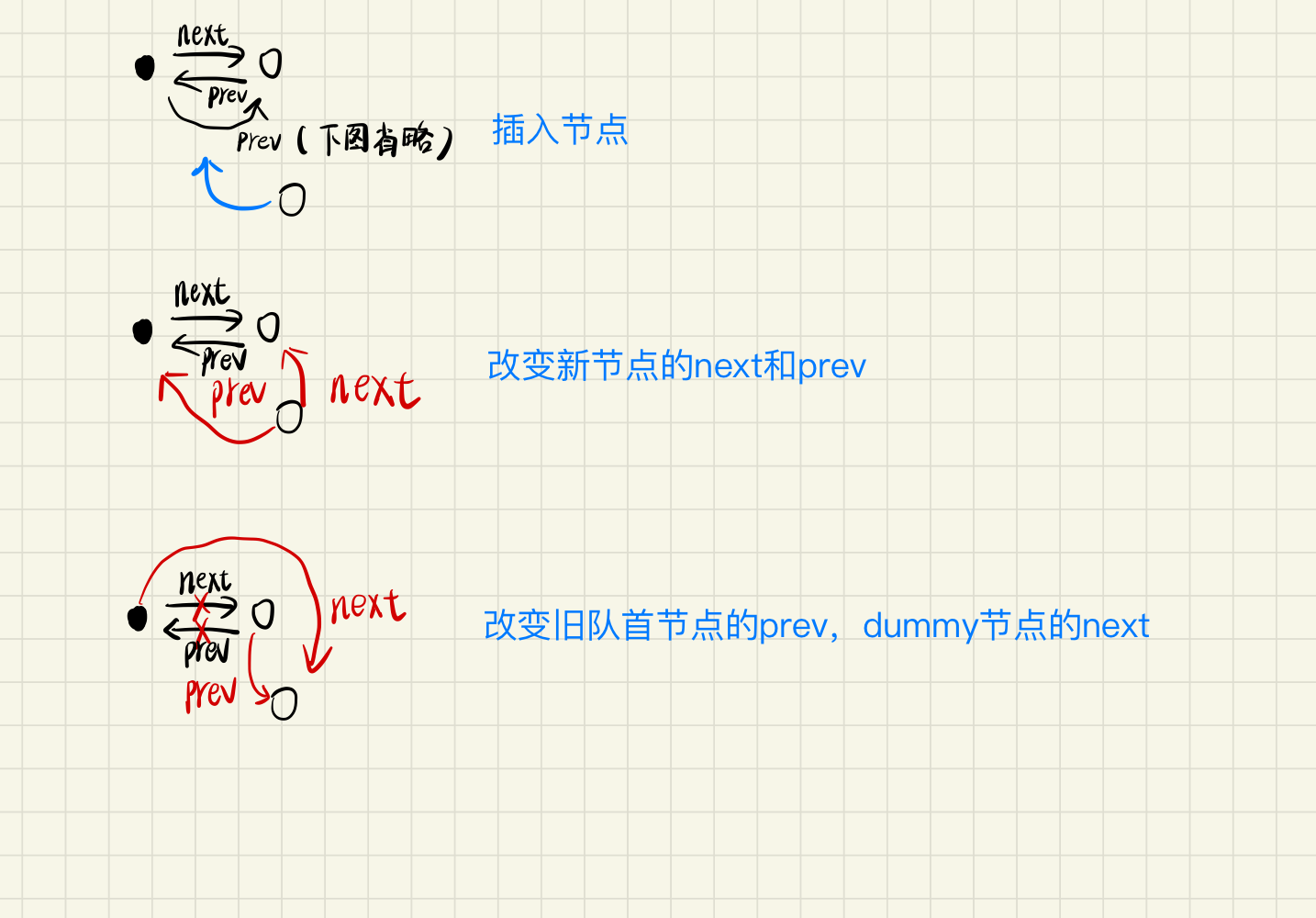
4. 删除节点
   

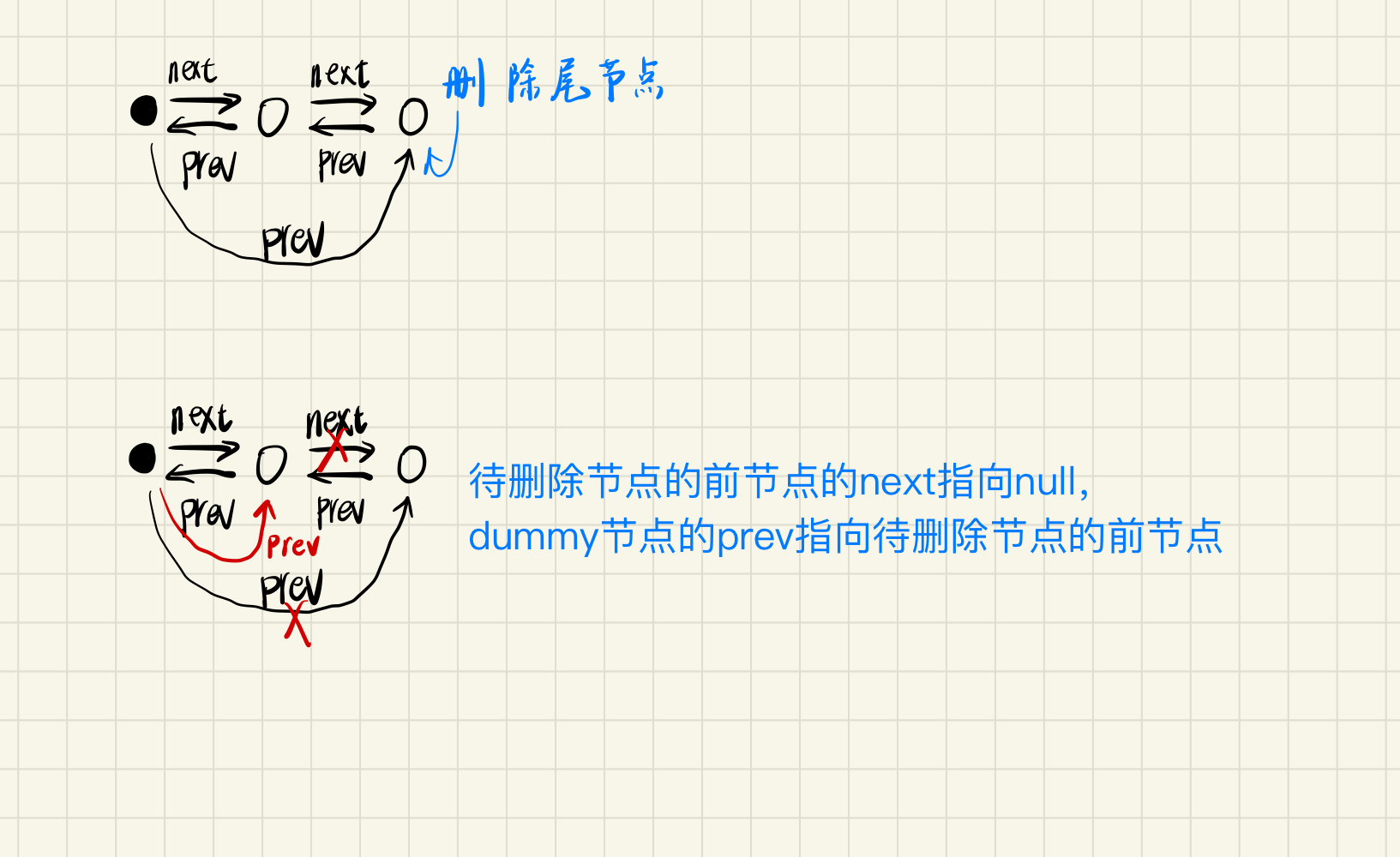
代码实现&gpt总结

这段代码实现了一个基于链表和哈希表的最近最少使用（LRU）缓存机制。下面是对该代码的分析：

1. 算法逻辑： LRUCache利用双向链表和哈希表（Map）相结合的方式，实现了快速的访问和更新缓存数据的能力。链表用于表示数据的使用顺序，最近使用的节点位于链表头部，而最久未使用的节点位于链表尾部。哈希表则存储键和对应节点的引用，以支持O(1)时间复杂度的访问。当缓存达到其容量上限时，最久未使用的数据会被移除。
2. 变量解释：
   • #capacity：缓存的最大容量。
   • #dummyNode：一个哨兵节点（或称虚拟节点），其next属性指向链表头部，prev属性指向链表尾部，用以简化边界条件处理。
   • #nodeMap：哈希表，存储键与节点引用的映射，支持快速访问和检查是否存在某键。
   • Node类的key、val：节点存储的键和值。
   • Node类的next、prev：指向链表中下一个和上一个节点的指针。
3. 关键代码分析：
   • #putInList方法：在链表头部插入新节点，表示最近使用。
   • #moveToFirst方法：将一个已存在的节点移动到链表头部，更新其为最近使用状态。
   • get方法：通过键获取值，如果找到对应的节点，则将其移动到链表头部，表示该数据最近被使用过。
   • put方法：插入或更新键值对。如果键已存在，更新其值并移动到链表头部；如果键不存在，先检查当前容量，如果未满，则直接在链表头部插入新节点，否则，移除链表尾部节点（最久未使用的数据），然后将新节点插入头部。
4. 性能分析：
   • 时间复杂度：对于get和put操作，由于哈希表的存在，时间复杂度都是O(1)。
   • 空间复杂度：O(N)，N为缓存的容量，即哈希表和双向链表存储空间的开销。
5. 适用场景： LRUCache适用于需要快速访问最近使用的数据的场景，如Web服务器缓存页面，操作系统缓存文件信息等。其目的是保证高效的数据访问，同时在达到预设容量限制时，能自动淘汰最久未使用的数据，保持缓存的有效性和高性能。

class Node {
  key: number;
  val: number;
  next: Node | null;
  prev: Node | null;
  constructor(key: number, val: number, prev: Node | null, next: Node | null) {
    this.key = key;
    this.val = val;
    this.next = next;
    this.prev = prev;
  }
}

class LRUCache {
  #capacity: number;
  #dummyNode: Node;
  #nodeMap: Map<number, Node>;
  // 将节点插入到首位（#dummyNode之后）
  #putInList(key: number, value: number) {
    const newNext = new Node(key, value, this.#dummyNode, null);
    this.#nodeMap.set(key, newNext);
    const oldNext = this.#dummyNode.next as Node;
    newNext.next = oldNext;
    this.#dummyNode.next = newNext;
    oldNext.prev = newNext;
  }
  // 将节点移动到首位（#dummyNode之后）
  #moveToFirst(foundNode: Node) {
    const oldFirst = this.#dummyNode.next as Node;
    if (oldFirst === foundNode) return; // 已经顺序正确，不需要再移动

    oldFirst.prev = foundNode;
    this.#dummyNode.next = foundNode;
    foundNode.prev!.next = foundNode.next;
    foundNode.next!.prev = foundNode.prev;
    foundNode.prev = this.#dummyNode;
    foundNode.next = oldFirst;
  }

  constructor(capacity: number) {
    this.#capacity = capacity;
    this.#nodeMap = new Map();
    this.#dummyNode = new Node(-1, -1, null, null);
    this.#dummyNode.next = this.#dummyNode;
    this.#dummyNode.prev = this.#dummyNode;
  }

  get(key: number): number {
    const foundNode = this.#nodeMap.get(key);
    if (!foundNode) return -1;

    this.#moveToFirst(foundNode);

    return foundNode.val;
  }

  put(key: number, value: number): void {
    const foundNode = this.#nodeMap.get(key);
    if (foundNode) {
      // 更新节点
      foundNode.val = value;
      this.#moveToFirst(foundNode);

      return;
    }

    // 插入节点
    if (this.#capacity > 0) {
      // 未达到最大容量，插入节点
      this.#putInList(key, value);
      this.#capacity--;
    } else {
      // 已达到最大容量，插入、删除节点
      this.#putInList(key, value);
      const toDel = this.#dummyNode.prev as Node;
      this.#dummyNode.prev = toDel.prev;
      toDel.prev!.next = toDel.next;
      this.#nodeMap.delete(toDel.key);
    }
  }
}