[NOIP2023] 双序列拓展题解

知识点

Ad-hoc，贪心，动态规划。

题意简述

给定两个序列 \(X,Y\)，要求将两个序列中每个元素都替换成多个相同的元素，最终得到两个长为 \(10^{100}\) 的拓展序列 \(F = \{ f_i \},G = \{ g_i \}\)，满足 \(\forall i,j \in [1,10^{100}],(f_i - g_i)(f_j - g_j)>0\)。

现在给你多个 \(X,Y\)，一一判断他们是否能够构造出满足上述要求的序列 \(F,G\)。

分析

\(35\%\)

首先可以看出，题目中将扩充后的序列长度设为 \(10^{100}\) 就是能够让我们较为自由的拓展，其实就是个幌子。

再来看序列要求：\(\forall i,j \in [1,10^{100}],(f_i - g_i)(f_j - g_j)>0\)，有学过数学的人都知道：\(xy > 0\) 就是在说 \(x\) 与 \(y\) 的符号相同，\(xy < 0\) 则是符号不同。

那么代入上式，它的意思就是 \(\forall i \in [1,10^{100}],f_i > g_i\) 或 \(\forall i \in [1,10^{100}],f_i < g_i\)。

其实这两种条件都是等价的，只要把初始序列 \(X,Y\) 交换一下就一样了。我们考虑求解满足 \(\forall i \in [1,10^{100}],f_i < g_i\) 的序列条件。

我们有一种思路，可以往 \(F,G\) 中一个个加入 \(X,Y\) 中的元素，由于 \(10^{100}\) 长度足够长，所以我们只用考虑现在加入的一对元素 \((x_i,y_j),x_i \in X,y_j \in Y\)，是否满足条件，然后需要更换元素的时候可以让元素对变成 \((x_{i+1},y_j),(x_i,y_{j+1}),(x_{i+1},y_{j+1})\)，否则就会有落下的元素。那么我们可以设计一种二维可行性 DP：

设 \(f_{i,j}\) 表示 \((x_i,y_j)\) 是否能够作为一对一起加入的元素对。

那么我们的边界条件就为 \(f_{1,1} = [x_1 < y_1]\)，转移方程：（逻辑与 \(\land\)，逻辑或 \(\lor\)）

\[f_{i,j} = (f_{i-1,j}[i > 1] \lor f_{i,j-1}[j > 1] \lor f_{i-1,j-1}[i > 1 \land j > 1]) \land [x_i < y_j] \\ \]

最终 \(f_{n,m}\) 就是答案。

代码

时空复杂度：\(O(\frac{nm}{w})\)。

namespace Subtask1 {
	const int N(2e3+10);
	bitset<N> f[N];
	bool Check() {
		return ID<=7;
	}
	int Cmain(bool &ans) {
		FOR(i,1,n)FOR(j,1,m)f[i][j]=0;
		f[0][0]=1;
		FOR(i,1,n)FOR(j,1,m)if(a[i]<b[j]&&(f[i-1][j]==1||f[i][j-1]==1||f[i-1][j-1]==1))f[i][j]=1;
		ans=(f[n][m]==1);
		return 0;
	}
}

\(70\%\)

特殊性质：对于每组询问（包括初始询问和额外询问），保证 \(x_1 < y_1\)，且 \(x_n\) 是序列 \(X\) 唯一的一个最小值，\(y_m\) 是序列 \(Y\) 唯一的一个最大值。

我们重新审视一遍上面的暴力：二维，边界为 \(f_{1,1}\)，转移下标间只差 \(1\)，下标都不能减少。

这像一个路径计数问题，但是我们在这里记的是可行性，那么就又像一个二维网格图上 BFS 来找 \((1,1)\) 能到达的点。

没错！我们可以把它们转化成二维网格图上的可达性问题，而转化到这上面之后，问题似乎就变得清晰明了了。但是这和上面提到的特殊性质又有什么关系呢？

我们设 \(gre_{i,j} \gets [x_i < y_j]\)，那么转换到一个表格上之后，我们把 \(gre_{i,j}\) 值为 \(\operatorname{true}\) 的染红，为 \(\operatorname{false}\) 则染蓝，会得到一张性质非常好的图。

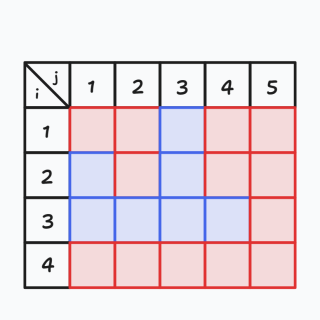
我们举个例子：\(X = {\{ 2,6,10,1 \}},Y = {\{ 3,9,2,8,15 \}}\)，这个例子满足特殊性质。那么会得到下图：

我们发现最后一行和最后一列一定是全部涂红的，那么我们思考：为什么会变成这样？因为特殊性质里说了：

\(x_n\) 是序列 \(X\) 唯一的一个最小值，\(y_m\) 是序列 \(Y\) 唯一的一个最大值。

那么导致了最后一行和最后一列一定是满足 \(x_i < y_j\) 的。那也就是说，只要我们能走到最后一行或最后一列的任意一个位置，也就一定能够走到终点。

可是我们该如何利用这个性质呢？

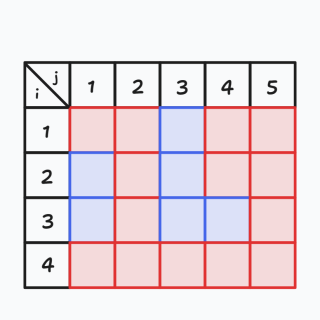
再举个例子，只改变上面 \(X\) 中的一位，\(X = {\{ 2,6,8,1 \}},Y = {\{ 3,9,2,8,15 \}}\)，那么表格变成了下图：

红色的方格形成了一条通路，我们把此时最后一行和最后一列用紫色标记出来，如下图：

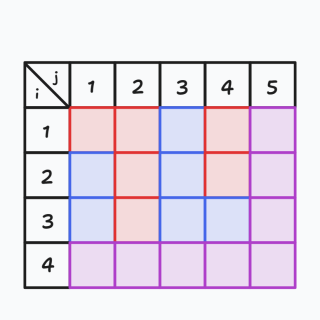
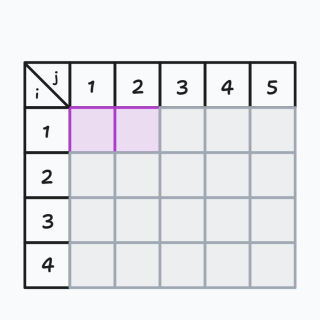
我们找到来到这里的路径，它是从 \((4,2)\) 这个点进入紫色范围的，我们仿照上面，把这时候的第 \(2\) 行给标成紫色，得到下图：

最后一步的我们同样也标记上，得到最后一幅图：

我们发现这三张图有一个共性，紫色对整张图中 \((x,y),x\le i,y \le j\) 的部分包围了起来，而且它们都满足：

\[x_i = \min_{a \le i} {\{ x_a \}},y_j = \max_{b \le j} {\{ y_b \}} \\ \]

这个性质使得它们就像一开始的最后一行和最后一列一样，一定都是可以通向最右下角的那个点的。

它们像是一个个包围圈，一步步地把范围缩小，那么我们是不是也可以仿照这种方式，一步步地找到范围之内 \(\min_{a \le i} {\{ x_a \}}\) 和 \(\max_{b \le j} {\{ y_b \}}\)，然后把右下角的坐标其中一个进行转移缩小，最后无法缩小时，就可以判断是否有解。

为什么说：“把右下角的坐标其中一个进行转移缩小，最后无法缩小时，就可以判断是否有解”，而不是要把所有情况都像 DFS 一样回溯判断一遍呢？

因为只要有解，选择其中一个回溯下去就一定能找到解，我们感性证明一下（不完全严谨的证明）：

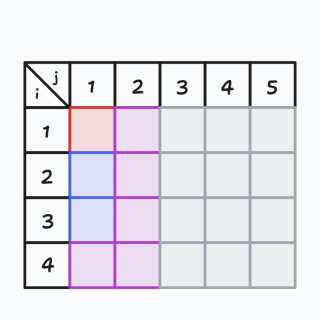
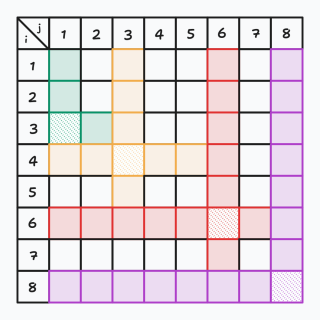
发现如果我们现在的边框（收缩后最后一行和最后一列）如果与 \((1,1)\) 连通，那么它就一定能够通过缩小某一维的坐标去连接到中间部分，完全不需要回溯，因为当 \((i,j)\) 满足 \(x_i = \min_{a \le i} {\{ x_a \}},y_j = \max_{b \le j} {\{ y_b \}}\) 的时候，它会直接连接到 \((i,1)\) 和 \((1,j)\)。如下图（阴影方格就是满足 \(x_i = \min_{a \le i} {\{ x_a \}},y_j = \max_{b \le j} {\{ y_b \}}\) 的 \((i,j)\)）。

换言之，我们的边框如果无法缩小，就代表中间没有与它连通的方格了，我们可以直接直接判为无解，就如下图一样。

那么我们根据这个性质，对于两个维度 \(X\) 和 \(Y\) 分别求出前缀最小值位置和前缀最大值位置，然后进行上述过程，直接用一次 DFS 即可。

代码

时空复杂度：\(O(n+m)\)。

struct node {
	int mi,mx;
	node(int mi=0,int mx=0):mi(mi),mx(mx) {}
} prea[N],preb[N];
node Merge(int *a,node A,node B) {
	return node(a[A.mi]<a[B.mi]?A.mi:B.mi,a[A.mx]>a[B.mx]?A.mx:B.mx);
}
namespace Subtask2 {
	bool Check() {
		return ID<=14;
	}
	bool dfs(int x,int y) {
		if(x==1||y==1)return 1;
		if(a[prea[x-1].mi]<b[preb[y-1].mi])return dfs(prea[x-1].mi,y);
		if(a[prea[x-1].mx]<b[preb[y-1].mx])return dfs(x,preb[y-1].mx);
		return 0;
	}
	int Cmain(bool &ans) {
		FOR(i,1,n)prea[i]=(i<=1?node(1,1):Merge(a,node(i,i),prea[i-1]));
		FOR(i,1,m)preb[i]=(i<=1?node(1,1):Merge(b,node(i,i),preb[i-1]));
		if(a[prea[n].mi]>=b[preb[m].mi]||a[prea[n].mx]>=b[preb[m].mx])return ans=0,0;
		return ans=dfs(n,m),0;
	}
}

\(100\%\)

如果你和我一样是用上述 \(70\%\) 的思路：把序列转化成二维表格来求解。那么现在这个正解，只要把脑筋转过来就肯定能想到了！

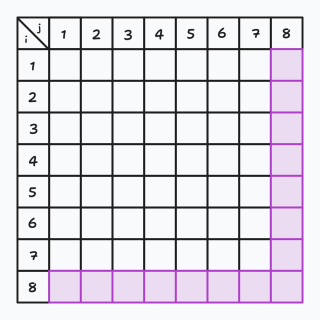
比如，上面的特殊性质使得二维表格长成这个样子：（空白的部分颜色任意）

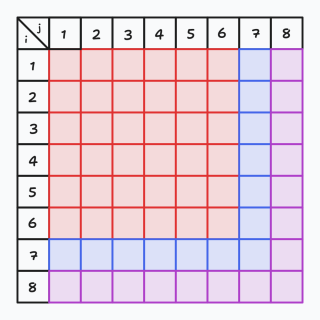
那么没有了特殊性质的二维表格就会长成这个样子：

又或是下面这样：

那么就非常简单了，我们把一张二维表格沿着一个其中紫色十字拆开，前半部分做一遍 \(70\%\) 部分分的验证，后半部分再做一遍 \(70\%\) 部分分的验证即可。

具体实现的话，我们可以分别处理出 \(X\) 的前、后缀最小值位置、\(Y\) 的前、后缀最大值位置，分别正着和反着来一遍 \(70\%\) 的验证过程。

代码

时空复杂度：\(O(n+m)\)。

struct node {
	int mi,mx;
	node(int mi=0,int mx=0):mi(mi),mx(mx) {}
} prea[N],preb[N],sufa[N],sufb[N];
node Merge(int *a,node A,node B) {
	return node(a[A.mi]<a[B.mi]?A.mi:B.mi,a[A.mx]>a[B.mx]?A.mx:B.mx);
}
namespace Subtask {
	template<const int sign>bool dfs(node *prea,node *preb,int x,int y,const int X,const int Y) {
		if(x==X||y==Y)return 1;
		if(a[prea[x+sign].mi]<b[preb[y+sign].mi])return dfs<sign>(prea,preb,prea[x+sign].mi,y,X,Y);
		if(a[prea[x+sign].mx]<b[preb[y+sign].mx])return dfs<sign>(prea,preb,x,preb[y+sign].mx,X,Y);
		return 0;
	}
	int Cmain(bool &ans) {
		FOR(i,1,n)prea[i]=(i<=1?node(1,1):Merge(a,node(i,i),prea[i-1]));
		FOR(i,1,m)preb[i]=(i<=1?node(1,1):Merge(b,node(i,i),preb[i-1]));
		DOR(i,n,1)sufa[i]=(i>=n?node(n,n):Merge(a,node(i,i),sufa[i+1]));
		DOR(i,m,1)sufb[i]=(i>=m?node(m,m):Merge(b,node(i,i),sufb[i+1]));
		if(a[prea[n].mi]>=b[preb[m].mi]||a[prea[n].mx]>=b[preb[m].mx])return ans=0,0;
		ans=dfs<-1>(prea,preb,prea[n].mi,preb[m].mx,1,1)&&dfs<1>(sufa,sufb,prea[n].mi,preb[m].mx,n,m);
		return 0;
	}
}

完整代码

#define Plus_Cat "expand"
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define ll long long
#define RCL(a,b,c,d) memset(a,b,sizeof(c)*(d))
#define tomin(a,...) ((a)=min({(a),__VA_ARGS__}))
#define tomax(a,...) ((a)=max({(a),__VA_ARGS__}))
#define FOR(i,a,b) for(int i(a); i<=(int)(b); ++i)
#define DOR(i,a,b) for(int i(a); i>=(int)(b); --i)
#define EDGE(g,i,x,y) for(int i(g.h[x]),y(g[i].v); ~i; y=g[i=g[i].nxt].v)
using namespace std;
namespace IOstream {
#define getc() getchar()
#define putc(ch) putchar(ch)
#define isdigit(ch) ('0'<=(ch)&&(ch)<='9')
	template<class T>void rd(T &x) {
		static char ch(0);
		for(x=0,ch=getc(); !isdigit(ch); ch=getc());
		for(; isdigit(ch); x=(x<<1)+(x<<3)+(ch^48),ch=getc());
	}
} using namespace IOstream;
constexpr int N(5e5+10),CAS(60+10);
bool ans[CAS];
int ID,_n,_m,n,m,Cas;
int _a[N],_b[N],a[N],b[N];
namespace Subtask1 {
	const int N(2e3+10);
	bitset<N> f[N];
	bool Check() {
		return ID<=7;
	}
	int Cmain(bool &ans) {
		FOR(i,1,n)FOR(j,1,m)f[i][j]=0;
		f[0][0]=1;
		FOR(i,1,n)FOR(j,1,m)if(a[i]<b[j]&&(f[i-1][j]==1||f[i][j-1]==1||f[i-1][j-1]==1))f[i][j]=1;
		ans=(f[n][m]==1);
		return 0;
	}
}
struct node {
	int mi,mx;
	node(int mi=0,int mx=0):mi(mi),mx(mx) {}
} prea[N],preb[N],sufa[N],sufb[N];
node Merge(int *a,node A,node B) {
	return node(a[A.mi]<a[B.mi]?A.mi:B.mi,a[A.mx]>a[B.mx]?A.mx:B.mx);
}
namespace Subtask2 {
	bool Check() {
		return ID<=14;
	}
	bool dfs(int x,int y) {
		if(x==1||y==1)return 1;
		if(a[prea[x-1].mi]<b[preb[y-1].mi])return dfs(prea[x-1].mi,y);
		if(a[prea[x-1].mx]<b[preb[y-1].mx])return dfs(x,preb[y-1].mx);
		return 0;
	}
	int Cmain(bool &ans) {
		FOR(i,1,n)prea[i]=(i<=1?node(1,1):Merge(a,node(i,i),prea[i-1]));
		FOR(i,1,m)preb[i]=(i<=1?node(1,1):Merge(b,node(i,i),preb[i-1]));
		if(a[prea[n].mi]>=b[preb[m].mi]||a[prea[n].mx]>=b[preb[m].mx])return ans=0,0;
		return ans=dfs(n,m),0;
	}
}
namespace Subtask {
	template<const int sign>bool dfs(node *prea,node *preb,int x,int y,const int X,const int Y) {
		if(x==X||y==Y)return 1;
		if(a[prea[x+sign].mi]<b[preb[y+sign].mi])return dfs<sign>(prea,preb,prea[x+sign].mi,y,X,Y);
		if(a[prea[x+sign].mx]<b[preb[y+sign].mx])return dfs<sign>(prea,preb,x,preb[y+sign].mx,X,Y);
		return 0;
	}
	int Cmain(bool &ans) {
		FOR(i,1,n)prea[i]=(i<=1?node(1,1):Merge(a,node(i,i),prea[i-1]));
		FOR(i,1,m)preb[i]=(i<=1?node(1,1):Merge(b,node(i,i),preb[i-1]));
		DOR(i,n,1)sufa[i]=(i>=n?node(n,n):Merge(a,node(i,i),sufa[i+1]));
		DOR(i,m,1)sufb[i]=(i>=m?node(m,m):Merge(b,node(i,i),sufb[i+1]));
		if(a[prea[n].mi]>=b[preb[m].mi]||a[prea[n].mx]>=b[preb[m].mx])return ans=0,0;
		ans=dfs<-1>(prea,preb,prea[n].mi,preb[m].mx,1,1)&&dfs<1>(sufa,sufb,prea[n].mi,preb[m].mx,n,m);
		return 0;
	}
}
int Cmain(bool &ans) {
	if(a[1]==b[1]||a[n]==b[m]||((a[1]<b[1])^(a[n]<b[m])))return ans=0,0;
	if(a[1]>b[1]) {
		swap(n,m);
		FOR(i,1,max(n,m))swap(a[i],b[i]);
	}
	if(Subtask1::Check())return Subtask1::Cmain(ans);
	if(Subtask2::Check())return Subtask2::Cmain(ans);
	return Subtask::Cmain(ans);
}
int main() {
#ifdef Plus_Cat
	freopen(Plus_Cat ".in","r",stdin),freopen(Plus_Cat ".out","w",stdout);
#endif
	rd(ID),rd(_n),rd(_m),rd(Cas);
	FOR(i,1,_n)rd(_a[i]),a[i]=_a[i];
	FOR(i,1,_m)rd(_b[i]),b[i]=_b[i];
	n=_n,m=_m,Cmain(ans[0]);
	FOR(i,1,Cas) {
		n=_n,m=_m;
		FOR(j,1,n)a[j]=_a[j];
		FOR(j,1,m)b[j]=_b[j];
		int Kx,Ky;
		rd(Kx),rd(Ky);
		while(Kx--) {
			int p,v;
			rd(p),rd(v),a[p]=v;
		}
		while(Ky--) {
			int p,v;
			rd(p),rd(v),b[p]=v;
		}
		Cmain(ans[i]);
	}
	FOR(i,0,Cas)putchar(ans[i]|'0');
	puts("");
	return 0;
}

反思

优点

没有思路时果断放弃，选择只打了部分分。

缺点

部分分想了挺久的，脑子转的太慢了。
打出部分分后还没有意识到可以转换到二维网格图中，还没有养成把模型转换成图论的习惯。

posted @ 2024-11-22 21:28 Add_Catalyst 阅读(21) 评论(0) 收藏举报

刷新页面返回顶部

珈猫的小窝

欢迎来到珈猫的小窝

[NOIP2023] 双序列拓展题解

[NOIP2023] 双序列拓展题解

知识点

题意简述

分析

\(35\%\)

代码

\(70\%\)

代码

\(100\%\)

代码

完整代码

反思

优点

缺点

公告

珈猫的小窝

欢迎来到珈猫的小窝

[NOIP2023] 双序列拓展 题解

[NOIP2023] 双序列拓展 题解

知识点

题意简述

分析

\(35\%\)

代码

\(70\%\)

代码

\(100\%\)

代码

完整代码

反思

优点

缺点

公告

[NOIP2023] 双序列拓展题解

[NOIP2023] 双序列拓展题解