[NOIP2022] 喵了个喵 题解
[NOIP2022] 喵了个喵 题解
知识点
贪心,构造,模拟。
题意简述
本题有多组询问。
有 \(n\) 个栈,一个包含 \(m\) 张牌的牌堆,这些牌有 \(k \in \{2n - 2,2n - 1\}\) 种。
现在可进行如下操作:
- 取出牌堆顶的牌,放入某个栈。如果原栈顶牌种类与它相同,则两张牌消除。
- 选取两个栈,如果它们栈底的牌种类相同,则这两张牌抵消。
问一种方案,总操作次数在 \([m,2m]\) 内,使得所有牌都会被消除。
分析
\(k = 2n - 2\)
首先我们考虑这个部分分,有一定数感的人都可以看出来:\(k = 2(n-1)\),那么我们把 \(k\) 种两两分组,分成 \(n-1\) 组,每组分配一个栈,最后会剩下一个空栈。
现在方案就非常明了了:取出牌,分类讨论。
\(k = 2n - 1\)
我们发现这个似乎直接想并不好想,尝试把上面 \(k = 2n - 2\) 时的方法也套入,也就是多出来一个单独放。
但是我们如果像上面一样直接分组固定了,也不太可行,那么我们可以考虑动态维护分组,也就是先加进来的种类两两一组,按照上面的方法处理,最后剩下的没加的种类在加入时直接一次性和后面的一些牌一起处理掉,不让处理以外时已经加入的种类总数超过 \(2n-2\)。
这样就可以保证处理以外时始终有一个空栈和没加入的种类,同时保证了有解的可能性。
那么我们考虑一次性处理的方案:我们把牌堆顶上的牌逐个取出进行处理,发现如果这个种类是在某个栈顶,那么影响其实不大,真正需要考虑的其实是在栈底的那些种类或是与它相同的种类。
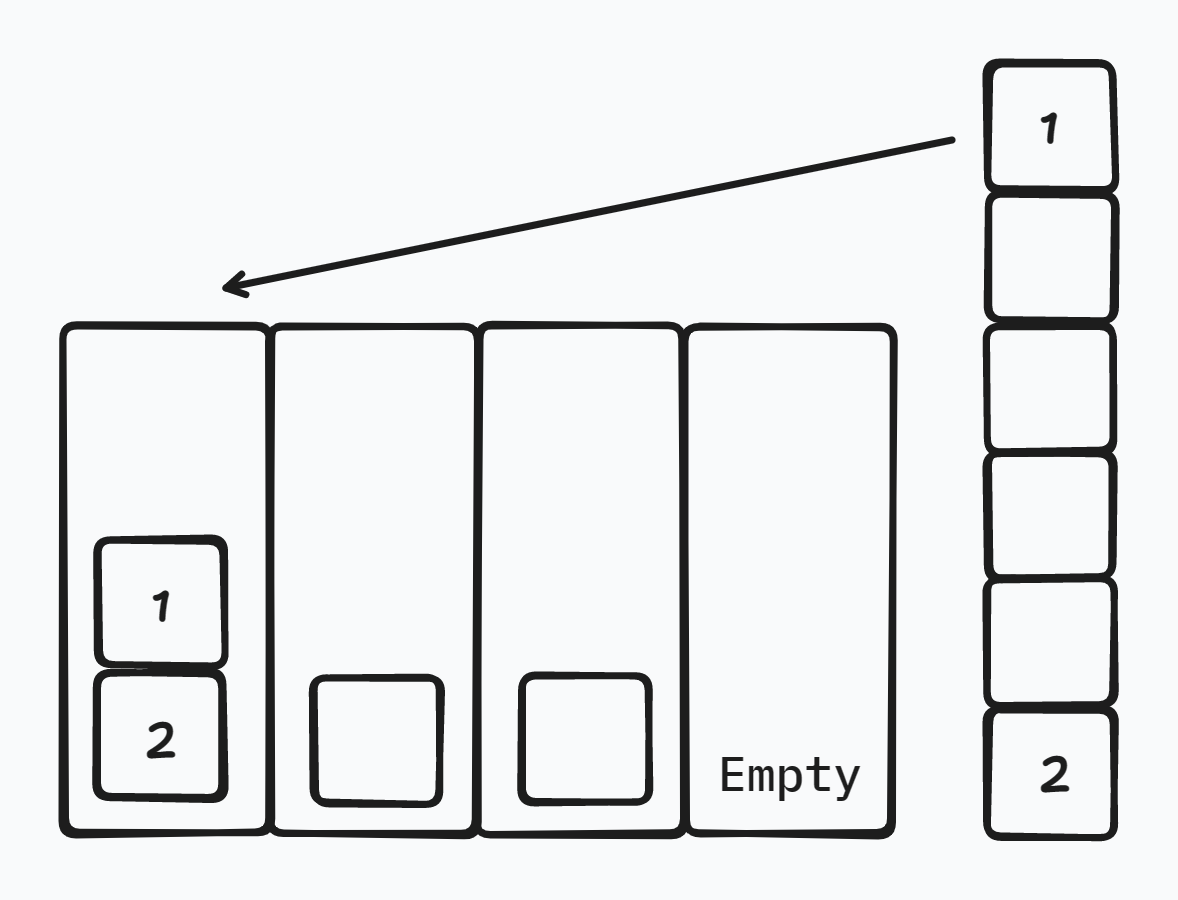
现在多出来的种类设为 \(x\),在原牌堆位置中位置为 \(i\),它的下一张不在某个栈顶的牌种类设为 \(y\),位于 \(j\)。
(解释顺序与实操顺序不一致,请注意。)
-
\(x = y\):
直接把这两张牌都放在空栈中抵消,剩下中间位于原牌堆 \([i+1,j-1]\) 部分(如果有,即 \(j-i>1\))的会直接与对应的牌堆顶抵消,不会用到空栈,那么就是合法的。
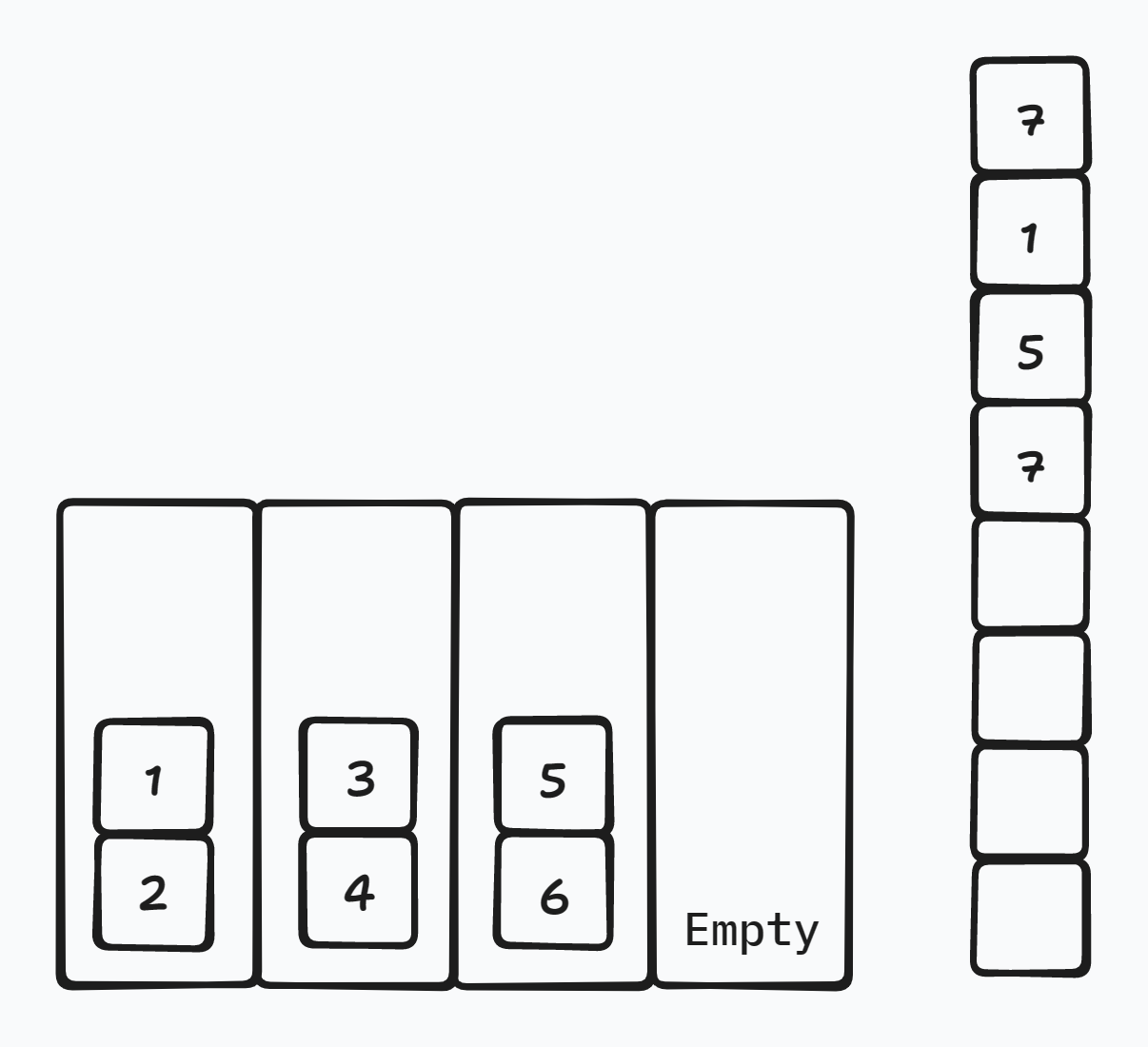
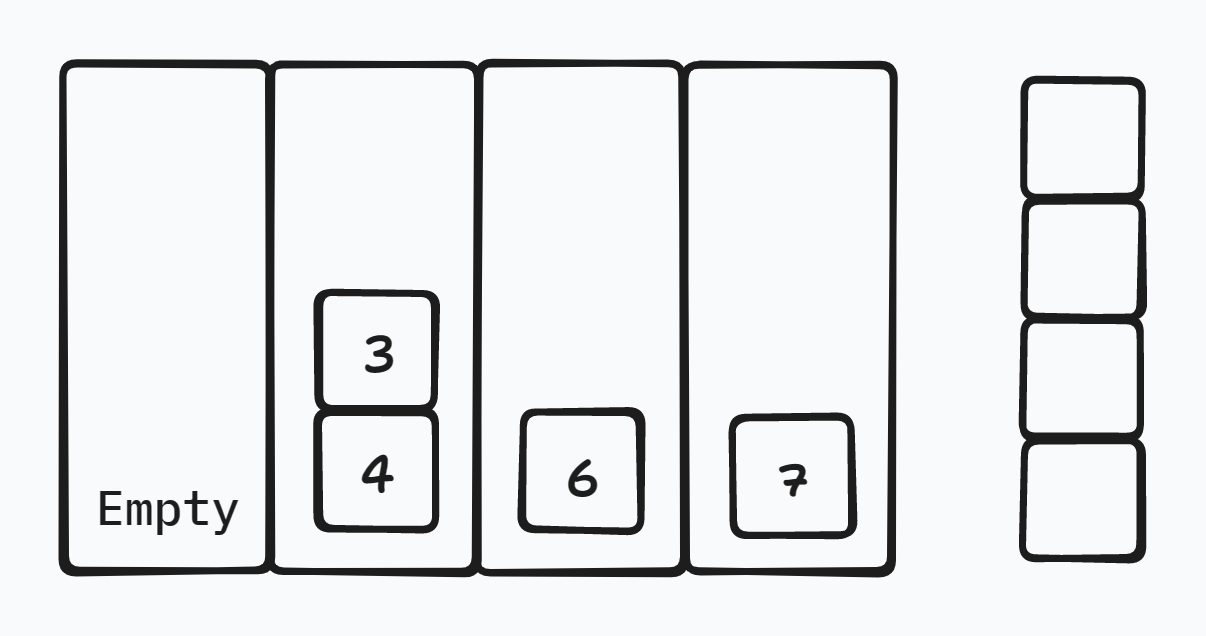
图示中,\(x = y = 7\),它们可以先后放到空栈中,其余的种类会在自己种类的栈顶上抵消掉。
-
\(x \neq y\):
先来看一个示例:
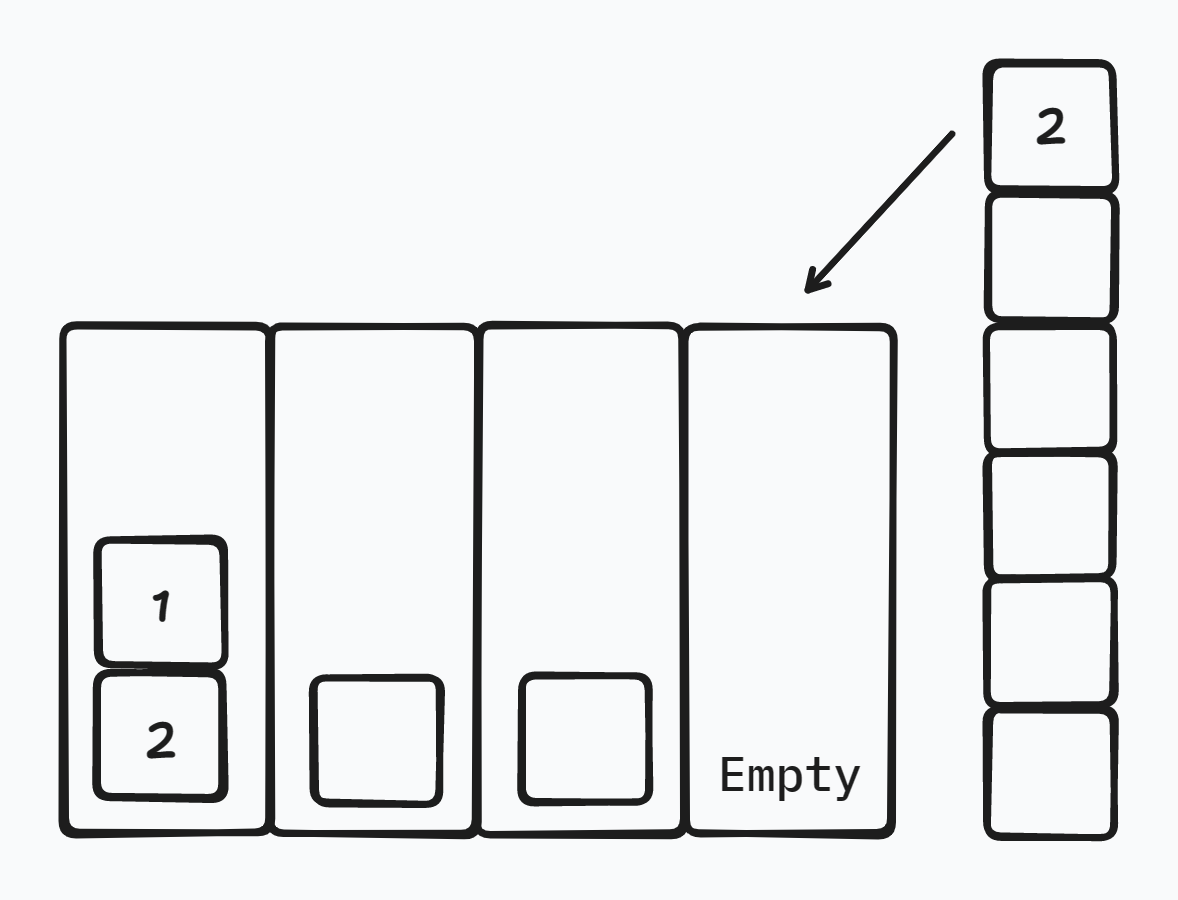
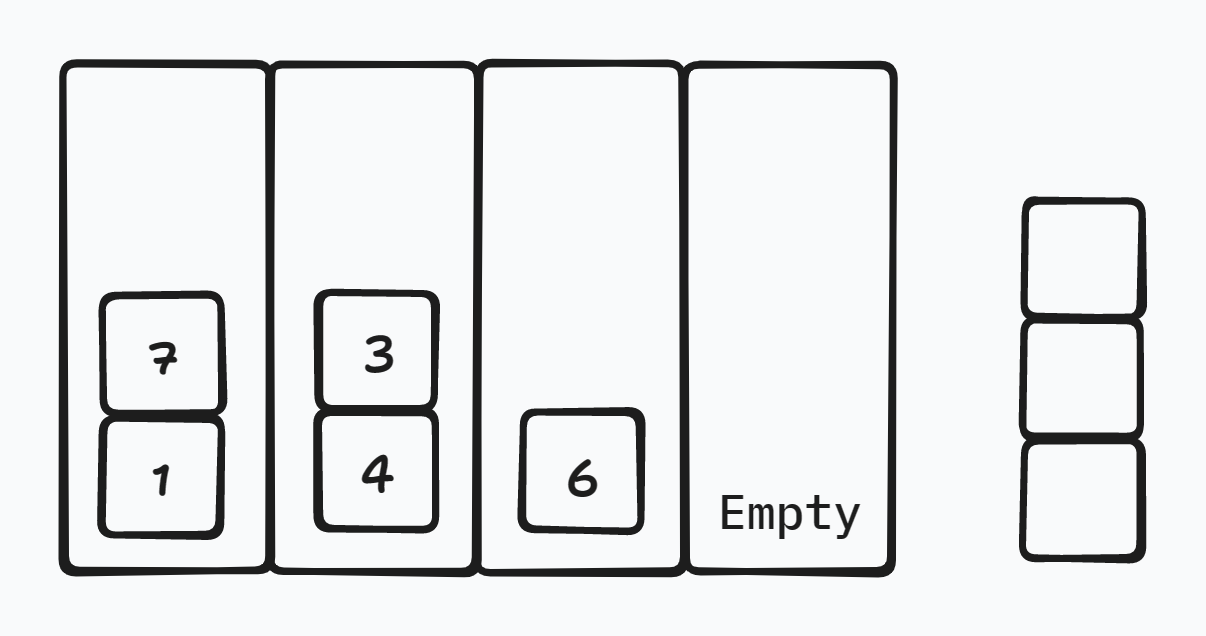
其中 \(x=7,y=2\),我们是不是可以像之前所有的策略一样直接把这个 \(7\) 扔到空栈中去呢?显然地,可以。
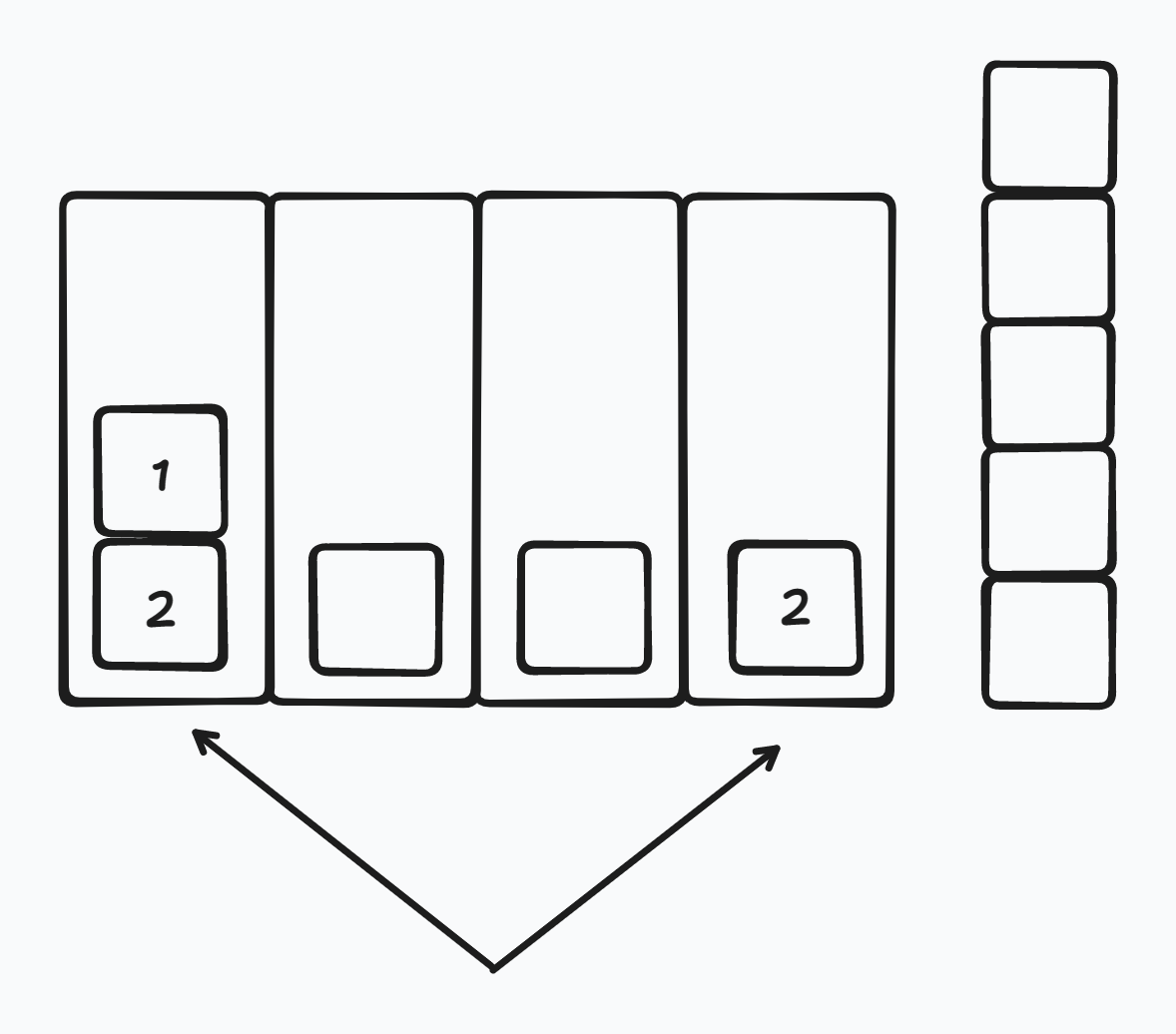
那这能够说明我们遇到所有多出来的种类都可以直接扔到空栈中吗?我们很容易就能举出反例,如下:
我们发现只是牌堆内多了一个 \(1\),上面的方法就行不通了。那为什么呢?原因很简单:
- 当 \([i+1,j-1]\) 中(如果存在,即 \(j-i>1\))有奇数个 \(1\),它们连通栈顶的 \(1\) 会正好两两抵消,最后栈顶会空出来,可以让牌堆中的 \(2\) 直接与栈中的 \(2\) 抵消。
- 但是当这其中只有偶数个时,它们不会两两抵消,会正好多出来一个,留在栈顶,阻挡了牌堆中的 \(2\) 与栈中的 \(2\) 抵消。
我们该如何处理这种情况呢?其实只需要稍微转换一下:
- 由于 \(2\) 位于栈底,上面的 \(1\) 在最坏情况下是不会消除的,所以空栈最后一定是要留出来给 \(2\) 进行抵消的。
- 而除了这个栈,其他非空栈栈顶可能都需要用来抵消,也不能占用,那么 \(7\) 只能放在空栈或 \(2\) 的栈顶,又因为空栈最终是需要留出来给 \(2\) 的,那么它只能放在 \(2\) 的栈顶。
- 同时,栈中的 \(1\) 可以很巧妙的放在空栈中一一抵消,最终变空。
最终我们会得到方案:
设位于 \(y\) 栈顶的元素为 \(z\)。
-
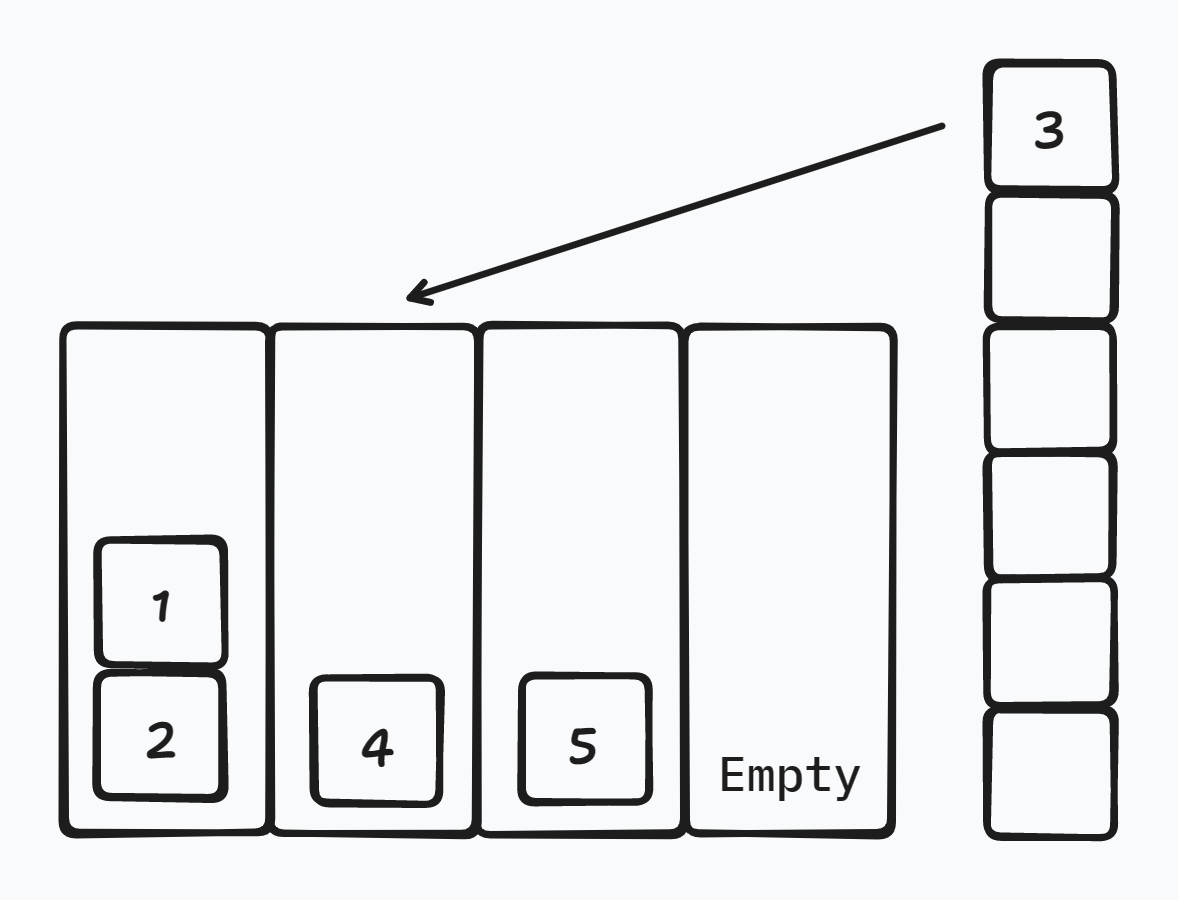
当 \([i+1,j-1]\) 中(如果存在,即 \(j-i>1\))有奇数个 \(z\):
那么将 \(x\) 放入空栈中,剩下的都让它们放到各自的栈中,所有都可以直接抵消。
要注意的是:这样操作后,空栈位置会变。
示例:
处理前:
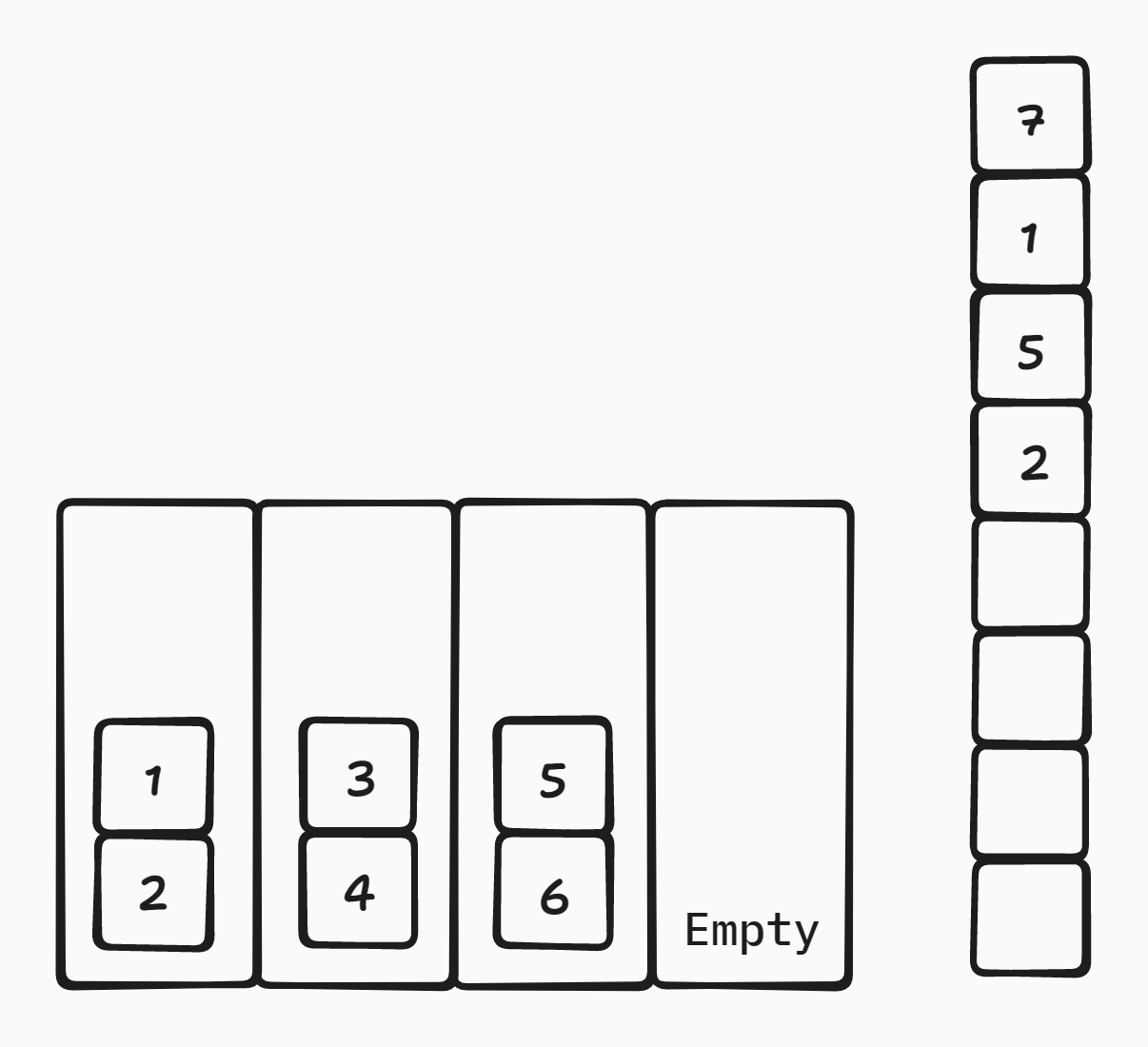
处理后:
-
当 \([i+1,j-1]\) 中(如果存在,即 \(j-i>1\))有偶数个 \(z\):
将 \(x\) 放到 \(y\) 栈顶。然后遍历 \([i+1,j-1]\) 中的元素,如果是 \(z\),那么都放到空栈中;否则直接加入原栈抵消。最后把 \(y\) 加入空栈和原本 \(y\) 在的栈进行栈底相消。
要注意的是:这样操作后,\(x\) 会变成栈顶,\(z\) 会变成栈底。
示例:
处理前:
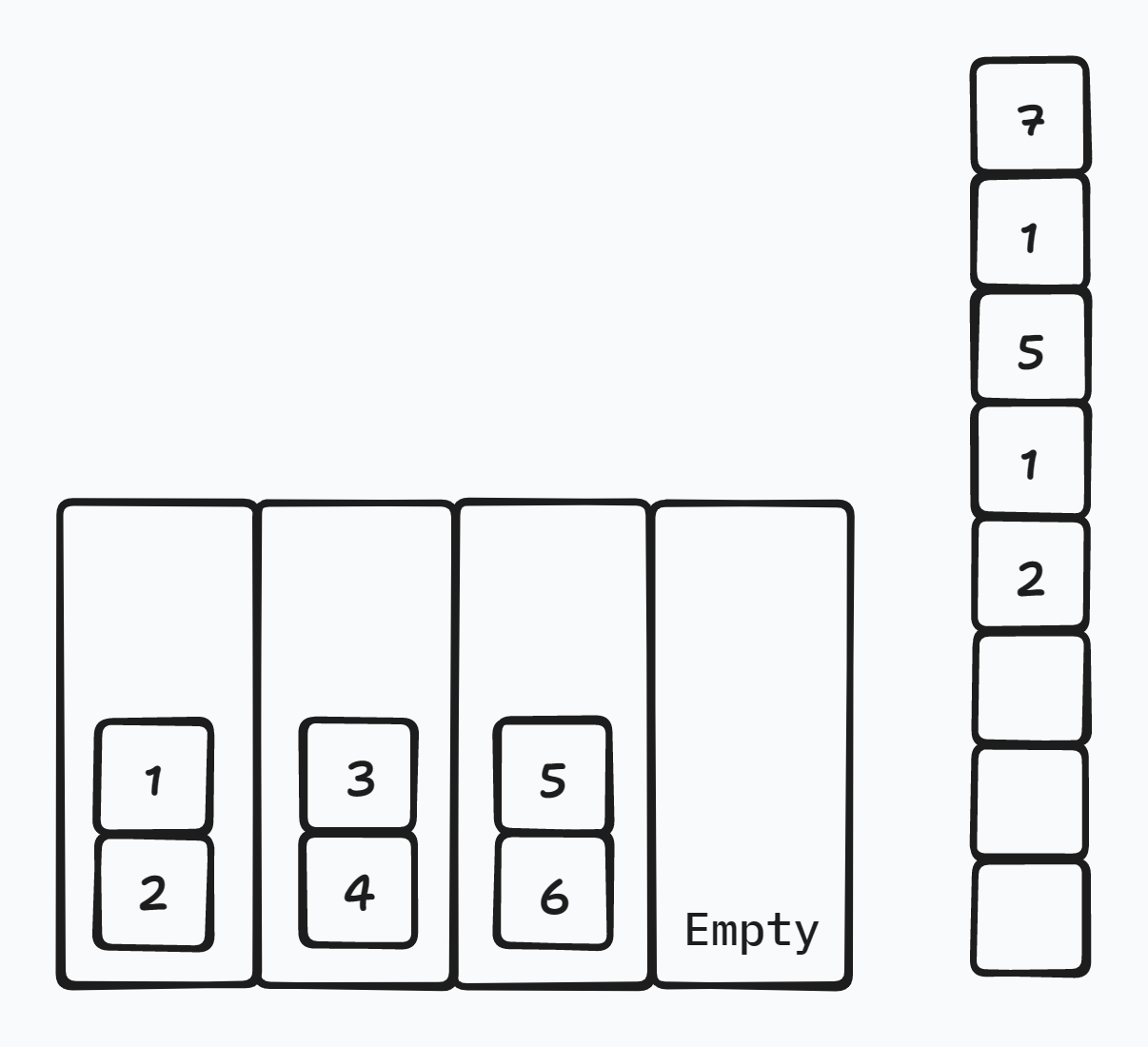
处理后:
实现
分析是一回事,实现又是另一回事。如何快速实现这题的程序又是一个较大的问题。
动态维护所有栈
维护每个种类牌所在位置
开一个 \(pos\) 数组,\(pos_i\) 表示 \(i\) 所在位置信息:
- \(pos_i = 0\),那么 \(i\) 不在任何一个栈中;
- \(pos_i<0\),那么 \(i\) 在第 \(|pos_i|\) 个栈的栈底;
- \(pos_i>0\),那么 \(i\) 在第 \(|pos_i|\) 个栈的栈顶。
维护空栈与只有单个元素的栈编号
如何动态维护栈是否空余就是一个非常大的难点。
我在这里采用了 std::list<int>,保证在这里面最后一个存的是空栈编号,前面存大小 \(\le 1\) 的栈,并且编号不重复。
由于不好整体更新,我们就不维护“前面存大小 \(\le 1\) 的栈,并且编号不重复”这两个条件,直接在需要用到时把前面不符合条件的取出即可。
但是“最后一个存的是空栈编号”这个条件很重要,是一定要维护的,而且维护也相对简单。
维护栈内情况
为了方便,我们也可以开一个自己的结构体栈,顺便把栈底相消的函数也写出来:
因为栈的大小最大不超过 \(3\),我们直接暴力修改即可。
struct Desta {
int n,idx;
int a[4];
bool empty() {
return !n;
}
int size() {
return n;
}
int bot() {
return a[1];
}
int top() {
return a[n];
}
void clear() {
n=0;
}
void push(int x) {
Ans[++Top]=Operation(1,idx),n&&a[n]==x?--n:a[++n]=x;
}
void pop_top() {
--n;
}
void pop_bot() {
--n;
if(n>0)a[1]=a[2];
if(n>1)a[2]=a[3];
}
} ds[N];
bool Operate(Desta &A,Desta &B) {
if(A.bot()!=B.bot())return 0;
return Ans[++Top]=Operation(2,A.idx,B.idx),A.pop_bot(),B.pop_bot(),1;
}
取牌操作
\(2n - 2\) 操作
首先,这个操作作为整题分析的基础,我们可以单独写成一个 bool 类的函数,以便接下来操作方便判断和调用:
bool Push(int x) {
if(pos[x]) {
if(pos[x]>0)ds[pos[x]].push(x),Emp.push_front(pos[x]);
else {
if(ds[-pos[x]].size()>1) {
ds[Emp.back()].push(x),Operate(ds[Emp.back()],ds[-pos[x]]);
pos[ds[-pos[x]].bot()]=pos[x],Emp.push_front(-pos[x]);
} else ds[-pos[x]].push(x);
}
return pos[x]=0,1;
} //原本有栈中有这种牌
while((int)Emp.size()>1&&(ds[Emp.front()].size()>1||Emp.front()==Emp.back()))Emp.pop_front(); //取出 std::list<int> Emp 中不符条件的作为 front() 的值
if((int)Emp.size()>1) {
pos[x]=ds[Emp.front()].empty()?-Emp.front():Emp.front(),ds[Emp.front()].push(x);
if(ds[Emp.front()].size()>1)Emp.pop_front();
return 1;
} //原本没有栈中有这种牌
return 0; //牌种类到达 2n-2,不能再直接加入
}
Push(x) 表示把牌堆中种类为 \(x\) 的牌取出加入栈中,如果能直接按照 \(k = 2n - 2\) 时的操作来,则返回 true,否则返回 false.
一次性处理
剩下的都不难处理:
int j(i+1);
while(j<=m&&pos[a[j]]>0)++j;
if(a[i]==a[j]) {
ds[Emp.back()].push(a[i]);
while(++i<j)Push(a[i]);
ds[Emp.back()].push(a[i]);
continue;
} //x = y
bool flag(0);
int idx(-pos[a[j]]),top(ds[idx].top());
FOR(k,i+1,j-1)flag^=(a[k]==top);
if(flag) {
ds[Emp.back()].push(a[i]),pos[a[i]]=-Emp.back();
while(++i<j)a[i]==top?ds[idx].push(a[i]),1:Push(a[i]);
pos[top]=0,ds[idx].push(a[i]),pos[a[i]]=0,Emp.push_back(idx);
continue;
} //[i+1,j-1] 中有奇数个 z
pos[ds[idx].top()]=0,ds[pos[a[i]]=idx].push(a[i]);
while(++i<j)a[i]==top?ds[Emp.back()].push(a[i]),1:Push(a[i]);
ds[Emp.back()].push(a[i]),pos[a[i]]=0,Operate(ds[idx],ds[Emp.back()]),pos[ds[idx].bot()]=-idx; //[i+1,j-1] 中有偶数个 z
代码
时空复杂度:\(O(\sum(n+m+k))\)。
#define Plus_Cat "meow"
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define ll long long
#define RCL(a,b,c,d) memset(a,b,sizeof(c)*(d))
#define FOR(i,a,b) for(int i(a);i<=(int)(b);++i)
#define DOR(i,a,b) for(int i(a);i>=(int)(b);--i)
#define tomin(a,...) ((a)=min({(a),__VA_ARGS__}))
#define tomax(a,...) ((a)=max({(a),__VA_ARGS__}))
#define EDGE(g,i,x,y) for(int i((g).h[x]),y((g)[i].v);~i;y=(g)[i=(g)[i].nxt].v)
using namespace std;
namespace IOstream {
#define getc() getchar()
#define putc(c) putchar(c)
#define isdigit(c) ('0'<=(c)&&(c)<='9')
template<class T>void rd(T &x) {
static char ch(0);
for(x=0,ch=getc();!isdigit(ch);ch=getc());
for(;isdigit(ch);x=(x<<1)+(x<<3)+(ch^48),ch=getc());
}
template<class T>void wr(T x,const char End='\n') {
static int top(0);
static int st[50];
do st[++top]=x%10,x/=10;
while(x);
while(top)putc(st[top]^48),--top;
putc(End);
}
} using namespace IOstream;
constexpr int N(3e2+10),K(6e2+10),M(2e6+10);
int Cas,n,m,k,Top;
int a[M],pos[K];
list<int> Emp;
struct Operation {
int type,s1,s2;
Operation(int type=0,int s1=0,int s2=0):type(type),s1(s1),s2(s2) {}
void Print() {
wr(type,' '),type==1?wr(s1):(wr(s1,' '),wr(s2));
}
} Ans[M<<1];
struct Desta {
int n,idx;
int a[4];
bool empty() {
return !n;
}
int size() {
return n;
}
int bot() {
return a[1];
}
int top() {
return a[n];
}
void clear() {
n=0;
}
void push(int x) {
Ans[++Top]=Operation(1,idx),n&&a[n]==x?--n:a[++n]=x;
}
void pop_top() {
--n;
}
void pop_bot() {
--n;
if(n>0)a[1]=a[2];
if(n>1)a[2]=a[3];
}
} ds[N];
bool Operate(Desta &A,Desta &B) {
if(A.bot()!=B.bot())return 0;
return Ans[++Top]=Operation(2,A.idx,B.idx),A.pop_bot(),B.pop_bot(),1;
}
bool Push(int x) {
if(pos[x]) {
if(pos[x]>0)ds[pos[x]].push(x),Emp.push_front(pos[x]);
else {
if(ds[-pos[x]].size()>1) {
ds[Emp.back()].push(x),Operate(ds[Emp.back()],ds[-pos[x]]);
pos[ds[-pos[x]].bot()]=pos[x],Emp.push_front(-pos[x]);
} else ds[-pos[x]].push(x);
}
return pos[x]=0,1;
}
while((int)Emp.size()>1&&(ds[Emp.front()].size()>1||Emp.front()==Emp.back()))Emp.pop_front();
if((int)Emp.size()>1) {
pos[x]=ds[Emp.front()].empty()?-Emp.front():Emp.front(),ds[Emp.front()].push(x);
if(ds[Emp.front()].size()>1)Emp.pop_front();
return 1;
}
return 0;
}
int Cmain() {
/*Scan*/
rd(n),rd(m),rd(k);
FOR(i,1,m)rd(a[i]);
/*Init*/
FOR(i,1,n)Emp.push_back(i);
/*Solve*/
FOR(i,1,m) {
if(Push(a[i]))continue;
int j(i+1);
while(j<=m&&pos[a[j]]>0)++j;
if(a[i]==a[j]) {
ds[Emp.back()].push(a[i]);
while(++i<j)Push(a[i]);
ds[Emp.back()].push(a[i]);
continue;
}
bool flag(0);
int idx(-pos[a[j]]),top(ds[idx].top());
FOR(k,i+1,j-1)flag^=(a[k]==top);
if(flag) {
ds[Emp.back()].push(a[i]),pos[a[i]]=-Emp.back();
while(++i<j)a[i]==top?ds[idx].push(a[i]),1:Push(a[i]);
pos[top]=0,ds[idx].push(a[i]),pos[a[i]]=0,Emp.push_back(idx);
continue;
}
pos[ds[idx].top()]=0,ds[pos[a[i]]=idx].push(a[i]);
while(++i<j)a[i]==top?ds[Emp.back()].push(a[i]),1:Push(a[i]);
ds[Emp.back()].push(a[i]),pos[a[i]]=0,Operate(ds[idx],ds[Emp.back()]),pos[ds[idx].bot()]=-idx;
}
/*Print*/
wr(Top);
FOR(i,1,Top)Ans[i].Print();
/*Clear*/
Top=0,RCL(pos+1,0,int,k),Emp.clear();
FOR(i,1,n)ds[i].clear();
return 0;
}
int main() {
#ifdef Plus_Cat
freopen(Plus_Cat ".in","r",stdin),freopen(Plus_Cat ".out","w",stdout);
#endif
FOR(i,1,N-5)ds[i].idx=i;
for(rd(Cas); Cas; --Cas)Cmain();
return 0;
}