Educational Codeforces Round 68 (Rated for Div. 2) B. Yet Another Crosses Problem

Educational Codeforces Round 68 (Rated for Div. 2)

翻译 岛田小雅

B. Yet Another Crosses Problem

出题人 MikeMirzayanov

给你一个 \(n\) 行 \(m\) 列的矩阵，行的编号从上到下分别为 \(1\) 到 \(n\) ，列的编号从左到右分别为 \(1\) 到 \(m\)。每个格子都被涂成黑色或白色。

你觉得这个矩阵看起来还不够有趣，如果有至少一个十字在里面就好了。一个十字由一对数字 \(x\) 和 \(y\) 表示，其中 \(1≤x≤n\)，\(1≤y≤m\)，所有在第 \(x\) 行和第 \(y\) 列的方块都是黑色的。

比如，下面这些情况都属于有十字：

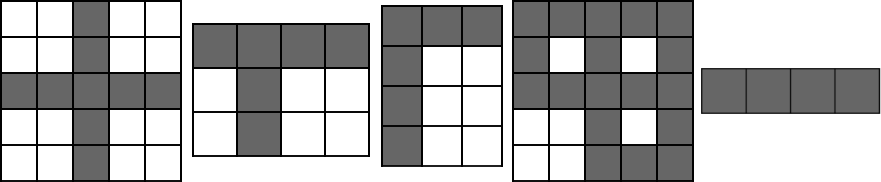
第四张图有 \(4\) 个十字，分别在 \((1,3), (1,5), (3,3)\) 和 \((3,5)\)。

下面的图不含有十字：

你有一把刷子和一桶黑色油漆，你可以让这幅画变得有趣。每涂黑一个格子将消耗你一分钟时间。

那么你最短需要几分钟才能让矩阵含有至少一个十字呢？

你需要回答多个独立的问题。

输入格式

第一行是整型 \(q\) \((1≤q≤5⋅10^4)\) ，代表测试点个数。

每个测试点的第一行有两个数 \(n\) 和 \(m\) \((1≤n,m≤5⋅10^4, n⋅m≤4⋅10^5)\)，分别表示矩阵的行数和列数。

下面 \(n\) 行每行有 \(m\) 个字符，‘\(.\)’ 代表这个格子是白色，而 ‘\(*\)’ 代表颜色是黑色。

数据保证 \(∑n≤5⋅10^4\) 且 \(∑n⋅m≤4⋅10^5\)。

输出格式

输出 \(q\) 行，第 \(i\) 行输出一个整型作为第 \(i\) 个测试点的答案，即使矩阵含有至少一个十字的最短时间（分钟）。

样例

输入

9
5 5
..*..
..*..
*****
..*..
..*..
3 4
****
.*..
.*..
4 3
***
*..
*..
*..
5 5
*****
*.*.*
*****
..*.*
..***
1 4
****
5 5
.....
..*..
.***.
..*..
.....
5 3
...
.*.
.*.
***
.*.
3 3
.*.
*.*
.*.
4 4
*.**
....
*.**
*.**

输出

0
0
0
0
0
4
1
1
2

补充

样例按照顺序包含了上面所有的图片。

前五张图里已经存在了一个十字，所以你不需要做任何操作。

你可以涂黑第六张图的 \((1,3), (3,1), (5,3)\) 和 \((3,5)\) 来得到一个在 \((3,3)\) 的十字，这将花费你 \(4\) 分钟。

你可以涂黑第七张图的 \((1,2)\) 来得到一个在 \((4,2)\) 的十字。

你可以涂黑第八张图的 \((2,2)\) 来得到一个在 \((2,2)\) 的十字。当然，你也可以涂黑 \((1,3), (3,1)\) 和 \((3,3)\) 来得到一个在 \((3,3)\) 的十字，但这将花费你 \(3\) 分钟，并不是最优解。

第九张图你有九种最优解，其中一个十字在 \((1,1)\)：涂黑 \((1,2)\) 和 \((2,1)\)。

官方题解

作者 awoo

如果把每个格子当作十字的中心暴力访问每行每列，每个测试点的复杂度高达 \(O(nm(n+m))\) ，那就太慢了。但我们注意到每个格子 \((x,y)\) 都能被表示为 \(cnt_{row}[x]+cnt_{column}[y]-X\)（如果 \(a[x][y]\) 是白色，\(X\) 就是 \(1\)，否则是 \(0\)）。\(cnt_{row}[i]\) 表示第 \(i\) 行的白色格子数，而 \(cnt_{column}[i]\) 表示第 \(i\) 列的白色格子数，它们可以被预处理。

每个测试点的复杂度：\(O(nm)\)。

AC 代码

作者 岛田小雅

#include <bits/stdc++.h>
using namespace std;

const int N = 5e4+2;
int q, n, m;
string jz[N]; // 因为直接开char会爆炸，所以用string来存矩阵了
int cntrow[N], cntcolumn[N]; // 用来记录预处理的每行每列白色格子个数
int ans;

int main()
{
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> q;
    while(q--)
    {
        cin >> n >> m;
        for(int i = 1; i <= n; i++) jz[i].resize(m+1); // 框出需要用到的矩阵大小
        ans = n+m-1; // 初始化最大值
        for(int i = 1; i <= n; i++) cntrow[i] = 0;
        for(int i = 1; i <= m; i++) cntcolumn[i] =  0;
        
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= m; j++)
            {
                cin >> jz[i][j];
                if(jz[i][j] == '.') cntrow[i]++, cntcolumn[j]++;
            }
        }
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= m; j++)
            {
                int sum = cntrow[i]+cntcolumn[j];
                if(jz[i][j] == '.') sum--;
                ans = min(ans,sum); // 维护答案
            }
        }
        cout << ans << '\n';
    }
    return 0;
}